Дата__________ ФИ_____________________________________ Класс 10_____
Лабораторная работа № 1 по теме:
«ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛА ПО ОКРУЖНОСТИ ПОД ДЕЙСТВИЕМ СИЛ УПРУГОСТИ И ТЯЖЕСТИ».
Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности.
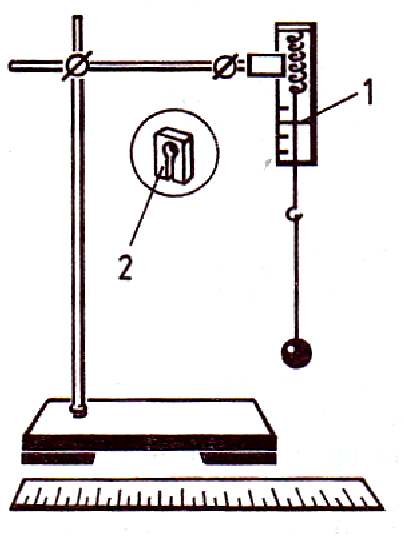
Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр
лабораторный, весы с разновесами, груз на нити, лист бумаги, линейка, пробка.
Теоретическая часть работы.
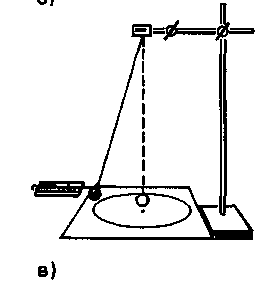
Э ксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса R. При этом нить АВ, к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести
ксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса R. При этом нить АВ, к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести 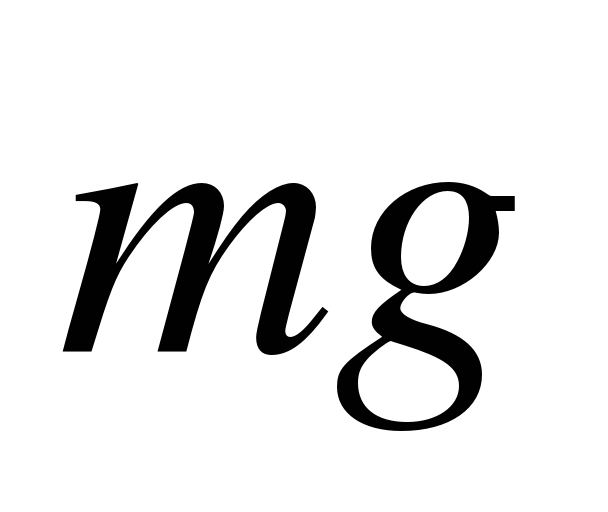 и натяжение нити
и натяжение нити  (рис. а). Они создают центростремительное ускорение
(рис. а). Они создают центростремительное ускорение 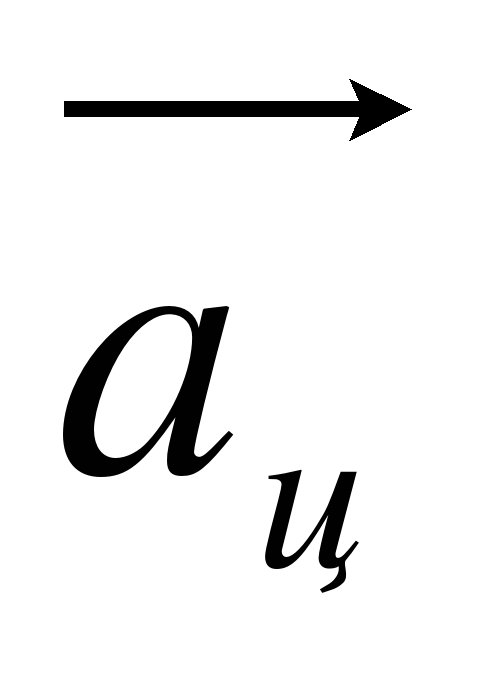 , направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:
, направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:
 .
.
Для определения ускорения надо измерить радиус окружности и период обращения шарика по окружности.
Центростремительное (нормальное) ускорение можно определить также, используя законы динамики.
Согласно второму закону Ньютона 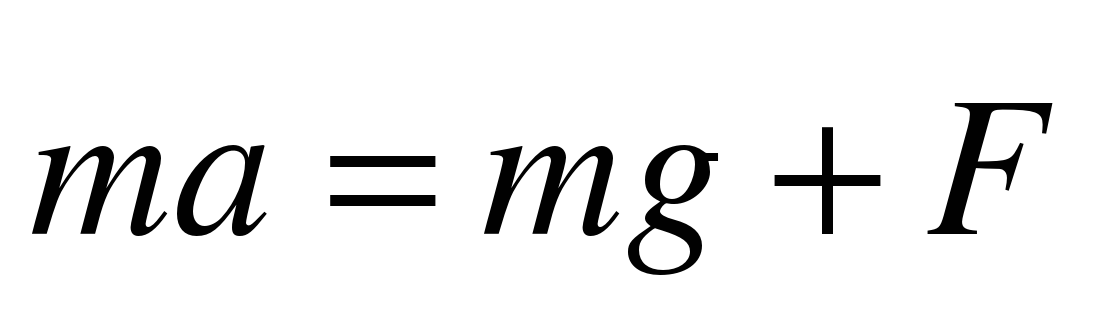 . Разложим силу
. Разложим силу  на составляющие
на составляющие  и
и  , направленные по радиусу к центру окружности и по вертикали вверх.
, направленные по радиусу к центру окружности и по вертикали вверх.
Тогда второй закон Ньютона запишется следующим образом:
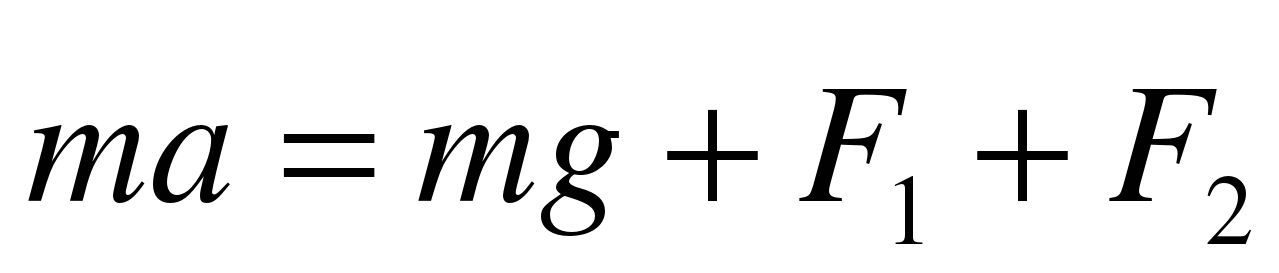
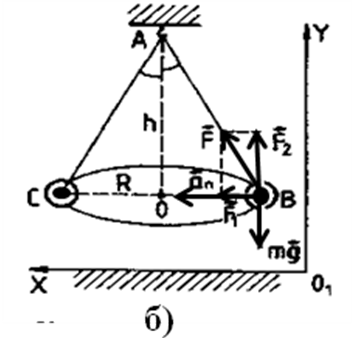 .
.
Направление координатных осей выберем так, как показано на рисунке б. В проекциях на ось О1у уравнение движения шарика примет вид: 0 = F2 — mg. Отсюда F2 = mg: составляющая  уравновешивает силу тяжести
уравновешивает силу тяжести 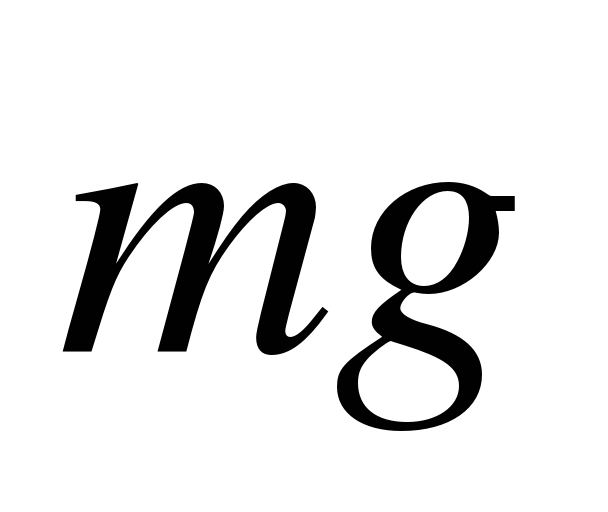 , действующую на шарик.
, действующую на шарик.
Запишем второй закон Ньютона в проекциях на ось О1х: man = F1. Отсюда 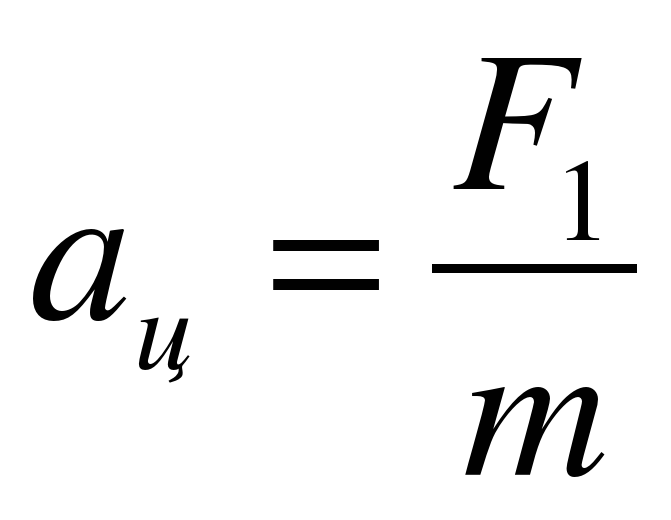 .
.
Модуль составляющей F1 можно определить различными способами. Во-первых, это можно сделать из подобия треугольников ОАВ и FBF1:
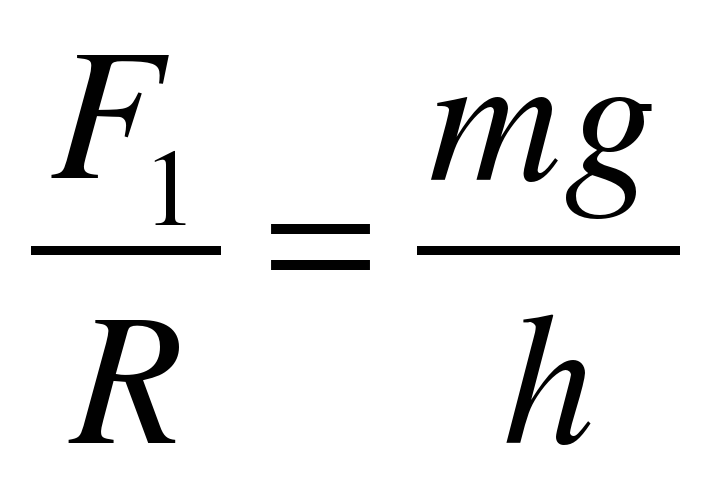
 .
.
Отсюда 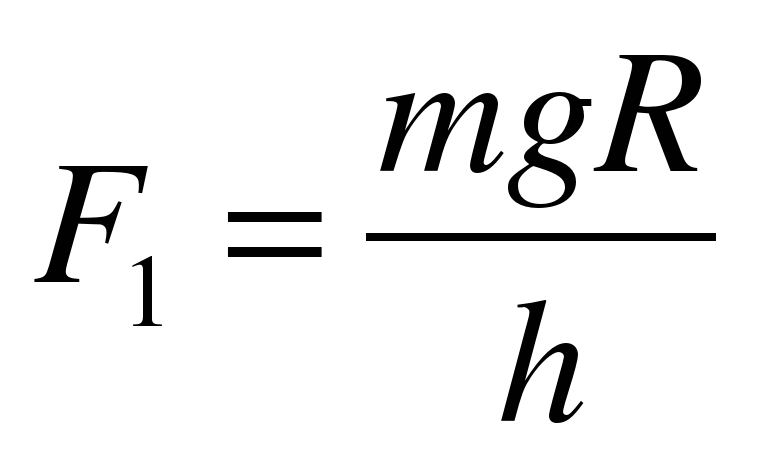 и
и 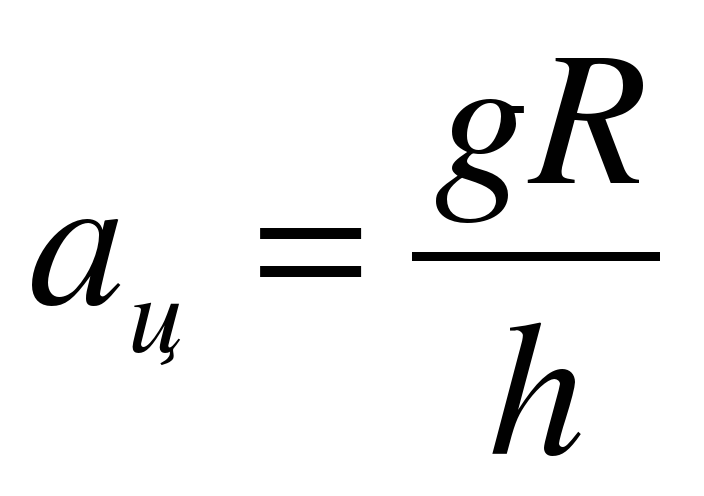 .
.
Во-вторых, модуль составляющей F1 можно непосредственно измерить динамометром. Для этого оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности (рис. в), и определяем показание динамометра. При этом сила упругости пружины уравновешивает составляющую  .
.
Сопоставим все три выражения для аn:
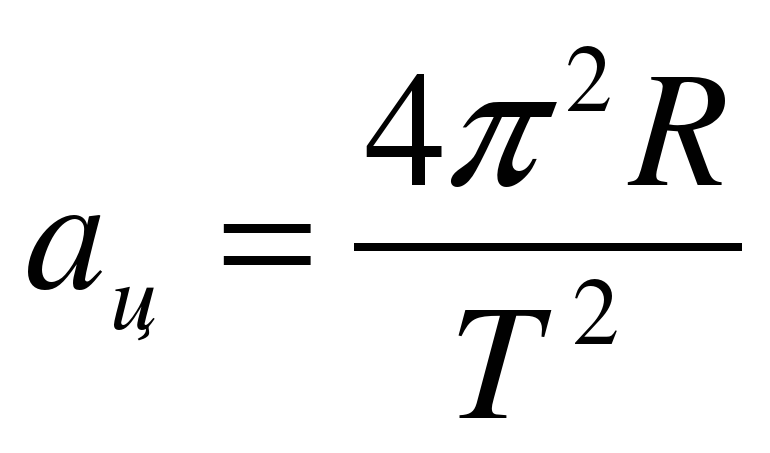 ,
, 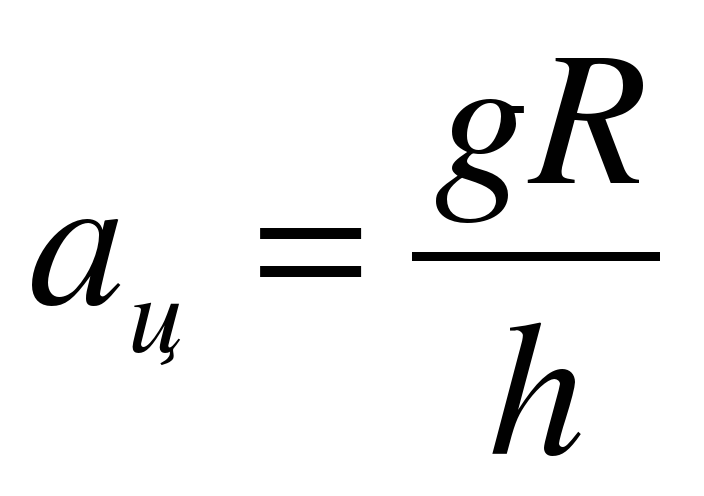 ,
, 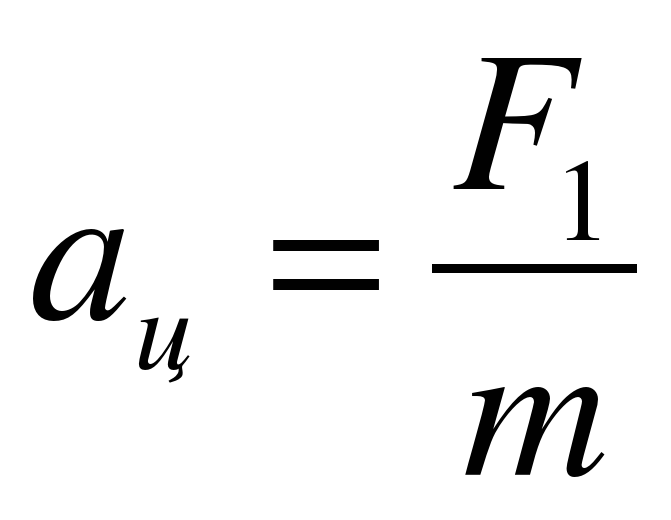 и убедимся, что они близки между собой.
и убедимся, что они близки между собой.
Ход работы.
1. Определите массу шарика на весах с точностью до 1 г.
2. Шарик, подвешенный на нити, закрепите в лапке штатива, используя кусок пробки.
3. Вычертите на листе бумаги окружность радиусом 20 см (R = 20 см = ________ м).
4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности.
5. Взяв нить пальцами у точки подвеса, приведите маятник во вращательное движение
над листом бумаги так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.
6. Отсчитываем время, за которое маятник совершает 50 полных оборотов (N = 50).
7. Рассчитайте период обращения маятника по формуле: T = t / N.
8. Рассчитайте значение центростремительного ускорения по формуле (1):
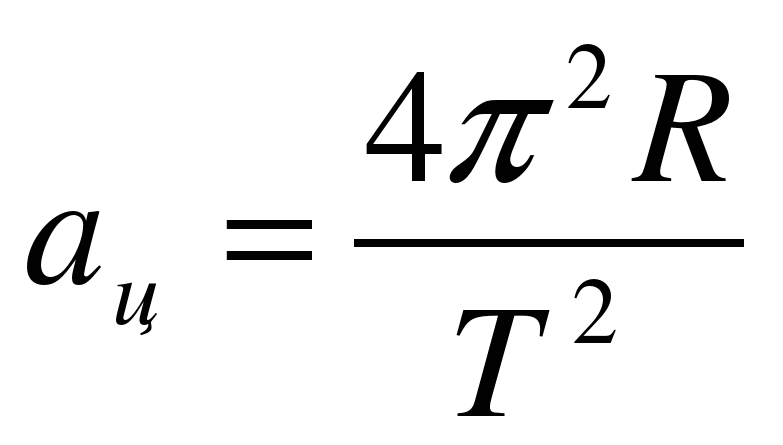
 =
=
9. Определите высоту конического маятника (h). Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса.
10. Рассчитайте значение центростремительное ускорение по формуле (2):
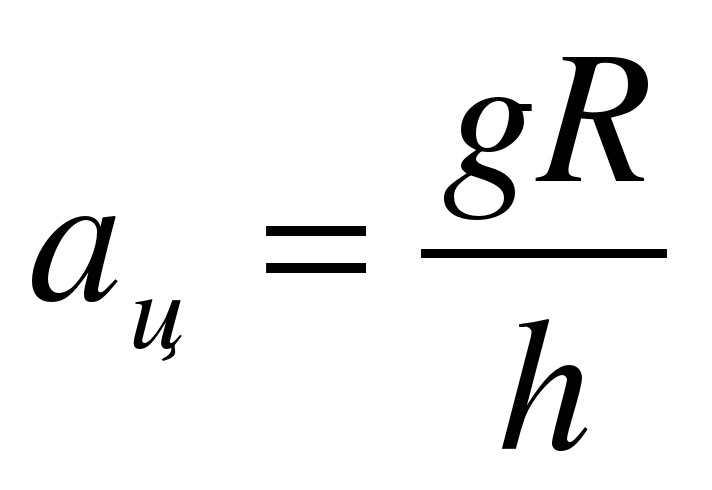
 =
=
11. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль составляющей  .
.
З атем вычисляем ускорение по формуле (3):
атем вычисляем ускорение по формуле (3):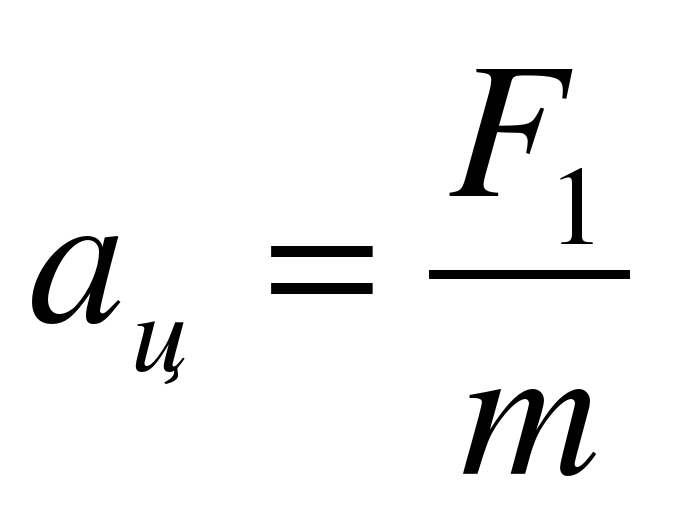 =
=
12. Результаты измерений и вычислений заносим в таблицу.
| Радиус окружности R, м | Число оборотов N | Время t, с | Период обращения T = t / N | Высота маятника h, м | Масса шарика m, кг | (1) Центр-ое ускорение м/с2 | (2) Центр-ое ускорение 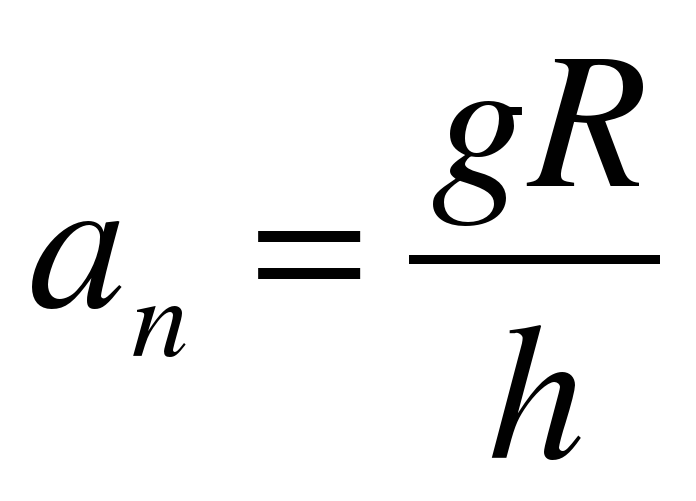 м/с2 | (3) Центр-ое ускорение 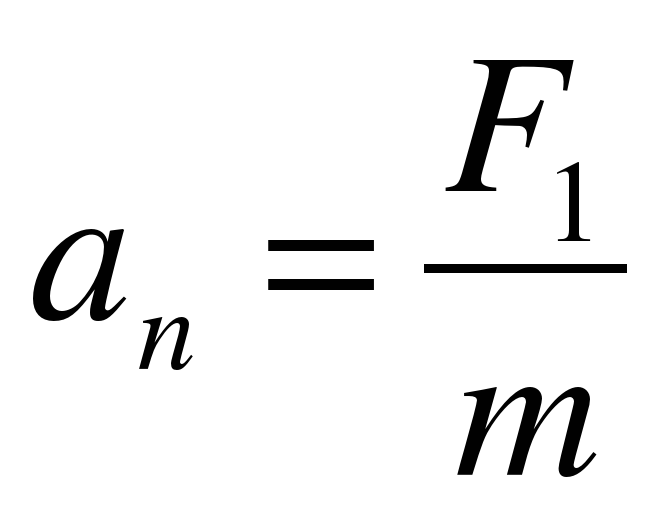 м/с2 |
|
|
| | | | | | | |
13. Сравните полученные три значения модуля центростремительного ускорения.
__________________________________________________________________________ ВЫВОД:
______________________________________________________________________________________________________________________________________________________________________________________________________________________________
Дополнительно:
Найдите относительную и абсолютную погрешность косвенного измерения ац (1) и (3):
Формула (1).  ________ ; Δац =
________ ; Δац = 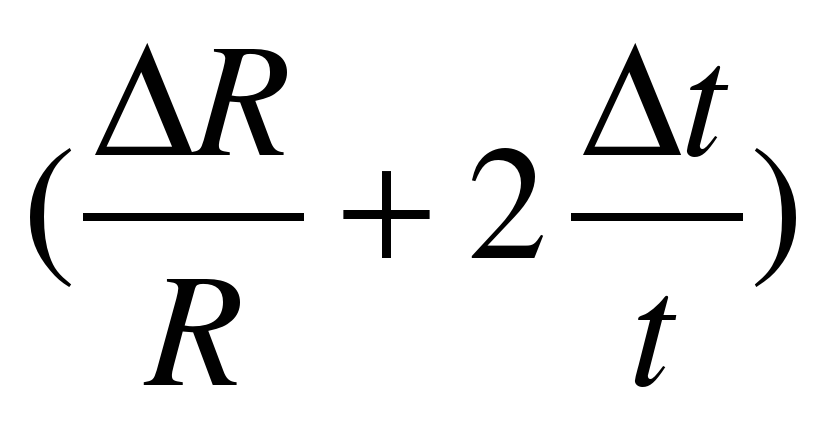 · ац = ________;
· ац = ________;
Формула (3). 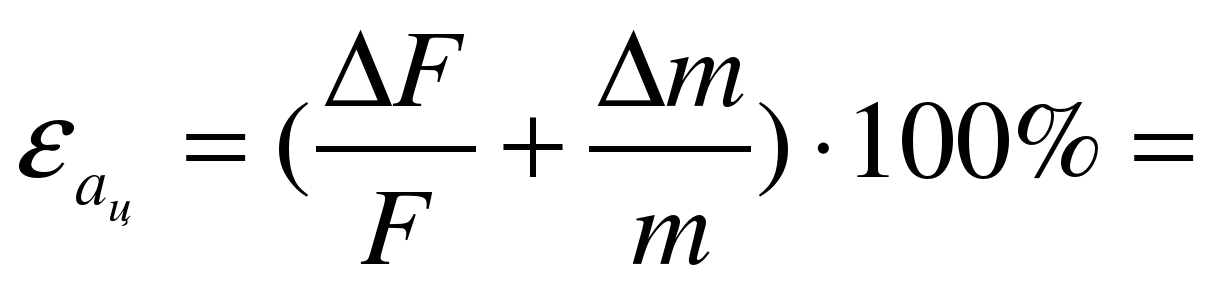 _________; Δац =
_________; Δац = 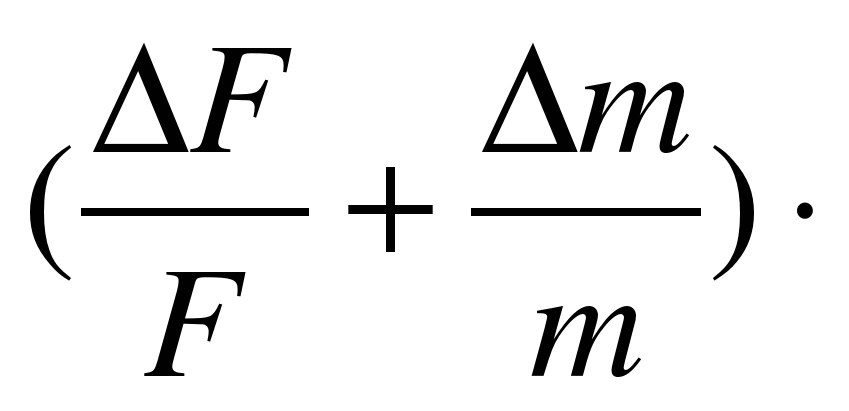 · ац = _______.
· ац = _______.
ОЦЕНКА _________







 ксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса
ксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса  .
. .
. =
=  =
=  атем вычисляем ускорение по формуле (3):
атем вычисляем ускорение по формуле (3):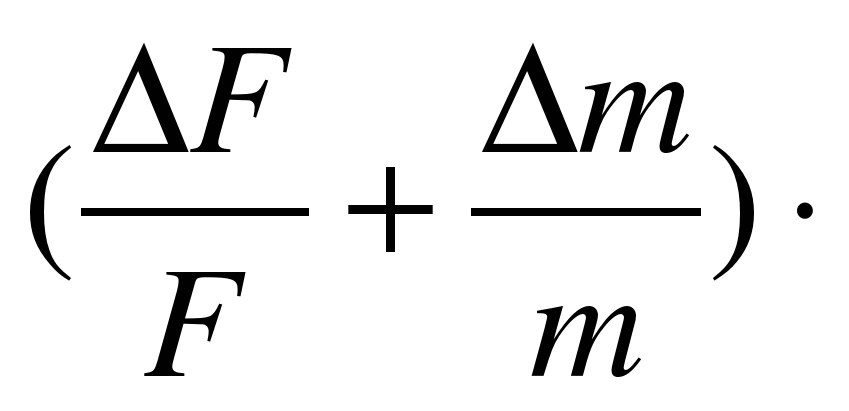 · ац = _______.
· ац = _______.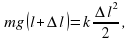

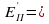 __________________________________________________________________
__________________________________________________________________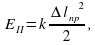 где
где 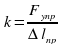 .
.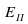 получим:
получим: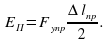
 __________________________________________________
__________________________________________________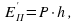
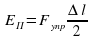 ,
,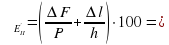 ___________;
___________; 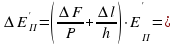 __________;
__________;  _________;
_________; 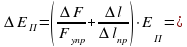 ________.
________. 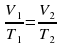 .
.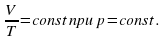
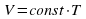 .
.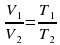 . Это можно осуществить. Используя в качестве газа воздух при атмосферном давлении.
. Это можно осуществить. Используя в качестве газа воздух при атмосферном давлении.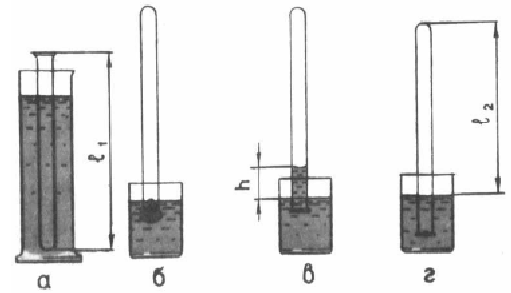
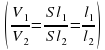 . Поэтому в работе следует сравнить отношения
. Поэтому в работе следует сравнить отношения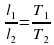 .
.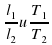 :
: 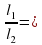 __________;
__________; 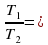 _____________.
_____________.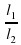
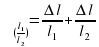 ,
, 
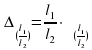
 ,
, 
 А
А ·
· ,
,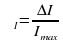 · 100%,
· 100%,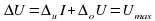 ·
·
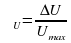 · 100%
· 100%

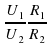

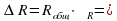

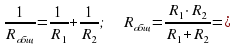
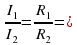
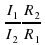

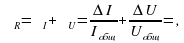
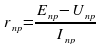 .
.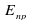 = __________.
= __________.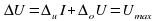 ·
·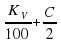
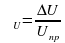 · 100%
· 100%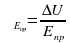 · 100%
· 100%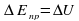
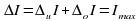 ·
·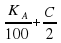
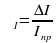 · 100%
· 100%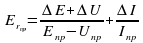
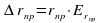
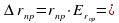 ______________________________________________________________________
______________________________________________________________________









