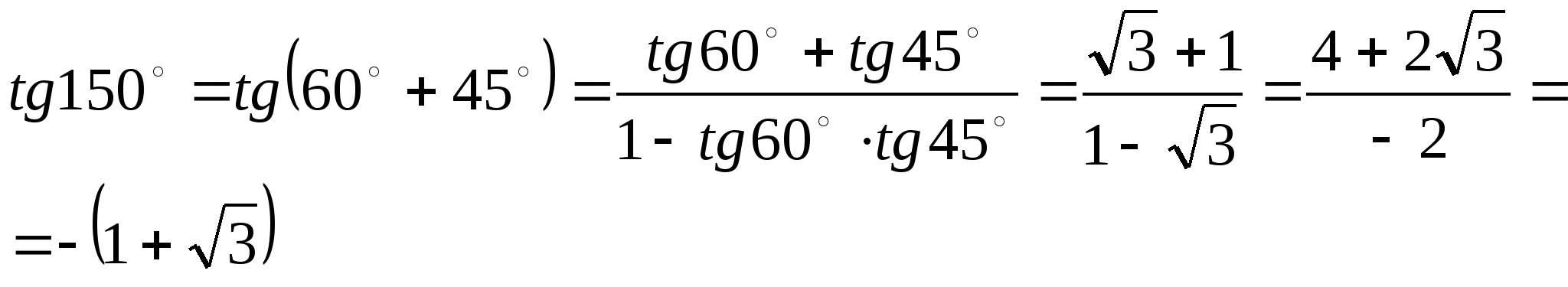Лекция по тригонометрии №2

Ф ормулы двойного угла

П ример:

Формулы сложения

1. sin (α + β) = sin α · cos β + sin β · cos α

2. sin (α - β) = sin α · cos β - sin β · cos α

3. cos (α + β) = cos α · cos β - sin α · sin β

4. cos (α - β) = cos α · cos β + sin α · sin β

5. tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)

6. tg (α - β) = (tg α - tgβ) ÷ (1 + tg α · tg β)

7. ctg (α + β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

8. ctg (α - β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)

Пример:

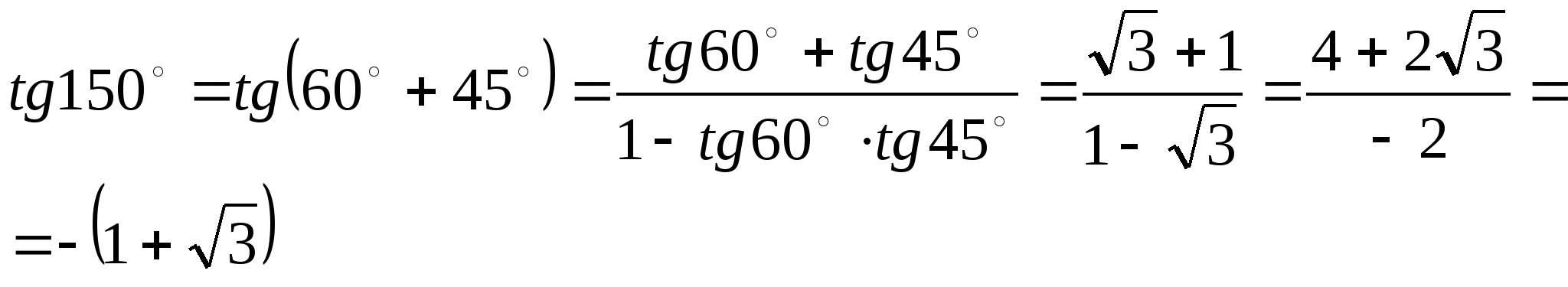
Формулы понижения степени

Формулы суммы и разности синусов и косинусов

Произведения тригонометрических функций

Тригонометрические функции половинного аргумента.

Рассмотрим следующие тождества:

  ,  , ,

Пример: 

Упростите выражение 

Используя формулу , получим  .

Для преобразования  используем формулу двойного угла 

Тогда 

Универсальная тригонометрическая подстановка:

Формулы приведения

Из прошлых тем нам известно, что тригонометрические функции являются периодичными функциями, именно поэтому при рассмотрении любых углов, их можно свести ко всем углам, находящимся на единичной окружности. Более того, любой угол можно свести к острому углу. Чтобы это сделать, необходимо знать формулы приведения.

Итак, давайте возьмем произвольный угол, который находится, например, в пределе от π до 3π/2. Данный угол можно записать следующим образом: (π + α). В данном случае α - острый угол. А теперь давайте определим, в какой четверти мы оказались. 

От π до 3π/2 - это третья четверть. В данной четверти и синус, и косинус имеет отрицательное значение. Для нахождения косинуса или синуса данного угла имеем право: cos(π + α) = -cos α. Полученное выражение называется одной из формул приведения. Данные уравнения можно получить для любой функции, в зависимости от знака данной четверти.

Формулы приведения

чтобы переходить от больших углов к острым совершенно не обязательно знать огромное множество формул приведений, достаточно понимать, как они были получены.

Для того, чтобы лучше понять, давайте рассмотри несколько примеров:

Итак, рассмотрим первый пример, описанный выше. Чтобы воспользоваться формулами приведения и прийти к острым углам, следует выделить π или 2 π. Чтобы не изменить величину аргумента, а также выделить π, необходимо от 180 отнять 30. Это означает, что в единичной окружности необходимо переместиться в точку π. Далее мы видим знак минус - это означает, что для того, чтобы отложить данный угол, следует двигаться по часовой стрелке, то есть от π отложить угол 30 градусов, или π/6. Мы оказались во второй четверти. Как мы уже знаем, величины углов во второй четверти являются положительными, так как здесь ордината принимает положительные значения. А это значит, что мы можем отбросить π и найти синус 30 градусов. Аналогичные вычисления можно сделать и с другими примерами.

Правило: Если в формуле приведения угол α вычитается из числа   или прибавляется к этому числу, взятому нечетное число раз, то приводимая функция меняется на кофункцию. Если же число   взято четное число раз, то название приводимой функции сохраняется. Знак перед приведенной функцией ставится такой, каков знак приводимой функции в соответствующей четверти, если считать угол α острый.

Закрепление знания алгоритмов решения задач на применение основных тригонометрических тождеств.

1 ) Найдите значение выражения

Мы видим, что  , поэтому либо разложим знаменатель по формуле косинуса двойного аргумента, либо, наоброт свернем числитель по той же формуле:

О твет: -24.

2) Найдите значение выражения 

Заметим, что 

Воспользеумся фомулой приведения:

Ответ: 5.

3) Найдите значение выражения 

Преобразуем аргументы тригонометрических функций в знаменателе дроби:

Вспомним, что   синус  - нечетная функция,  а косинус - четная:

А также периодичность синуса и косинуса. Получим:

С помощью тригонометрического круга определим значение

 и  : Получим: Ответ: - 16.