Четыре замечательные точки треугольника

Черноволова Е.В.

Севастопольский кадетский корпус Следственного комитета РФ им.В.И.Истомина

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

№ 664. Прямая АМ – касательная к окружности, АВ – хорда этой окружности. Докажите, что угол МАВ измеряется половиной дуги АВ, расположенной внутри угла МАВ.

М

В

А

О

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

2

142 0

Блиц-опрос. Найдите угол МАВ.

М

В

71 0

А

О

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

3

161 0

Блиц-опрос. Найдите угол МАВ.

М

В

161 0 : 2 = 160 0 60 / : 2

= 80 0 30 /

80 0 30 /

А

О

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

4

Блиц-опрос. Найдите дугу АВ.

В

= 172 0

172 0

86 0 2 =

О

86 0

М

А

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

5

Блиц-опрос. Найдите дугу АВ.

= 89 0 50 /

44 0 55 / 2 = 88 0 110 /

В

О

44 0 55 /

М

А

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

6

№ 670. Через точку А проведены касательные АВ

(В – точка касания) и секущая, которая пересекает окружность в точках Р и Q . Докажите, что АВ 2 = АР А Q .

А

Р

Р

Q

В

АВР А Q В

по 1 признаку подобия

АВ

АР

РВ

=

=

АВ 2 = АР А Q .

А Q

АВ

В Q

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

7

№ 671. Через точку А проведены касательные АВ

(В – точка касания) и секущая, которая пересекает окружность в точках С и D. Найдите С D , если АВ=4 см,

АС=2 см.

А

2

АВ 2 = А C А D .

2

C

?

6

4

4

4 2 = 2 А D .

D

А D = 8

В

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

8

№ 672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекает окружность в точках В 1 , С 1 , а другая – в точках В 2 , С 2 . Докажите, что АВ 1 АС 1 = АВ 2 АС 2

А

В 1

А D 2 = AB 1 А C 1

=

В 2

А D 2 = AB 2 А C 2

С 1

D

С 2

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

9

Четыре замечательные точки треугольника

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

п.74 Свойство биссектрисы угла

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

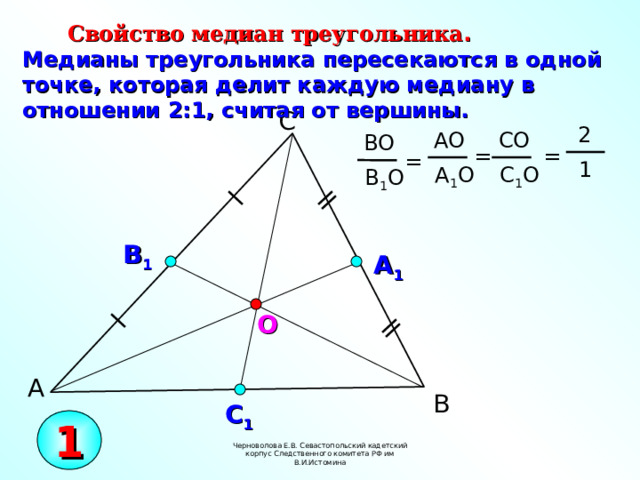
Свойство медиан треугольника .

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

С

2

СО

АО

ВО

=

=

=

1

А 1 О

С 1 О

В 1 О

В 1

А 1

О

А

В

С 1

1

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Теорема

В

K

А

1

2

М

L

С

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

13

Обратная теорема

Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

В

K

А

М

L

С

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

14

Следствие

Биссектрисы треугольника пересекаются в одной точке.

В

K

С1

А

По теореме

о биссектрисе

угла

О

ОМ

ОМ=ОК

ОК =О L

О L

В 1

А 1

М

L

=

По обратной теореме т. О лежит на биссектрисе угла С

2

С

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

15

п.75 Свойство серединного перпендикуляра к отрезку

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

Определение

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему.

М

С

В

a

Прямая a – серединный перпендикуляр к отрезку.

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

Теорема

Каждая точка серединного перпендикуляра

к отрезку равноудалена от концов этого отрезка.

М

O

B

A

m

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

18

Обратная теорема

Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

O

A

B

N

m

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

19

Следствие

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

n

C

B

О

По теореме о

серединном перпендикуляре к отрезку

р

m

О A

О A =О B

О C

О B =О C

=

A

По обратной теореме т. О лежит на сер. пер. к отрезку АС

3

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

20

п.76 Теорема о пересечении высот треугольника

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

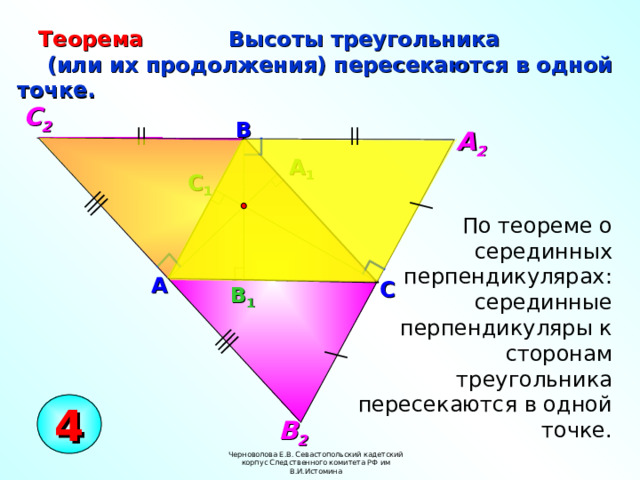
Теорема

Высоты треугольника

(или их продолжения) пересекаются в одной точке.

С 2

B

А 2

A 1

С 1

По теореме о серединных перпендикулярах: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

A

C

В 1

4

В 2

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

медиан

биссектрис

высот

перпенди

куляров

Замечательные точки треугольника.

Точка

пересечения

Точка

пересечения

Точка

пересечения

Точка

пересечения

серединных

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

23

Треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии!

Точка, обладающая таким свойством, называется

центром тяжести треугольника.

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

Высоты прямоугольного треугольника пересекаются в вершине С.

Высоты остроугольного треугольника пересекаются в точке О, которая лежит во внутренней области треугольника.

Точка пересечения

высот называется

ортоцентр.

O

В

М

Т

В

А

С

O

С

А

К

Высоты тупоугольного треугольника пересекаются

в точке О, которая лежит во внешней области треугольника.

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

O

Эта точка замечательная – точка пересечения биссектрис является центром вписанной окружности.

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина

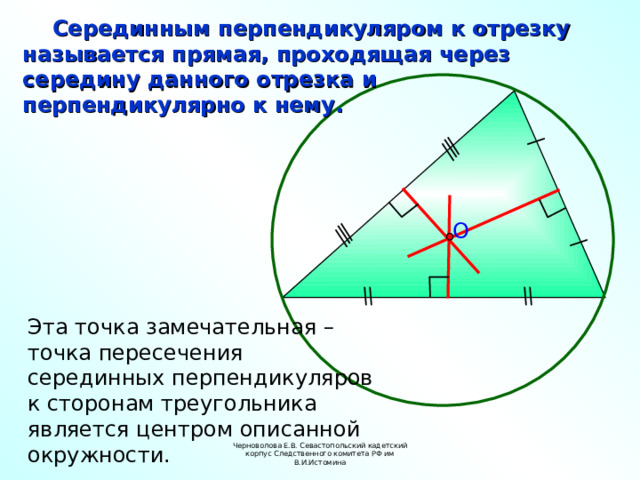
Серединным перпендикуляром к отрезку

называется прямая, проходящая через

середину данного отрезка и

перпендикулярно к нему.

O

Эта точка замечательная –

точка пересечения

серединных перпендикуляров

к сторонам треугольника

является центром описанной окружности.

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ им В.И.Истомина