ЕГЭ 2024 Декабрь Математика Вариант 4

РЕШУ ЕГЭ — математика профильная

Вариант № 79337488

1.  

i

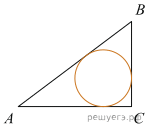Ка­те­ты рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка равны 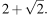Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в этот тре­уголь­ник.

2.  

i

Най­ди­те сумму ко­ор­ди­нат век­то­ра  +

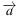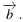
3.  

i

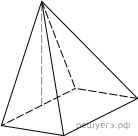Ос­но­ва­ни­ем пи­ра­ми­ды слу­жит пря­мо­уголь­ник, одна бо­ко­вая грань пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния, а три дру­гие бо­ко­вые грани на­кло­не­ны к плос­ко­сти ос­но­ва­ния под углом 60°. Вы­со­та пи­ра­ми­ды равна 6. Най­ди­те объем пи­ра­ми­ды.

4.  

i

В сред­нем из 1400 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 7 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

5.  

i

В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся кофе, равна 0,3. Ве­ро­ят­ность того, что кофе за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,12. Най­ди­те ве­ро­ят­ность того, что к концу дня кофе оста­нет­ся в обоих ав­то­ма­тах.

6.  

i

Ре­ши­те урав­не­ние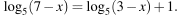

7.  

i

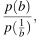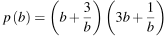Най­ди­те если при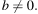

8.  

i

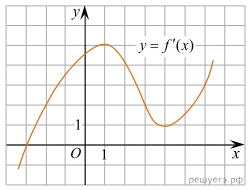На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции 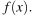Най­ди­те абс­цис­су точки, в ко­то­рой ка­са­тель­ная к гра­фи­ку 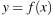па­рал­лель­на оси абс­цисс или сов­па­да­ет с ней.

9.  

i

Ско­рость ко­леб­лю­ще­го­ся на пру­жи­не груза ме­ня­ет­ся по за­ко­ну 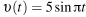(см/с), где t − время в се­кун­дах. Какую долю вре­ме­ни из пер­вой се­кун­ды ско­рость дви­же­ния была не менее 2,5 см/с? Ответ вы­ра­зи­те де­ся­тич­ной дро­бью, если нужно, округ­ли­те до сотых.

10.  

i

Изюм по­лу­ча­ет­ся в про­цес­се сушки ви­но­гра­да. Сколь­ко ки­ло­грам­мов ви­но­гра­да по­тре­бу­ет­ся для по­лу­че­ния 20 ки­ло­грам­мов изюма, если ви­но­град со­дер­жит 90% воды, а изюм со­дер­жит 5% воды?

11.  

i

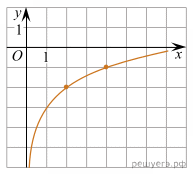На ри­сун­ке изоб­ражён гра­фик функ­ции 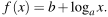Най­ди­те зна­че­ние x, при ко­то­ром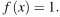

12.  

i

Най­ди­те точку мак­си­му­ма функ­ции

13.  

i

а)  Ре­ши­те урав­не­ние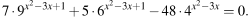

б)  Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку [−1; 2].

Ответ: а) 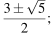б)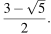

14.  

i

В пра­виль­ной четырёхуголь­ной пи­ра­ми­де PABCD сто­ро­на ос­но­ва­ния ABCD равна 12, бо­ко­вое ребро PA ― 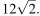Через вер­ши­ну A про­ве­де­на плос­кость α, пер­пен­ди­ку­ляр­ная пря­мой PC и пе­ре­се­ка­ю­щая ребро PC в точке K.

а)  До­ка­жи­те, что плос­кость α делит вы­со­ту PH пи­ра­ми­ды PABCD в от­но­ше­нии 2 : 1, счи­тая от вер­ши­ны P.

б)  Най­ди­те рас­сто­я­ние между пря­мы­ми PH и BK.

15.  

i

Ре­ши­те не­ра­вен­ство

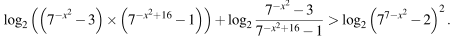
16.  

i

На каж­дом из двух за­во­дов ра­бо­та­ет по 100 че­ло­век. На пер­вом за­во­де один ра­бо­чий из­го­тав­ли­ва­ет за смену 3 де­та­ли А или 1 де­таль В. На вто­ром за­во­де для из­го­тов­ле­ния t де­та­лей (и А, и В) тре­бу­ет­ся t² че­ло­ве­ко-смен. Оба за­во­да по­став­ля­ют де­та­ли на ком­би­нат, где со­би­ра­ют из­де­лие, при­чем для его из­го­тов­ле­ния нужна 1 де­таль А и 3 де­та­ли В. При этом за­во­ды до­го­ва­ри­ва­ют­ся между собой из­го­тав­ли­вать де­та­ли так, чтобы можно было со­брать наи­боль­шее ко­ли­че­ство из­де­лий. Сколь­ко из­де­лий при таких усло­ви­ях может со­брать ком­би­нат за смену?

17.  

i

Окруж­ность с цен­тром O, рас­по­ло­жен­ном внут­ри пря­мо­уголь­ной тра­пе­ции ABCD, про­хо­дит через вер­ши­ны B и C боль­шей бо­ко­вой сто­ро­ны этой тра­пе­ции и ка­са­ет­ся бо­ко­вой сто­ро­ны AD в точке T.

а)  До­ка­жи­те, что угол BOC вдвое боль­ше угла BTC.

б)  Най­ди­те рас­сто­я­ние от точки T до пря­мой BC, если ос­но­ва­ния тра­пе­ции AB и CD равны 4 и 9 со­от­вет­ствен­но.

18.  

i

Най­ди­те все зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых си­сте­ма урав­не­ний

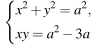
имеет ровно два раз­лич­ных ре­ше­ния?

19.  

i

Трое дру­зей иг­ра­ли в шашки. Один из них сыг­рал 25 игр, а дру­гой  — 17 игр. Мог ли тре­тий участ­ник сыг­рать  

а)  34;

б)  35;

в)  56 игр?