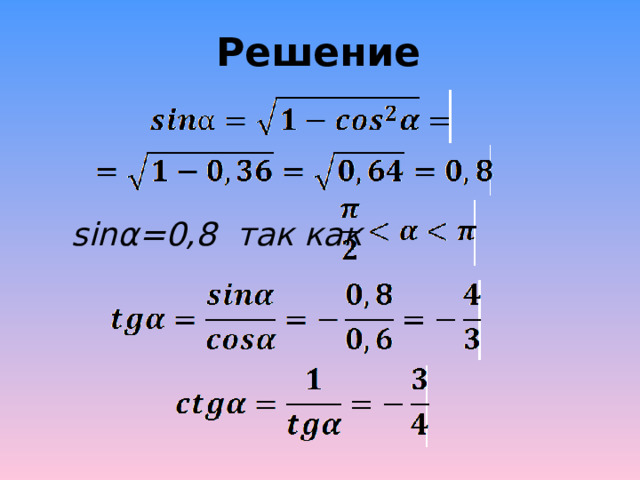Помогите мальчику выполнить домашнее задание, расставив между числами на дощечке знаки
+, —, ∙, ÷

Домашнее задание
sin(90°- α )+cos(180°+ α )+tg(270°+ α )+ctg(360°+ α )=
=cos α -cos α -ctg α +ctg α =0
sin( + α )-cos( α - 𝜋 )+tg( 𝜋- α )+ctg( - α )=
=cos α +cos α -tg α +ctg( - α )=2cos α -tg α +tg α =2cos α

Тема: Основное тригонометрическое тождество и следствия из него

Цель урока
установить зависимость между тригонометрическими функциями одного угла и научиться использовать ее при решении задач

План урока
- Организационный момент
- Актуализация ранее изученных знаний ( интеллектуальная разминка «Математическая мозаика»)
- Изучение нового материала
- Закрепление полученных знаний
- Подведение итогов занятия
- Рефлексия

Лист оценивания
Домашнее
задание
«Математическая мозаика»
Исследовательская работа
Решение задач по группам
Оценка за урок
Правильное выполнение приносит 1 балл
Если команда успешно справилась с заданием, то все члены команды получают 1 балл
Если команда успешно справилась с заданием, то все члены команды получают 1 балл
Тот, кто демонстрирует решение у доски получает 1 дополнительный балл
Если команда успешно справилась с заданием, то все члены команды получают 1 балл
Тот, кто демонстрирует решение у доски получает 1 дополнительный балл

Интеллектуальная разминка

«Математическая мозаика»
Вопросы
Ответы
Что называется синусом угла α?
Что называется косинусом
угла α?
Что называется тангенсом
угла α?
Что называется
котангенсом угла α?
В каких четвертях ?
I и IV четверти

В каких четвертях ?
III и IV четверти
В каких четвертях ?
Какой вид имеет уравнение окружности с центром в начале координат и радиуса R ?
В каких четвертях ?
II и IV четверти
I и III четверти
Какой знак имеет cosα в II четверти?
-

Аль-Батани
(850-929)
арабский ученый, внесший значительный вклад в развитие тригонометрии

Абу-ль-Вафа Мухамед-бен Мухамед
(940-998)
арабский ученый, составивший таблицы синусов и тангенсов через 10’ с точностью до 1/604.

Насиреддин Туси Мухамед
(1201-1274)
азербайджанский
астроном и математик

Бхаскара
(р. 1114, год смерти неизвестен)
индийский ученый

Евклид
Великий математик Древней Греции
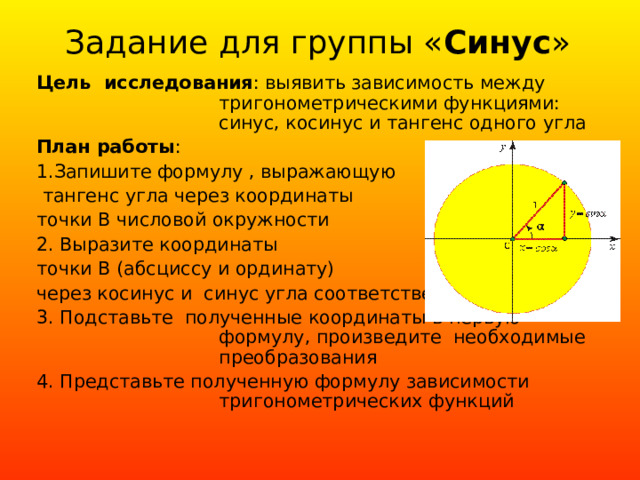
Задание для группы « C инус »
Цель исследования : выявить зависимость между тригонометрическими функциями: синус, косинус и тангенс одного угла
План работы :
1. Запишите формулу , выражающую
тангенс угла через координаты
точки В числовой окружности
2. Выразите координаты
точки В (абсциссу и ординату)
через косинус и синус угла соответственно
3. Подставьте полученные координаты в первую формулу, произведите необходимые преобразования
4. Представьте полученную формулу зависимости тригонометрических функций

Задание для группы « Тангенс »
Цель исследования : выявить зависимость между тригонометрическими функциями: синус, косинус и котангенс одного угла
План работы :
1. Запишите формулу , выражающую
котангенс угла через координаты
точки В числовой окружности
2. Выразите координаты
точки В (абсциссу и ординату)
через косинус и синус угла соответственно
3. Подставьте полученные координаты в первую формулу, произведите необходимые преобразования
4.Представьте полученную формулу зависимости тригонометрических функций
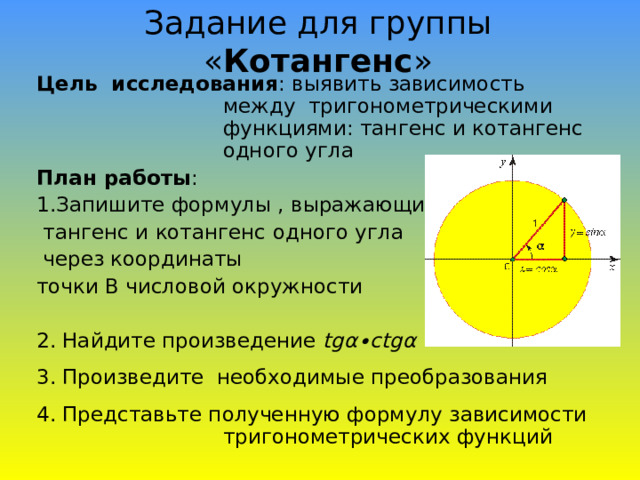
Задание для группы « Котангенс »
Цель исследования : выявить зависимость между тригонометрическими функциями: тангенс и котангенс одного угла
План работы :
1. Запишите формулы , выражающие
тангенс и котангенс одного угла
через координаты
точки В числовой окружности
2. Найдите произведение tg α∙ ctg α
3. Произведите необходимые преобразования
4. Представьте полученную формулу зависимости тригонометрических функций
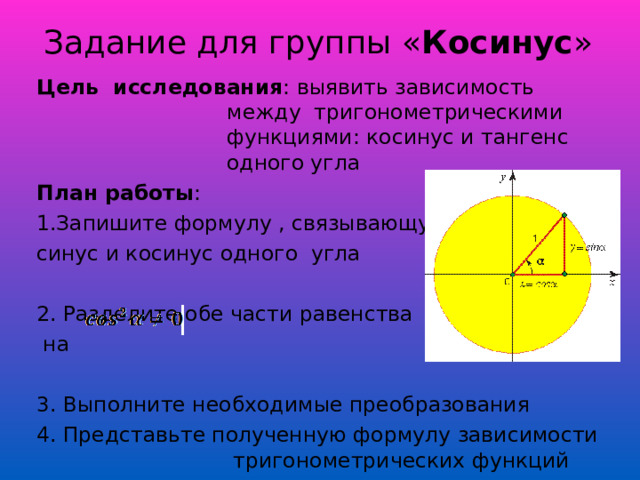
Задание для группы « Косинус »
Цель исследования : выявить зависимость между тригонометрическими функциями: косинус и тангенс одного угла
План работы :
1. Запишите формулу , связывающую
синус и косинус одного угла
2. Разделите обе части равенства
на
3. Выполните необходимые преобразования
4. Представьте полученную формулу зависимости тригонометрических функций

Задание для группы « Радиан »
Цель исследования : выявить зависимость между тригонометрическими функциями: синус и котангенс одного угла
План работы :
1. Запишите формулу , связывающую
синус и косинус одного угла
2. Разделите обе части равенства
на
3. Выполните необходимые преобразования
4. Представьте полученную формулу зависимости тригонометрических функций

Результат группы « C инус»
Формула, выражающая связь между тригонометрическими функциями тангенс, косинус и синус одного угла

Результат группы «Тангенс»
Формула, выражающая связь между тригонометрическими функциями котангенс, косинус и синус одного угла

Результат группы «Котангенс»
Формула, выражающая связь между тригонометрическими функциями котангенс и тангенс одного угла

Результат группы «Косинус»
Формула, выражающая связь между тригонометрическими функциями тангенс и косинус одного угла

Результат группы «Радиан»
Формула, выражающая связь между тригонометрическими функциями котангенс и синус одного угла

ЗАДАЧА
Найдите cos α , tg α и ctg α , если известно,
что и

ЗАДАНИЕ
Найдите значения тригонометрических функций
угла α , если известно, что
cos α =-0,6 и
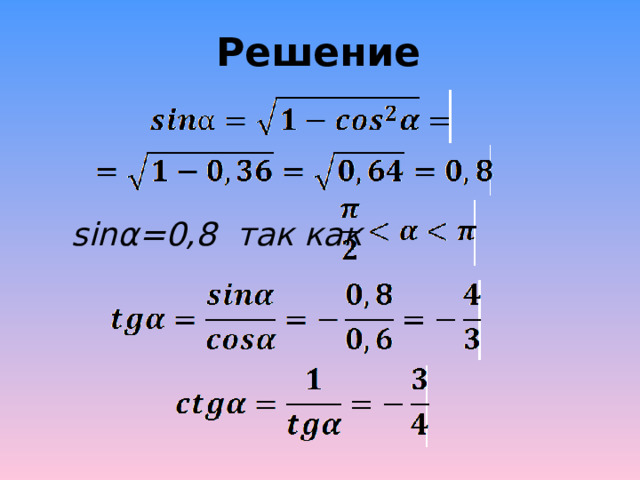
Решение
sin α =0,8 так как
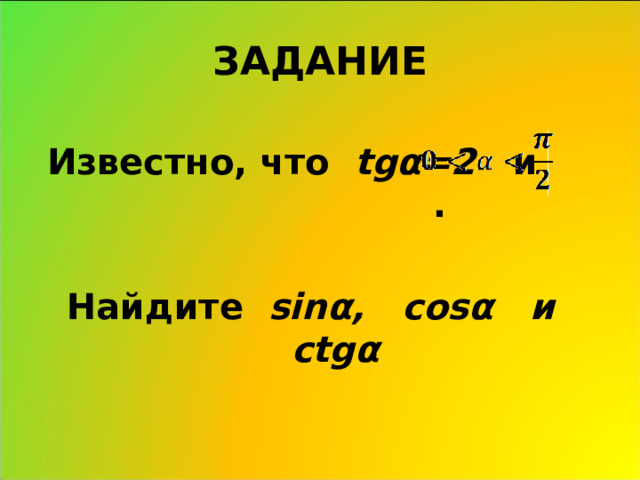
ЗАДАНИЕ
Известно, что tg α =2 и .
Найдите sin α , cos α и ctg α

РЕШЕНИЕ
Из формулы найдем,
что , отсюда
. Из формулы найдем,
что
Найдем .

Домашнее задание
Может ли для какого- нибудь угла β выполняться условие:
а)
б)

РЕФЛЕКСИЯ
- Что нового вы сегодня узнали?
- Чему вы сегодня научились?
- Что вам сегодня больше всего запомнилось на занятии?
- Что понравилось?