Кыргызстан, Бишкек
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 28.03.2025 13:03
Нуруева Жаңыл Болотовна
Преподаватель математики
53 года
13 500
2 818 
Местоположение
Специализация
Логарифмическая функция
Категория:
Алгебра
29.04.2020 22:09
Просмотр содержимого документа
«Логарифмическая функция»
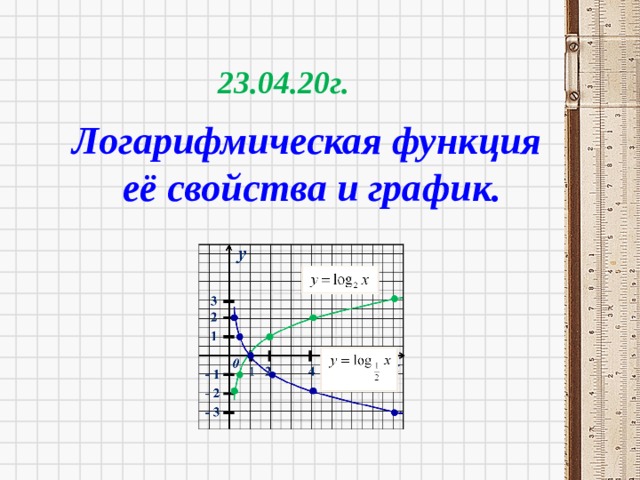
23.04.20г.
Логарифмическая функция
её свойства и график.
Устная работа
Вычисли
log 9 81=
log 4 16=
log 0.2 5=
log 9 1=
log 9 9=
log 0.3 0.0081=
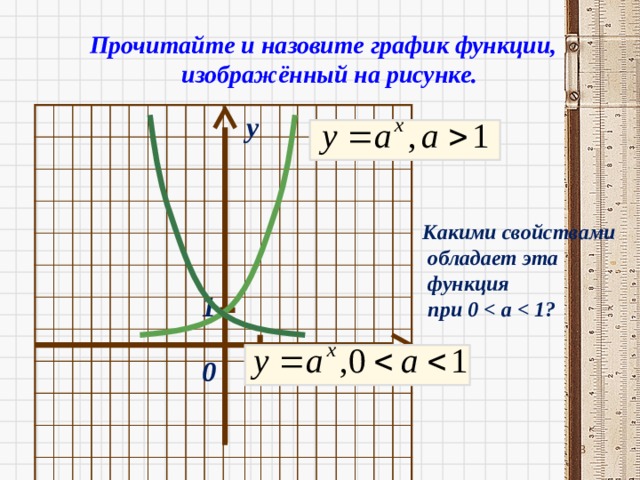
Прочитайте и назовите график функции,
изображённый на рисунке.
y
Какими свойствами
обладает эта
функция
при 0
1
1
0
x
План прочтения графика:
1) D(f) – область определения функции .
2) Чётность или нечётность функции .
3) Промежутки возрастания, убывания функции .
4) Ограниченность функции .
5) Наибольшие, наименьшие значения функции .
6) Непрерывность функции.
7) E(f) – область значений функции.
8) Выпуклость функции.
Что представляют собой представленные выражения?
Решите показательные уравнения с помощью выражения переменной через переменную
0 , ≠1 " width="640"
Логарифмическая функция
у = log а x
– заданное число, 0 , ≠1
0, a (a-положительное число, не равное 1) " width="640"
Определение
Функция заданную формулой
называют логарифмической функцией с основанием a
(a0, a
(a-положительное число, не равное 1)
x
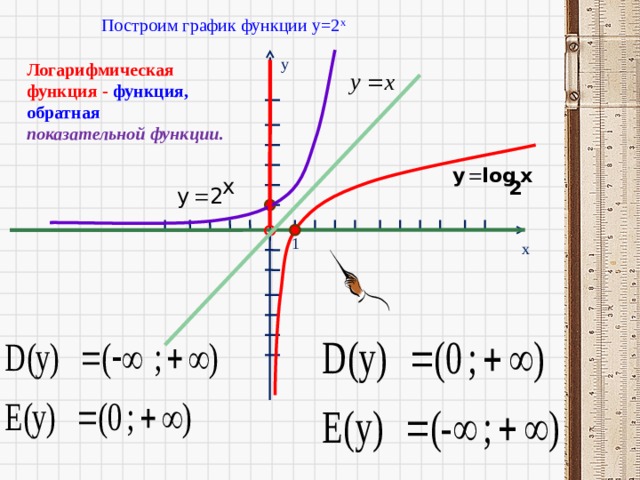
Построим график функции y=2 x
y
Логарифмическая функция - функция, обратная показательной функции .
1
x
Построим график функции y=(0.5) x
y
1
x
x
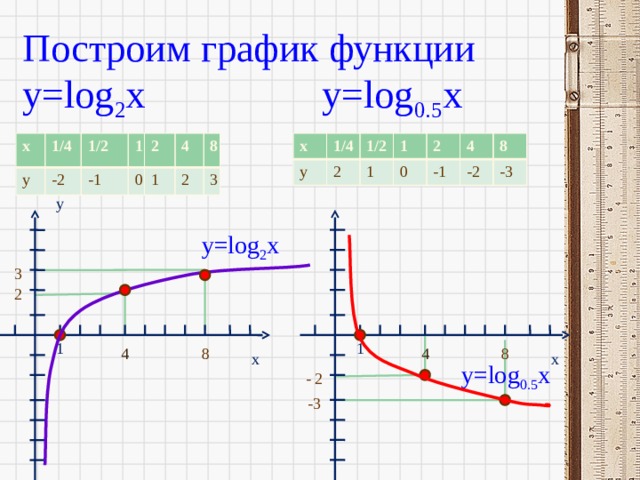
Построим график функции y=log 2 x y=log 0.5 x
x
x
1/4
1/4
y
y
2
-2
1/2
1/2
1
1
-1
1
0
0
2
2
4
4
1
-1
8
2
-2
8
3
-3
y
y=log 2 x
3
2
1
1
8
4
8
4
y=log 0.5 x
- 2
-3
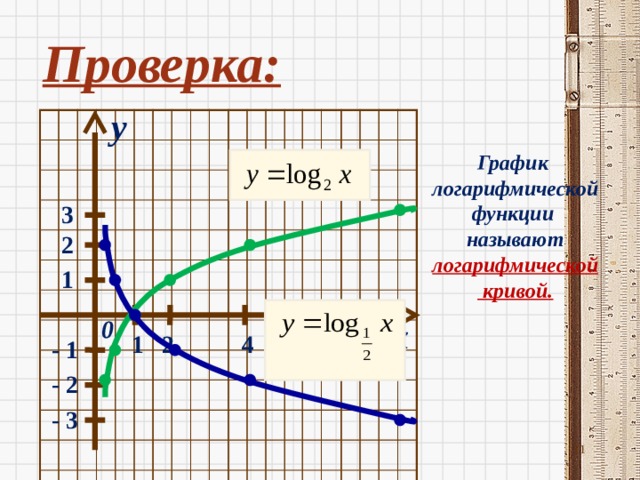
Проверка:
y
График
логарифмической
функции
называют
логарифмической
кривой.
3
2
1
x
0
1
4
2
8
- 1
- 2
- 3
1. у 1) D(f) = (0, + ∞) ; 2) не является ни чётной, ни нечётной; х 0 3) возрастает на (0, + ∞) ; 4)не ограничена сверху, не ограничена снизу; 5)не имеет ни наибольшего, ни наименьшего значений; 6) непрерывна; 7) E(f) = (- ∞ , + ∞) ; 8) выпукла вверх. 12 " width="640"
Свойства функции у = log a x, a 1.
у
1) D(f) = (0, + ∞) ;
2) не является ни чётной,
ни нечётной;
х
0
3) возрастает на (0, + ∞) ;
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞ , + ∞) ;
8) выпукла вверх.
12
Свойства функции у = log a x, 0
у
1) D(f) = (0, + ∞) ;
2) не является ни чётной,
ни нечётной;
х
0
3) убывает на (0, + ∞) ;
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞ , + ∞) ;
8) выпукла вниз.
13
1 4) не ограничена ни сверху, ни снизу 1) D(F):(0;+∞) 2) не является ни четной, ни нечетной 5) не имеет ни наибольшего, ни наименьшего значений 3) возрастает на своей области определения 6) непрерывна 4) не ограничена ни сверху, ни снизу 7) E(F):(- ∞;+ ∞) 8) выпукла вниз 5) не имеет ни наибольшего, ни наименьшего значений 6) непрерывна 7) E(F):(- ∞;+ ∞) 8 ) выпукла вверх y x x y=log a x 0 a y=log a x a1 " width="640"
Свойства функции
y
Свойства функции y=log a x, при 0
1) D(F):(0;+∞)
2) не является ни четной, ни нечетной
3) убывает на своей области определения
Свойства функции y=log a x, при a1
4) не ограничена ни сверху, ни снизу
1) D(F):(0;+∞)
2) не является ни четной, ни нечетной
5) не имеет ни наибольшего, ни наименьшего значений
3) возрастает на своей области определения
6) непрерывна
4) не ограничена ни сверху, ни снизу
7) E(F):(- ∞;+ ∞)
8) выпукла вниз
5) не имеет ни наибольшего, ни наименьшего значений
6) непрерывна
7) E(F):(- ∞;+ ∞)
8 ) выпукла вверх
y
x
x
y=log a x 0 a
y=log a x a1
1 1 0 D(f) = (0, + ∞) 2 не является ни чётной, ни нечётной; 3 возрастает на (0, + ∞) 4 не ограничена сверху, не ограничена снизу убывает на (0, + ∞) 5 не имеет ни наибольшего, ни наименьшего значений 6 непрерывна 7 E(f) = (- ∞ , + ∞) 8 выпукла вверх выпукла вниз " width="640"
Основные свойства логарифмической
функции
№
a 1
1
0
D(f) = (0, + ∞)
2
не является ни чётной, ни нечётной;
3
возрастает на (0, + ∞)
4
не ограничена сверху, не ограничена снизу
убывает на (0, + ∞)
5
не имеет ни наибольшего, ни наименьшего значений
6
непрерывна
7
E(f) = (- ∞ , + ∞)
8
выпукла вверх
выпукла вниз
499
Найдите область определения выражения:
б)
а)
в)
г)
Найдите область определения выражения:
500
б)
а)
г)
в)
* 3 2 1 0 -1 -2 -3 у = х 1 2 3 4 5 6 7 8 9 № 323. Найти приближенное значение. * " width="640"
y
*
3
2
1
0
-1
-2
-3
у =
х
1 2 3 4 5 6 7 8 9
№ 323. Найти приближенное значение.
*
у = log 3 x . 2 23 1 0 у = x . 3 у = x . 1 " width="640"
1
Сравните числа:
1
у = log 3 x .
2
23
1
0
у = x .
3
у = x .
1
501
Сравните числа:
а) и
б) и
502
а) и
б) и
504
у =
б)
а)
у =
9
3
x
1
x
1
3
9
у
-2
-1
2
1
0
у
2
1
-2
-1
0
у
у
4
3
4
3
у =
у =
2
1
2
1
х
х
-2 -1
0 1 2 3 4 5 6 7 8 9
-2 -1
0 1 2 3 4 5 6 7 8 9
-1
-2
-1
-2
-3
-3
Найдите значение выражения :
505
г)
а)
508
Решите уравнение:
а)
Ответ:
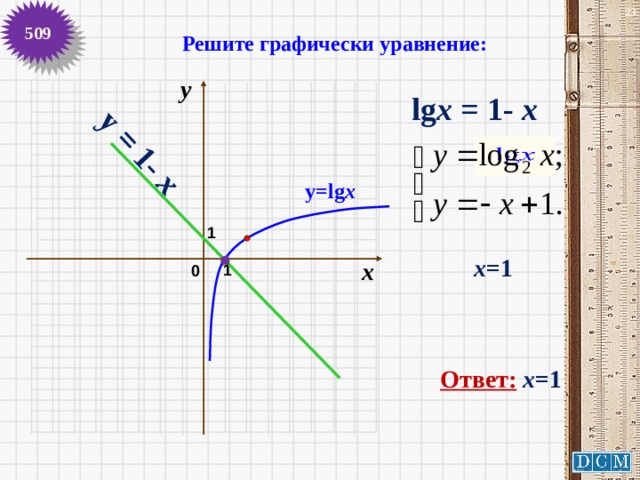
509
y = 1- x
Решите графически уравнение:
у
lg x = 1- x
у=lg x
1
х =1
х
1
0
Ответ: х =1
21
509
Решите графически уравнение :
у
у= 2 х- 5
у= 2х -5
1
х
1
0
2,5
0
х
0
-5
у
№ 333. Задание с ошибкой. Предлагаю просмотреть решение. После обнаружения ошибки, приглашаю к доске ученика оформить верное решение.
у= x
х =2
Ответ: х =2
![511 Найдите наибольшее и наименьшее значения функции у =log 2 x на промежутке [0,5; 4] у -1 y (0,5) = у =log 2 x у (4) = 2 1 0,5 4 х 1 0 25](https://fsd.multiurok.ru/html/2020/04/29/s_5ea9d0dfb390e/img24.jpg)
511
Найдите наибольшее и наименьшее значения функции
у =log 2 x на промежутке [0,5; 4]
у
-1
y (0,5) =
у =log 2 x
у (4) =
2
1
0,5
4
х
1
0
25
1. Найдите область определения функции:
Ответы
1) у = log 0,3 х
2) у = log 2 (х-1)
3) у = log 3 (3-х)
(0; +∞)
(1;+∞)
(-∞; 3)
3. Какие из функций являются возрастающими?
а) у = log 5 х
б)
в) у = log π х
г)
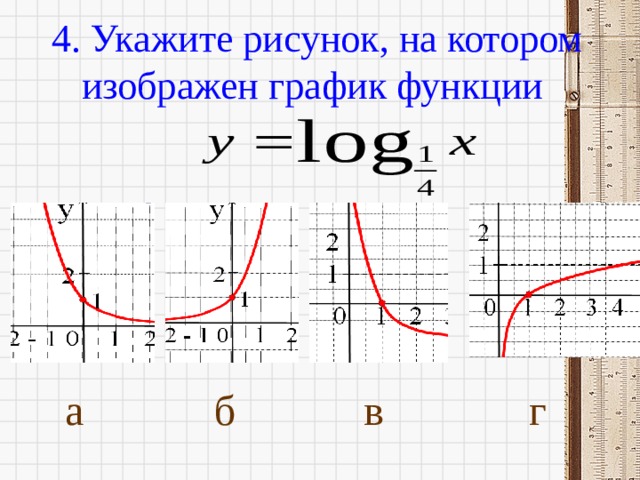
4. Укажите рисунок, на котором изображен график функции
б
в
г
а
Задание №1
Найдите наибольшее и наименьшее значения
функции на промежутке:
у
у
х
х
Функция возрастает,
значит: y наим. = lg1 = 0
y наиб. = lg1000 = lg10 ³ = 3
Функция убывает,
значит: y наим. = -3
y наиб. = 2
29
Рефлексия
- О чем вы не имели представления до сегодняшнего урока, и что теперь вам стало ясно?
- Что нового вы узнали о логарифмической функции и ее приложениях?
- С какими трудностями вы столкнулись при выполнении заданий?
- Выделите тот вопрос, который для вас оказался менее понятным.
- Какая информация вас заинтересовала?
- Составьте синквейн «логарифмическая функция»
Домашнее задание
Удачи!!!!!
§ 10. пункт-38
№ 501-511
31
Это интересно
Известно завещание знаменитого американского государственного деятеля Бенджамина Франклина. Вот отрывок из него: «Препоручаю 1000 фунтов стерлингов бостонским жителям. Если они примут эту тысячу фунтов, то должны поручить ее отборнейшим гражданам, а они будут давать их с процентами, по 5 на сто в год, в заем молодым ремесленникам. Сумма эта через сто лет возвысится до 131000 фунтов стерлингов. Я желаю тогда 100000 фунтов были употреблены на постройку общественных зданий, остальные же 31000 фунтов отданы в проценты на 100 лет…». Оставляя всего 1000 фунтов, Франклин распределяет миллионы. Математический расчет это подтверждает
Вычисления с помощью логарифма
31
Логарифми́ческая
счётная
лине́йка
линейка
аналоговое вычислительное устройство , позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб), вычисление квадратных и кубических корней, вычисление логарифмов , потенцирование , вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени.
До появления карманных калькуляторов этот инструмент служил незаменимым расчётным орудием инженера. Точность расчётов — около 3 значащих цифр.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
