
Логические основы обработки информации
Автор презентации :
Волков Ю.П., учитель информатики и ИКТ МБОУ СОШ №11 г. Струнино Владимирской обл.

Логические переменные
В алгебре логики высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения:
Истина Ложь
1 0
True False

Базовые логические операции

Конъюнкция (логическое умножение)
A Λ B
A
B
0
A Λ B
0
0
1
1
0
0
1
0
1
0
1
А и B
A and B
A & B
A Λ B
A * B
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

Дизъюнкция (логическое сложение)
A v B
A
B
0
A v B
0
0
1
0
1
1
0
1
1
1
1
А или B
A or B
A | B
A v B
A + B
Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда и только тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
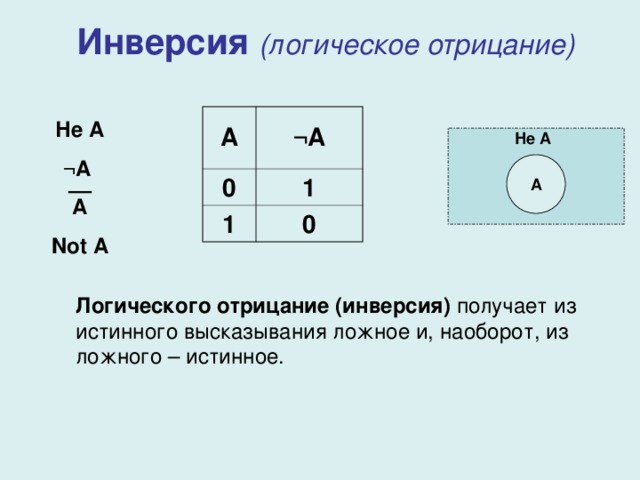
Инверсия (логическое отрицание)
A
¬A
0
1
1
0
Не А
¬A
A
Not A
Не А
А
Логического отрицание (инверсия) получает из истинного высказывания ложное и, наоборот, из ложного – истинное.

Логические выражения
Запишем в форме логического выражения составное высказывание:
(2 × 2 = 5 или 2 × 2 = 4) и (2 × 2 ≠ 5 или 2 × 2 ≠ 4)
A = «2 × 2=5» – ложно (0)
В = «2 × 2=4» – истинно (1)
( A v B) Λ ( ¬A v ¬B )
Определить истинность логического высказывания:
( A v B) Λ ( ¬A v ¬B ) = (0 v 1 ) Λ ( 1 v 0 ) = 1
Приоритет операций:
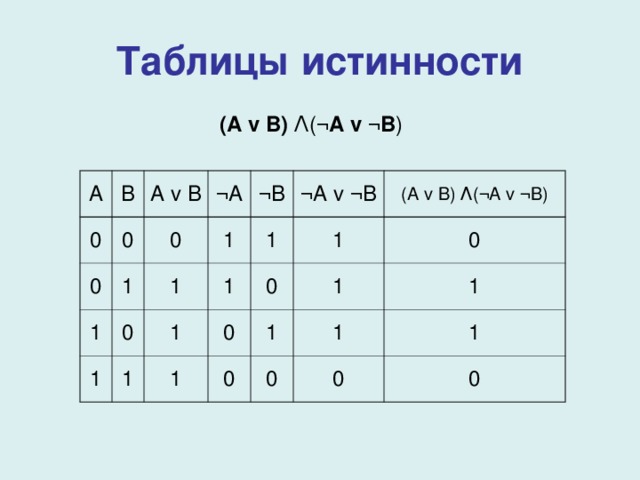
Таблицы истинности
( A v B) Λ ( ¬A v ¬B )
A
B
0
0
A v B
0
¬A
1
1
0
1
0
1
¬B
1
1
¬A v ¬B
1
1
1
0
0
( A v B) Λ (¬A v ¬B)
1
1
1
0
0
1
1
1
0
0
1
0

Равносильные логические выражения
Логические выражения, у которых таблицы истинности совпадают, называются равносильными .
¬ ( A v B )
¬A Λ ¬B
A
0
B
A
B
0
0
0
A v B
1
0
¬ ( A v B )
1
0
¬A
0
1
0
1
¬B
1
1
1
1
1
¬A Λ ¬B
0
1
1
0
1
1
0
0
1
1
1
0
0
0
1
0
0
0
0
¬A Λ ¬B = ¬ ( A v B )
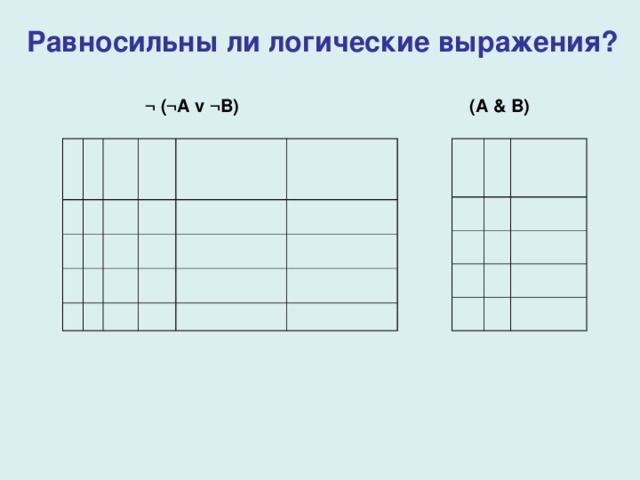
Равносильны ли логические выражения?
¬ (¬A v ¬B) (A & B)

Закрепление изученного материала
Саша старше Маши и Маша старше Коли или Саши
- Записать данное выражение используя логические переменные
- Построить таблицу истинности для данного логического выражения
- Какому известному выражению равносильно данное выражение
- Определить старшинство Саши, Маши и Коли
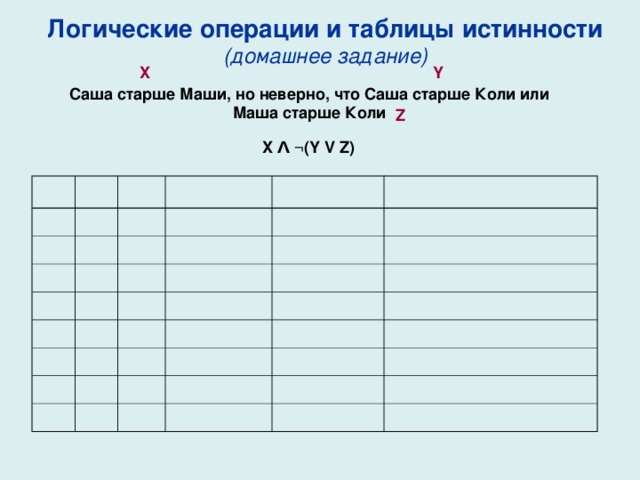
Логические операции и таблицы истинности (домашнее задание)
X
Y
Саша старше Маши, но неверно, что Саша старше Коли или Маша старше Коли
Z
X Λ ¬(Y V Z)

Закрепление изученного материала
Построив таблицы истинности, определите, равносильны ли выражения?
- A V (B Λ C) (A V B) Λ (A V C)
- A V B Λ C (A Λ C) V (B Λ C)

Логические операции

Строгая дизъюнкция
A v B
A
B
0
0
A v B
0
1
0
1
0
1
1
1
1
0
или А, или B
A xor B
A v B
A B
+
Составное высказывание, образованное с помощью строгой дизъюнкции, истинно тогда, когда истинно только одно из входящих в него простых высказываний.
A v B = ( A v B) Λ (¬A v ¬B)
A v B = A Λ ¬B v ¬A Λ B

Импликация
А В
A
B
0
A B
0
0
1
1
1
1
0
1
1
0
1
А В
А В
если А, то B
A imp B
A B
В А
А В
А В
А В
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки следует ложный вывод.
A B = ¬A v B

Эквивалентность
А тогда и только тогда, когда B
A eqv B
A B
A ~ B
A ≡ B
A
B
0
A ~ B
0
0
1
1
1
0
1
0
1
0
1
А ~ В
А В
А В
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
A ~ B = ( A v ¬ B) Λ (¬A v B)
A ~ B = A Λ B v ¬A Λ ¬B

Приоритет операций
Инверсия ¬
Конъюнкция Λ
Дизъюнкция v
Строгая дизъюнкция v
Импликация
Эквивалентность ~
Равенство (равносильность)

Решение задач
Записать в виде логической формулы высказывание и определить его истинность: «Если Иванов здоров и богат, то он здоров»
A Λ B → A
A
B
0
A Λ B
0
0
A Λ B → A
1
1
0
1
0
1
0
0
1
1
1
1
1

Решение задач
Определить значение (истинность) выражений:
((a ν ¬b) → b) ^ (¬a ν b)
¬ ( a ^ b) ≡ ¬ a ν b
A ^ (B ^ ¬ B → ¬ C)
A ν (B ν ¬ B → ¬ C)
((С ν B ) → B) ^ (A ^ B) → B
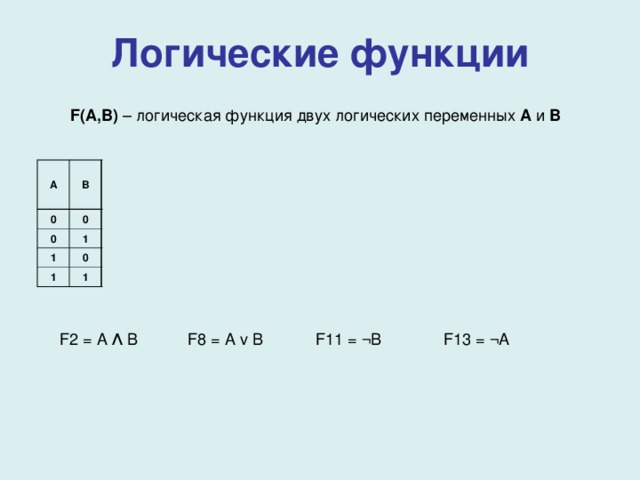
Логические функции
F(A,B) – логическая функция двух логических переменных A и B
A
B
0
0
0
F1
F2
1
0
1
0
0
0
F3
1
1
0
0
F4
0
0
0
F5
0
0
0
F6
0
1
1
0
1
1
F7
0
1
0
F8
1
0
0
F9
1
0
0
1
1
1
F10
1
1
0
0
F11
1
1
0
F12
1
0
1
0
F13
0
0
0
1
F14
1
1
1
1
0
F15
1
1
1
F16
1
0
1
1
0
0
1
1
1
1
0
1
F2 = A Λ B F8 = A v B F11 = ¬B F13 = ¬A
 3) → (X 4)) Для какого из указанных значений X ложно высказывание: ((X 4) → (X 5)) Λ (X 3 ) ((X 3) → (X 6)) ν (¬(X 1) 2 2) 3 3) 4 4) 5 " width="640"
3) → (X 4)) Для какого из указанных значений X ложно высказывание: ((X 4) → (X 5)) Λ (X 3 ) ((X 3) → (X 6)) ν (¬(X 1) 2 2) 3 3) 4 4) 5 " width="640"
Решение задач
Для какого из указанных значений X истинны высказывания:
¬ (( X 3) → (X 4))
Для какого из указанных значений X ложно высказывание:
((X 4) → (X 5)) Λ (X 3 )
((X 3) → (X 6)) ν (¬(X
1) 2 2) 3 3) 4 4) 5

Решение задач
Для какого слова истинны высказывания:
¬ ( Первая буква слова согласная → ( вторая буква слова гласная ν последняя буква слова гласная ))
1) Горе 2) Привал 3) Кресло 4) Закон
( Первая буква слова гласная ν Пятая буква слова согласная ) → Вторая буква слова гласная
1) Арбуз 2) Ответ 3) Кресло 4) Привет

Решение задач

Решение задач
D

Решение задач

Решение задач

Решение задач

Решение задач
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z . Дан фрагмент таблицы истинности выражения F :
X
Y
1
1
Z
1
1
F
0
0
1
1
1
0
1
1
1) X ^ Y ^ ¬Z 2) X ν ¬Y ν Z
3) ¬X ν Y ν ¬Z 4 ) ¬X ν ¬Y ν ¬Z

Решение задач

Решение задач

Решение задач

Решение задач

Решение задач
Каково наибольшее целое число X , при котором истинно высказывание:
(10 (X+1)·(X+1)·(X+1))
(10 (X+1)·(X+2))
(10 (X+1)·(X+2))
(10 (X+1)·(X+1) - X)

Решение задач
Укажите значения логических переменных K, L, M, N при которых логическое выражение ложно:
(K ν M) → (M ν ¬L ν N) = 0
Укажите значения логических переменных X, Y, Z при которых логическое выражение истинно:
(X ν Y) Λ ( ¬ X) Λ ( ¬ Z Λ Y ν Z) Λ (X ν Z) = 1

Решение задач
Сколько различных решений имеет уравнение:
(¬K ν N) → (L ^ M ν K) = 0
((K ^ L) → M) ^ (N ^ K ν L) = 1
¬((L ν M) → (K ^ L ν N)) = 1

Решение задач
АНАЛИЗ СИСТЕМЫ ЛОГИЧЕСКИХ УРАВНЕНИЙ
Определить, сколько различных решений имеет система уравнений:
Нужно указать именно количество решений системы уравнения, а не записывать сами эти решения.

Решение задач
Решение
Анализируем отдельные уравнения, входящие в систему.
1
Операция «тождество»:
обе переменные – x 1 и x 5 – должны быть равны друг другу

Решение задач
Анализируем остальные уравнения.
Операция «ИЛИ»: достаточно, чтобы был равен 1 хотя бы один операнд.
x 1 = 0, x 2 = 0 или x 1 = 1, x 2 = 1
x 2 = 1, x 3 = 1
x 2 = 0, x 3 = 0

Решение задач
Возможные комбинации значений переменных ( x 1 , x 2 , x 3 ):
( 0 0 0 ),
( 1 0 0 )
( 0 0 0 ),
( 0 0 1 ),
( 1 1 0 ),
( 1 1 1 )
( 0 1 1 ),
( 1 1 1 )
Если истинна третья часть уравнения, значения остальных не важны
Если истинна вторая часть уравнения, значения остальных не важны
Если истинна первая часть уравнения, значения остальных не важны
Итого – 6 различных вариантов ( x 1 , x 2 , x 3 ): ( 0 0 0 ), ( 0 0 1 ), ( 0 1 1 ), ( 1 1 0 ), ( 1 0 0 ), ( 1 1 1 ).

Решение задач
Анализируем второе уравнение.
Операция «ИЛИ»: достаточно, чтобы был равен 1 хотя бы один операнд.
x 1 = 0, x 3 = 0 или x 1 = 1, x 3 = 1
x 3 = 1, x 4 = 1
x 3 = 0, x 4 = 0

Решение задач
Возможные комбинации значений переменных ( x 1 , x 3 , x 4 ):
( 0 0 0 ),
( 1 0 0 )
( 0 0 0 ),
( 0 0 1 ),
( 1 1 0 ),
( 1 1 1 )
( 0 1 1 ),
( 1 1 1 )
Если истинна третья часть уравнения, значения остальных не важны
Если истинна вторая часть уравнения, значения остальных не важны
Если истинна первая часть уравнения, значения остальных не важны
Итого – тоже 6 различных вариантов ( x 1 , x 3 , x 4 ): ( 0 0 0 ), ( 0 0 1 ), ( 0 1 1 ), ( 1 1 0 ), ( 1 0 0 ), ( 1 1 1 ).

Решение задач
Анализируем третье уравнение.
Операция «ИЛИ»: достаточно, чтобы был равен 1 хотя бы один операнд.
x 1 = 0, x 4 = 0 или x 1 = 1, x 4 = 1
x 4 = 1, x 5 = 1
x 4 = 0, x 5 = 0

Решение задач
Возможные комбинации значений переменных ( x 1 , x 4 , x 5 ):
Все три первых уравнения – типовые. Поэтому тройки значений соответствующих переменных в них будут всегда одни и те же, сколько бы ни было таких уравнений!
( 0 0 0 ),
( 1 0 0 )
( 0 0 0 ),
( 0 0 1 ),
( 1 1 0 ),
( 1 1 1 )
( 0 1 1 ),
( 1 1 1 )
Если истинна третья часть уравнения, значения остальных не важны
Если истинна вторая часть уравнения, значения остальных не важны
Если истинна первая часть уравнения, значения остальных не важны
Итого – еще 6 различных вариантов ( x 1 , x 4 , x 5 ): ( 0 0 0 ), ( 0 0 1 ), ( 0 1 1 ), ( 1 1 0 ), ( 1 0 0 ), ( 1 1 1 ).

Решение задач
Сводим воедино результаты, полученные для каждого уравнения в отдельности.
Объединение уравнений в систему означает, что все они должны быть истинными одновременно.
=
И ( & )

Решение задач
В этих вариантах x 1 = x 4 , тогда во втором уравнении нужно оставить только варианты, в которых x 1 = x 4 , т.е. ( x 1 , x 3 , x 4 ) = ( 0 0 0 ) и ( 1 1 1 ).
Тогда в предпоследнем уравнении нужно оставить только варианты, в которых x 1 = x 5 , т.е. ( x 1 , x 4 , x 5 ) = ( 0 0 0 ) и ( 1 1 1 ).
В этих вариантах x 1 = x 3 , тогда в первом уравнении нужно оставить только варианты, в которых x 1 = x 3 , т.е. ( x 1 , x 2 , x 3 ) = ( 0 0 0 ) и ( 1 1 1 ).
В этих вариантах x 1 = x 2 .
Тогда в результате получается, что все переменные во всех уравнениях должны быть равными:
x 1 = x 2 = x 3 = x 4 = x 5
( x 1 , x 2 , x 3 , x 4 , x 5 ) = ( 0 0 0 0 0 ) или ( 1 1 1 1 1 ), т.е. возможно два решения данной системы уравнений.
Ответ:

Решение задач

Решение задач

Решение задач
Дано выражение:
¬ ( A → B) ν ¬(X → A) = B ≡ ¬(A → X)
где X = f(A,B)
найти X
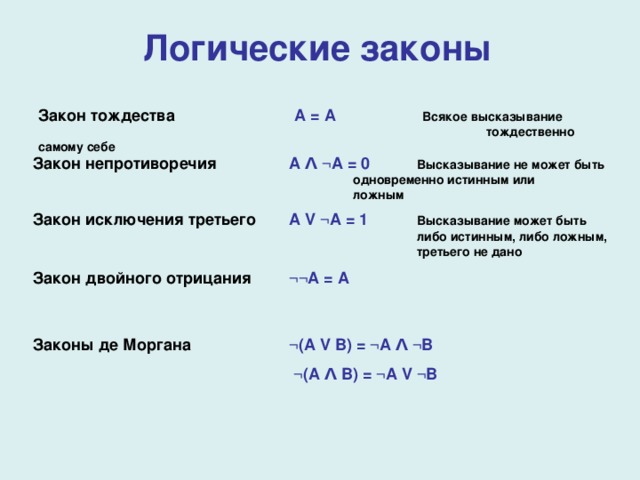
Логические законы
Закон тождества А = А Всякое высказывание тождественно самому себе
Закон непротиворечия А Λ ¬ А = 0 Высказывание не может быть одновременно истинным или ложным
Закон исключения третьего А V ¬ А = 1 Высказывание может быть либо истинным, либо ложным, третьего не дано
Закон двойного отрицания ¬¬ А = А
Законы де Моргана ¬ (А V B) = ¬ А Λ ¬B
¬ (А Λ B) = ¬ А V ¬B

Правила преобразования логических выражений
Правило коммутативности А Λ B = B Λ A
А V B = B V A
Правило ассоциативности (А Λ B ) Λ С = А Λ (B Λ C)
(А V B ) V С = А V (B V C)
Правило дистрибутивности (А Λ B ) V ( A Λ С ) = А Λ (B V C)
(А V B ) Λ ( A V С ) = А V (B Λ C)
Правило поглощения А Λ ( A V B) = A
А V A Λ B = A
Правило склеивания (А Λ B) V ( ¬A Λ B) = B
(А V B) Λ ( ¬A V B) = B

Правила преобразования логических выражений
Правила равносильности А Λ A = A
А V A = A
А V 0 = A
А V 1 = 1
А Λ 0 = 0
А Λ 1 = А
А V ¬A Λ B = A V B

Преобразование логического выражения
¬A Λ B V ¬(A V B) V A =
¬A Λ B V ¬A Λ ¬B V A =
¬A Λ (B V ¬B) V A =
¬A V A = 1
¬(A V B) Λ (A Λ ¬B) =
(A V B) Λ (¬ A V B) Λ (¬ A V ¬B) =
¬( ( A V B) → ¬(B V C)) =

Решение логического уравнения
¬ ( X V A) V ¬ ( X V ¬A) = B
¬ ( X V A) V ¬ ( X V ¬A) = ¬X Λ ¬A V ¬X Λ A = ¬X Λ (¬A V A) = ¬X
¬X = B
X = ¬B
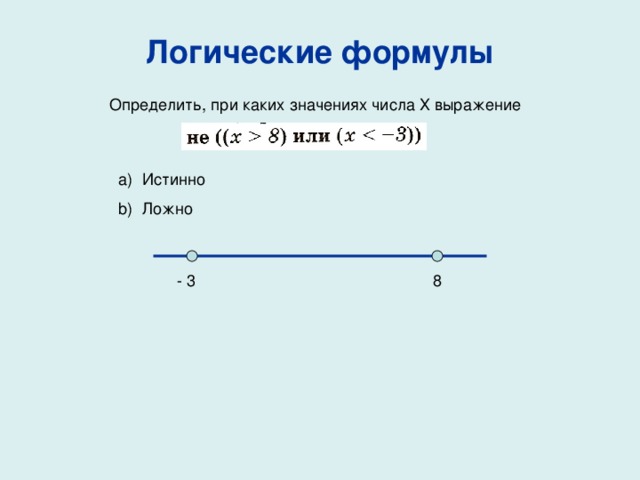
Логические формулы

Логические формулы
Y
1
X
1
-1
-1

Решение логического уравнения
(ДЗ) ¬ ( X Λ B) Λ ¬ ( X Λ ¬B) = A

Преобразование логических выражений
(ДЗ) ¬X V ¬(X V Y) V ¬(Y Λ ¬(X Λ Y) ) =

Преобразование логических выражений
(ДЗ) ¬(X V Y V ¬(X Λ Y)) Λ ¬(Y V X) =

Преобразование логических выражений
(A V B V C) Λ ¬(A V ¬B V C) =

Преобразование логических выражений
¬(B Λ C) V (A Λ C → B) =

Преобразование логических выражений
¬( ( A V B) → ¬(B V C)) =

Преобразовать логические выражения
( B C) V (¬(B A) C)
+
¬ ( A Λ B) V (A ≡ (C B))

Вычислить значение логической функции
f ( X 1, X 2, X 3) = X 1 V X 2 Λ X 3 Λ X 1 V X 3
при X 1=1, X 2=0, X 3=0
f ( X 1, X 2, X 3) = ¬X 1 V X 2 V X 3 Λ X 1 V ¬ X 3

Вычислить значение логической функции
f ( X 1, X 2, X 3) = X 1 → X 2 V X 1 → X 3
при X 1=1, X 2=0, X 3=0
f ( X 1, X 2, X 3) = X 2 → X 3 ≡ X 3 → X 1
f ( X 1, X 2, X 3) = ( X 2 → X 3) V ( X 3 → X 1)

Решить логическое уравнение
Дано выражение:
¬ ( A → B) ν ¬(X → A) = B ≡ ¬(A → X)
где X = f(A,B)
найти X

Решение логических задач
Определите, кто из учеников A, B, C и D играет, а кто не играет в шахматы, если известно следующее:
- Если А или В играет, то С не играет.
- Если В не играет, то играют С и D .
- С играет.

Решение логических задач
Определите, кто из подозреваемых участвовал в преступлении, если установлены следующие факты:
- Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал в преступлении.
- Если Иванов не участвовал, то и Сидоров не участвовал.
- Иванов не участвует в преступлении тогда, когда Сидоров в нём участвует.

Решение логических задач
Получение прибыли каких фирм означает истинность двух высказываний:
- «неверно, что фирма «В» не получит прибыль тогда, когда получат прибыль фирмы «А» или «С»;
- «получение прибыли фирмой «А» достаточно для того, чтобы получила прибыль фирма «С» , а «В» прибыль не получила»

Решение логических задач

Решение логических задач
Решение логических задач
Задачник 1 № 4 0 стр. 59

Решение логических задач

Решение логических задач

Решение задач

Решение задач

Решение задач

Решение задач

Решение задач
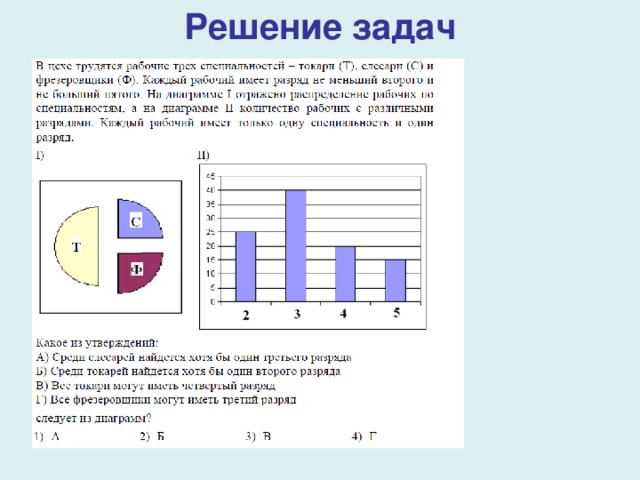
Решение задач

Решение задач
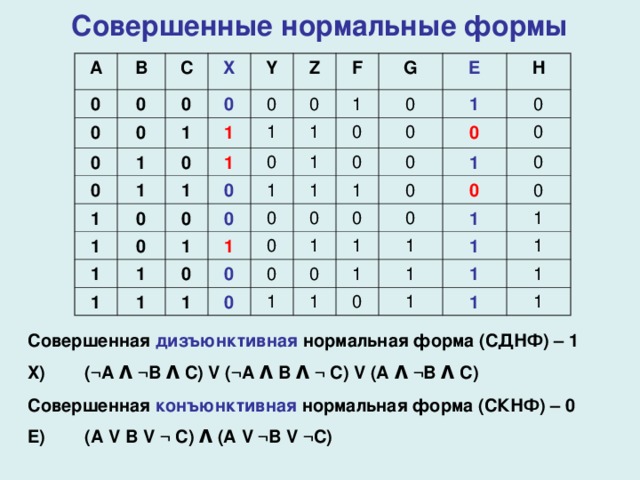
Совершенные нормальные формы
A
B
0
0
0
С
0
X
0
0
1
1
0
0
Y
Z
0
0
1
1
1
1
1
1
1
0
F
0
0
0
0
G
1
1
1
0
0
1
1
0
1
E
1
0
1
0
1
0
1
1
H
0
0
1
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
Совершенная дизъюнктивная нормальная форма (СДНФ) – 1
X) (¬A Λ ¬B Λ C) V (¬A Λ B Λ ¬ C) V (A Λ ¬B Λ C)
Совершенная конъюнктивная нормальная форма (СКНФ) – 0
E) (A V B V ¬ C) Λ (A V ¬B V ¬C)


























 3) → (X 4)) Для какого из указанных значений X ложно высказывание: ((X 4) → (X 5)) Λ (X 3 ) ((X 3) → (X 6)) ν (¬(X 1) 2 2) 3 3) 4 4) 5 " width="640"
3) → (X 4)) Для какого из указанных значений X ложно высказывание: ((X 4) → (X 5)) Λ (X 3 ) ((X 3) → (X 6)) ν (¬(X 1) 2 2) 3 3) 4 4) 5 " width="640"






































































