ЛОГИЧЕСКИЕ СОЮЗЫ «И» и «ИЛИ»
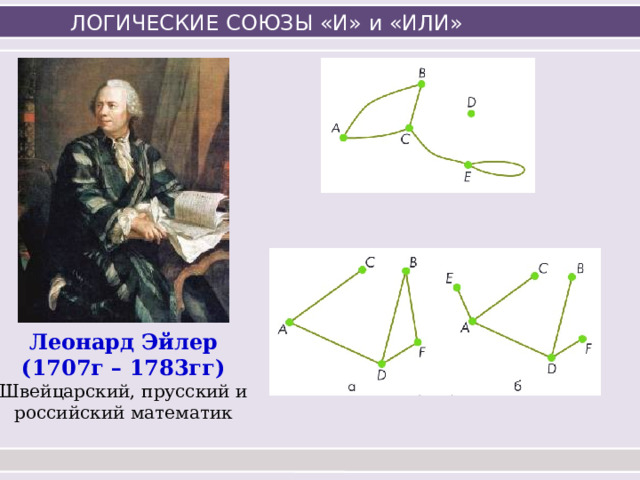
Леонард Эйлер
(1707г – 1783гг)
Швейцарский, прусский и российский математик

Повторение.
Что называется графом?
Графом называется конечное множество точек, некоторые из которых соединены линиями.
Что называется вершиной графа?
Что называется ребром графа?
Точки называются вершинами графа, а соединяющие линии – рёбрами .

Повторение.
Что называется степенью вершины?
Количество рёбер, выходящих из вершины графа, называется степенью вершины .
Свойства степеней:
В любом графе количество вершин нечётной степени чётно.
В любом графе сумма степеней вершин в два раза больше числа рёбер.
ВПР № 11 Графы.
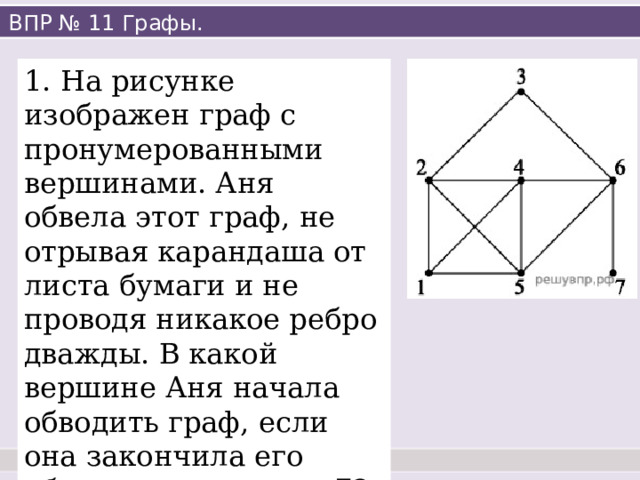
1. На рисунке изображен граф с пронумерованными вершинами. Аня обвела этот граф, не отрывая карандаша от листа бумаги и не проводя никакое ребро дважды. В какой вершине Аня начала обводить граф, если она закончила его обводить в вершине 7?
ВПР № 11 Графы.
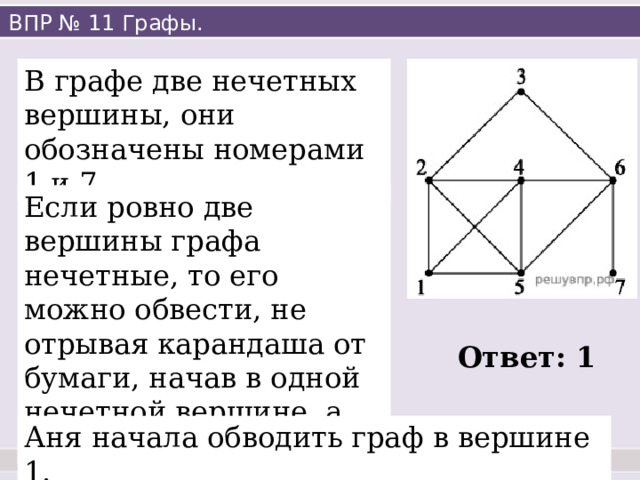
В графе две нечетных вершины, они обозначены номерами 1 и 7.
Если ровно две вершины графа нечетные, то его можно обвести, не отрывая карандаша от бумаги, начав в одной нечетной вершине, а закончив в другой
Ответ: 1
Аня начала обводить граф в вершине 1.
ВПР № 11 Графы.
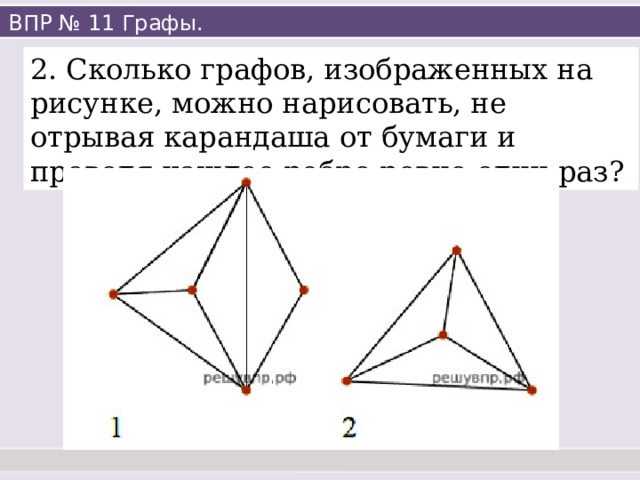
2. Сколько графов, изображенных на рисунке, можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро ровно один раз?
ВПР № 11 Графы.
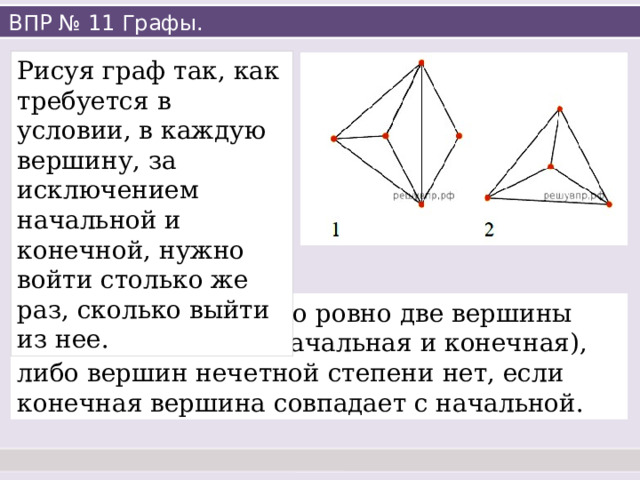
Рисуя граф так, как требуется в условии, в каждую вершину, за исключением начальной и конечной, нужно войти столько же раз, сколько выйти из нее.
Поэтому в графе либо ровно две вершины нечетной степени (начальная и конечная), либо вершин нечетной степени нет, если конечная вершина совпадает с начальной.

ВПР № 11 Графы.
2. Сколько графов, изображенных на рисунке, можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро ровно один раз?
У графа, изображенного на рисунке 1, ровно две вершины нечетной степени,
одну из них можно взять за начало, другая будет концом.
ВПР № 11 Графы.
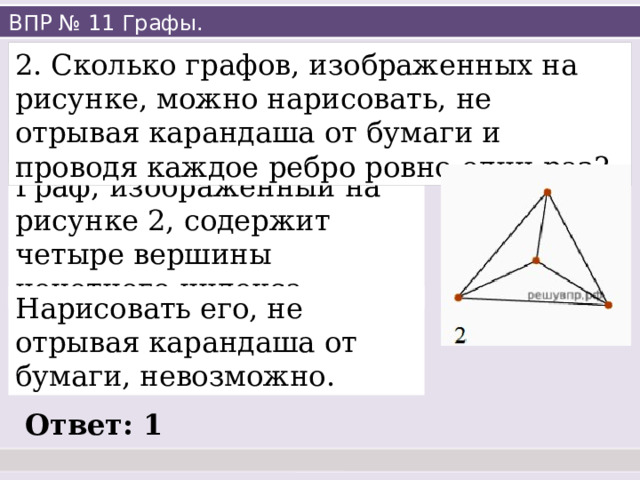
2. Сколько графов, изображенных на рисунке, можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро ровно один раз?
Граф, изображенный на рисунке 2, содержит четыре вершины нечетного индекса.
Нарисовать его, не отрывая карандаша от бумаги, невозможно.
Ответ: 1

ВПР № 11 Графы.
3. Можно ли обойти все рёбра тетраэдра, пройдя по каждому ребру ровно один раз? В ответе запишите 1, если это возможно, или 0, если невозможно.
Будем считать вершины тетраэдра вершинами графа, а ребра тетраэдра — ребрами графа.

ВПР № 11 Графы.
Обход всех ребер тетраэдра означает, что граф можно нарисовать, не отрывая каран-даша от бумаги, пройдя все ребра по одному разу.
Рисуя граф так, как требуется в условии, в каждую вершину, за исключением начальной и конечной, нужно войти столько же раз, сколько выйти из нее.

ВПР № 11 Графы.
Поэтому в графе должно быть либо ровно две вершины нечетной степени (начальная и конечная), либо вершин нечетной нет, если конечная вершина совпадает с начальной.
Но в этом графе 4 вершины нечетного индекса, поэтому требуемое невозможно.
Ответ: 0

ВПР № 11 Графы.
4. Можно ли обойти все рёбра куба, пройдя по каждому ребру ровно один раз? В ответе запишите 1, если это возможно, или 0, если невозможно.
Будем считать вершины куба вершинами графа, а ребра куба — ребрами графа.

ВПР № 11 Графы.
Обход всех ребер куба означает, что граф можно нарисовать, не отрывая карандаша от бумаги, пройдя все ребра по одному разу.
Рисуя граф так, как требуется в условии, в каждую вершину, за исключением начальной и конечной, нужно войти столько же раз, сколько выйти из нее.

ВПР № 11 Графы.
Поэтому в графе должно быть либо ровно две вершины нечетной степени (начальная и конечная),
либо вершин нечетной степени нет, если конечная вершина совпадает с начальной.
Но в этом графе 8 вершин нечетного индекса, поэтому требуемое невозможно.
Ответ: 0
ВПР № 11 Графы.
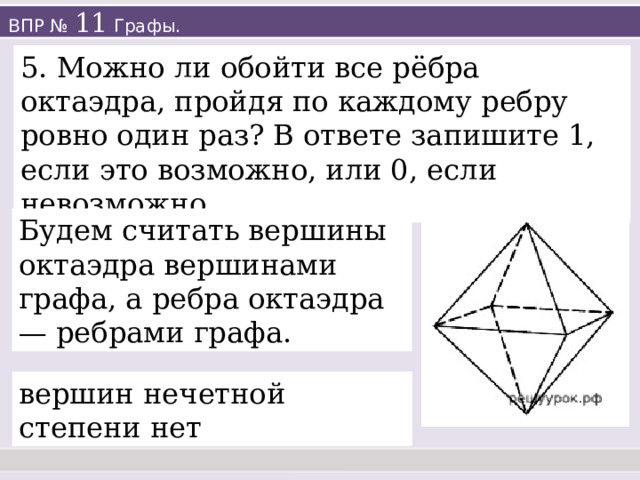
5. Можно ли обойти все рёбра октаэдра, пройдя по каждому ребру ровно один раз? В ответе запишите 1, если это возможно, или 0, если невозможно.
Будем считать вершины октаэдра вершинами графа, а ребра октаэдра — ребрами графа.
вершин нечетной степени нет
ВПР № 11 Графы.
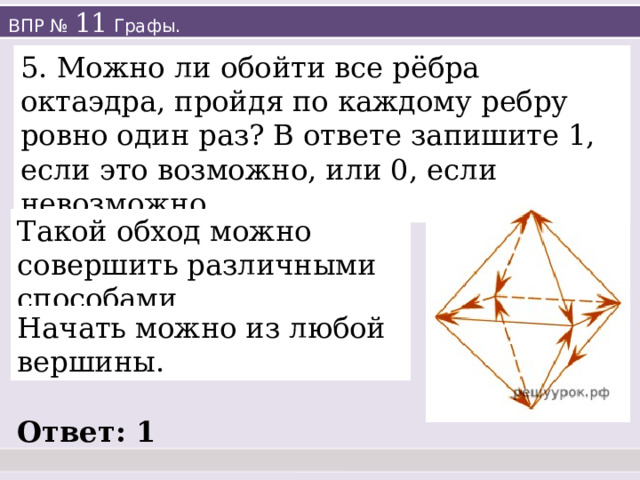
5. Можно ли обойти все рёбра октаэдра, пройдя по каждому ребру ровно один раз? В ответе запишите 1, если это возможно, или 0, если невозможно.
Такой обход можно совершить различными способами .
Начать можно из любой вершины.
Ответ: 1
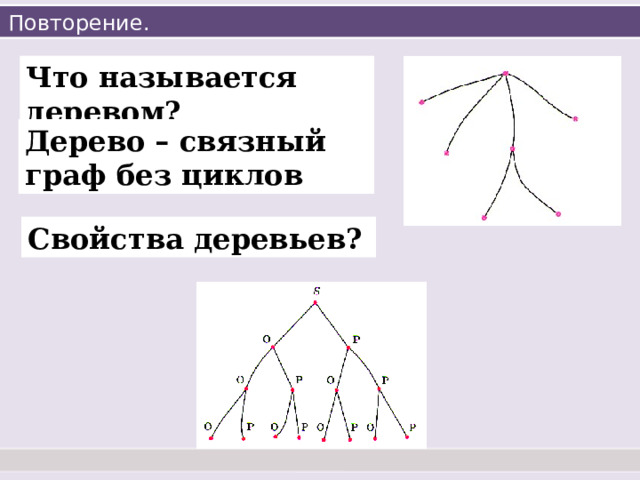
Повторение.
Что называется деревом?
Дерево – связный граф без циклов
Свойства деревьев?

Свойства деревьев:
1. Если из дерева удалить ребро, то граф перестанет быть связным.
2 . Если дерево конечно (в нем конечное число вершин) и есть хотя бы одно ребро, то в таком дереве есть концевая вершина.
3 . В конечном дереве число ребер на 1 меньше числа вершин.

Составные высказывания:
Простые высказывания нельзя разделить на более мелкие высказывания.
А: «Сейчас идёт дождь».
В: «Форточка открыта».
Составные высказывания строятся из простых высказываний с помощью логических связок
НЕ (неверно, что), И (а, но, хотя), ИЛИ.

Составные высказывания:
Составное высказывание со связкой НЕ содержит одно простое высказывание .
Составное высказывание со связкой НЕ истинно, если содержащееся в нем простое высказывание ложно.
«Число 5 является чётным» – ложное простое высказывание
«Число 5 НЕ является чётным» - истинное составное высказывание

Составные высказывания:
Составное высказывание со связкой НЕ ложно, если содержащееся в нем простое высказывание истинно.
« Последняя буква в слове «логика» является гласной» истинно.
«Последняя буква в слове «логика» НЕ является гласной» ложно.

Составные высказывания:
Работать со связкой НЕ сложно! Не всегда понятно где ее нужно поставить.
В высказывании: «Петя решил правильно все задания контрольной работы» для логической связки НЕ возможны такие предложения:

Составные высказывания:
В высказывании: «Петя решил правильно все задания контрольной работы» для логической связки НЕ возможны такие предложения:
- Петя НЕ решил правильно все задания контрольной работы.
2) Петя решил неправильно все задания контрольной работы.
3) Петя решил правильно НЕ все задания контрольной работы.
Все эти высказывания имеют разный смысл!

Составные высказывания:
По сути, с помощью логической связки НЕ мы строим отрицание исходного высказывания.
Для того что бы избежать двусмысленности при составлении высказываний со связкой НЕ, рекомендуется выбирать один из двух вариантов:

Составные высказывания:
- Использовать речевой оборот «неверно, что» и всегда ставить перед исходным высказыванием.
Пример: отрицанием высказывания «У меня дома есть компьютер» будет являться высказывание
«Неверно, что у меня дома есть компьютер»
или, что в русском языке то же самое, «У меня дома нет компьютера»

Составные высказывания:
2) Строить отрицание к сказуемому, добавляя к соответствующему глаголу частицу «не».
Пример: отрицанием высказывания «Число 324 делится на 7 ровно без остатка»
будет являться высказывание «Число 324 не делится на 7 ровно без остатка»

Составные высказывания:
Составное высказывание со связкой И содержит два простых высказывания.
Важно понимать, что составное высказывание с связкой И истинно тогда и только тогда, когда истинны оба входящие в него простые высказывания.
Пример: простые высказывания «Число 324 делится на 7», «Число 324 делится на 5» - оба ложны

Составные высказывания:
Простые высказывания «Число 324 делится на 3», «Число 324 делится на 2» - оба истинны.
Рассмотрим образованные из них с помощью логической связки И составные высказывания:
- «Число 324 делится на 7 И на 5» - ложное высказывание;
2) «Число 324 делится на 7 И на 3» - ложное высказывание;

Составные высказывания:
3) «Число 324 делится на 7 И на 2» - ложное высказывание;
4) «Число 324 делится на 5 И на 3» - ложное высказывание;
5) «Число 324 делится на 5 И на 2» - ложное высказывание;
6) «Число 324 делится на 3 И на 2» - истинное высказывание.

Составные высказывания:
Составное высказывание со связкой ИЛИ содержит два простых высказывания.
Важно понимать, что составное высказывание с связкой ИЛИ ложно тогда и только тогда, когда ложны оба входящие в него простые высказывания. Истинно тогда и только тогда когда истинны оба входящих в него простых высказывания , либо истинно одно из простых высказываний.

Составные высказывания:
Пример: составные высказывания, образованные с помощью логической связки ИЛИ
1) «Число 324 делится на 7 ИЛИ на 5» – ложное высказывание;
2) «Число 324 делится на 7 ИЛИ на 3» – истинное высказывание;
3) «Число 324 делится на 7 ИЛИ на 2» – истинное высказывание;

Составные высказывания:
Пример: составные высказывания, образованные с помощью логической связки ИЛИ
4) «Число 324 делится на 5 ИЛИ на 3» – истинное высказывание;
5) «Число 324 делится на 5 ИЛИ на 2» – истинное высказывание;
6) «Число 324 делится на 3 ИЛИ на 2» – истинное высказывание;

Составные высказывания:
Утверждение « А и ( не А)» является ложным высказыванием независимо от того, истинно или ложно утверждение А.
Утверждение « А или ( не А)» является истинным высказыванием независимо от того, истинно или ложно утверждение А.



















































