Мастер - класс по теме " Использование моделирования при обучении математике"

Мастер – класс

« Использование моделирования в обучении математике»

Цель:

Содействовать систематизации знаний учителей о моделировании и подготовке педагогов к использованию учебных моделей в образовательном процессе по математике.

Задачи:

Создать условия для организации работы по освоению педагогами учебных моделей и определению возможностей и эффективности их применения в процессе обучении математике.

1. Организационный этап.

Создание психологической готовности участников мастер-класса к совместной работе.

– Уважаемые коллеги, здравствуйте! Я рада приветствовать вас на своём мастер-классе.

Тема моего мастер-класса «Использование моделирования в обучении математике ».

Перед вами лежит таблица-фиксация знаний, заполните, пожалуйста, вторую графу «Знаю» по данной теме и отложите.

Моя цель: Способствовать систематизации знаний учителей о моделировании и подготовке педагогов к использованию учебных моделей в образовательном процессе по математике.

А Ваша цель? (ответы)

2. Актуальность.

- Как вы думаете, почему именно математика так широко представлена в программе начального образования?

Математика как учебный предмет в начальной школе призвана максимально развивать личность младшего школьника, способствовать становлению его самостоятельности в учебно-познавательной деятельности, поэтому она широко представлена в программе начального образования: 4 часа в неделю или 536 часов за курс начальной школы. Задача учителя начальной школы – сформировать у всех детей базовый уровень математических представлений и способов деятельности, необходимых для социальной адаптации в обществе. Решение этой задачи часто вызывает большие трудности, так как ни один из математических объектов в реальной действительности не существует, а мышление детей младшего школьного возраста по преимуществу наглядно-образное, способности даже к простейшему осмыслению математического материала весьма различны.

Поэтому современные требования к формированию умственных действий на уроках математики требуют применения наиболее эффективных методов и приёмов обучения. Одним из них является метод моделирования.

Метод моделирования стал одним из основных методов научного исследования. Этот метод в отличие от других является всеобщим, используется во всех науках, на всех этапах научного исследования. Он обладает огромной эвристической силой, позволяет свести изучение сложного к простому, невидимого и неощутимого – к видимому и ощутимому, незнакомого – к знакомому, т.е. сделать сложное явление реальной действительности доступным для тщательного и всестороннего изучения. В связи с этим применение моделей и моделирования в обучении, по мнению большинства ученых теоретиков, приобретает особое значение для повышения теоретического уровня педагогической науки и практики.

Необходимость овладения младшими школьниками методом моделирования как методом познания в процессе обучения можно обосновать с разных позиций.

- Как вы думаете с каких?

Во-первых, как показывают эксперименты, введение в содержание обучения понятий модели и моделирования существенно меняет отношение учащихся к учебному предмету, делает их учебную деятельность более осмысленной и более продуктивной.

Во-вторых, целенаправленное и систематическое обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивает их интеллектуальное развитие.

- В определении моделирования вставьте пропущенные слова.

«Моделирование – это метод опосредованного познания, при котором изучается не интересующий нас объект, а его заместитель (модель), находящийся в некотором объективном соответствии с познавательным объектом, способный замещать его в определённых отношениях и дающий при этом новую информацию об объекте» (Л. М. Фридман) Слайд 2

При введение моделирования в содержание обучения математике важно, чтобы учащиеся сами овладели методом моделирования, научились строить и преобразовывать модели, отражая различные отношения и закономерности, сами изучали какие-либо объекты, явления с помощью моделирования.

Когда учащиеся, решая практическую математическую задачу, понимают, что она представляет собой знаковую модель некоторой реальной ситуации, составляют последовательность различных ее моделей, затем изучают (решают) эти модели и, наконец, переводят полученное решение на язык исходной задачи, то тем самым школьники овладевают методом моделирования.

1. Знакомство с видами моделей.

- Какие виды моделей вы знаете и применяете на практике? (при затруднении предлагается выбрать из предложенных вариантов: вербальные, словесные, иллюстрационные, предметные, эвристические, схематические, математические, геометрические)

Виды моделей: вербальные, предметные, схематические, математические.

Можно выделить четыре модели, которые используются при работе над задачей на уроках математики: предметные, вербальные, схематические, математические.

Составляется кластер. (Сначала самостоятельно, а в процессе работы изменяется, пополняется, исправляются недочёты.)

Примерами предметных моделей могут быть сюжетные иллюстрации, отдельные предметы или их изображения. Слайд 3

К группе вербальных моделей мы относим в первую очередь сам текст задачи, кроме того, различные виды кратких записей текста задачи. Для некоторых текстовых задач более удобной формой вербальной модели является таблица. Слайд 4

Коля – 3

Таня - ?, на 2больше

Всего - ?

Схематические модели служат для визуального представления задачной ситуации, но здесь используются не конкретные предметы и их изображения, а различного рода условные обозначения, которые заменяют реальные предметы( например, круги, квадраты, отрезки, точки и т.п.).

Наиболее распространённые в начальной школе модели этого вида – схематические иллюстрации и схематические чертежи. Слайд 6

Под математическими моделями надо понимать математические выражения или равенства (3+4, 3+5=8). Слайд 7

Математическое выражение (например, запись вида 5+3);

Математическое равенство (например, запись вида 5+3=8).

( Раздаточный материал для групп «Виды моделей»)

4.Действия которые можно проводить с моделями.

Чтобы процесс переходов от одной модели к другой при решении текстовой задачи был продуманным, хорошо организованным и эффективным, важно разработать комплекс дидактических заданий по работе с учебными моделями.

- Давайте уточним, какие действия можно проводить с моделями?

1)Задания на соотнесение моделей: Слайд 8

при выполнении заданий на соотнесение моделей ребёнок должен определить, соответствуют ли друг другу предложенные для сравнения модели, и объяснить, почему соответствие есть или отсутствует. Например, дан рисунок, схема и равенство. Ученик рассказывает, почему схема подходит к рисунку и к равенству. Слайд 9

2) Задания на построение модели:

самостоятельно построить на парте из геометрических фигур схему, соответствующую рисунку, тексту задачи или математической записи, составить математическое выражение, соответствующее предложенному рисунку, схеме или тексту задачи. Слайд 10

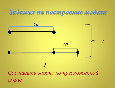
3) Задания на выбор модели:

при выполнении заданий этой группы дети из нескольких предложенных вариантов выбирают тот, который соответствует другой модели. Слайд 11

4) Примеры заданий на изменение модели:

изменить предложенную схему так, чтобы новая схема соответствовала сюжетной иллюстрации, тексту задачи, числовому выражению или равенству;

изменить предложенный текст задачи так, чтобы новый текст соответствовал сюжетной иллюстрации, схеме, числовому выражению. Слайд 12

Многие задания в учебнике можно дифференцировать.

Использование учебных моделей позволяет сделать более доступным для ребёнка восприятие и понимание текста задачи, поскольку модели помогают визуализировать скрытые при непосредственном наблюдении связи и отношения, представленные в тексте задачи.

Благодаря возможности наглядно представлять наиболее существенные характеристики изучаемого объекта, модель служит весьма продуктивным видом визуализации.

Поскольку мышление детей младшего школьного возраста по преимуществу наглядно-образное, опора на модели делает возможным приобщение учеников к некоторым (пусть самым простым) теоретическим обобщениям. Это весьма значимо на первых шагах обучения решению задачи. Однако для того, чтобы работа с моделями приводила к максимальной «отдаче», их применение должно быть последовательным и систематическим.

Слайд 13 ( пустой)

(Раздаточный материал « Группы заданий, ориентированных на выполнение одного из следующих действий :….»

5. Группы заданий, ориентированных на выполнение одного из следующих действий:

- задания на соотнесение моделей :

1. Соотнесение предметной и вербальной моделей.

2. Соотнесение предметной и схематической моделей. Подходит ли схема к рисунку?

3.Соотнесение предметной и математической моделей.

Верно ли составлен пример к рисунку?

4.Соотнесениевербальной и математической моделей.

Верно ли Ваня решил задачу?

5.Соотнесение вербальной и схематической моделей.

Проверь, верно ли Петя составил схему к задаче.

6.Соотнесение схематической и математической моделей.

Верно ли составлен пример к схеме

- выбор модели:

1. Задания на выбор модели при сравнении предметных и вербальных моделей.

Какая краткая запись подходит к рисунку?

2. Задания на выбор модели при сравнении предметных и схематических моделей.

Выбери схему к рисунку.

3. Задания на выбор модели при сравнении предметных и математических моделей.

Какой пример подходит к рисунку?

4.Задания на выбор модели при сравнении вербальных и математических моделей.

Выбери верное решение задачи.

5. Задания на выбор модели при сравнении вербальных и схематических моделей.

Выбери схему

6. Задания на выбор модели при сравнении схематических и математических моделей.

Какой пример подходит к схеме?

- изменение модели:

1. Задание на изменение модели в паре « Предметная модель – вербальная модель»

Измени рисунок так, чтобы он соответствовал тексту задачи. Или наоборот.

Измени краткую запись, чтобы она подходила к рисунку

2. Задание на изменение модели в паре « Предметная модель – схематическая модель»

Дополни схему

3. Задание на изменение модели в паре « Предметная модель – математическая модель»

Петя записал пример к рисунку. Часть примера не видна. Дополни запись.

4. Задание на изменение модели в паре « Вербальная модель – математическая модель»

Измените текст задачи, чтобы она решалась так:

5. Задание на изменение модели в паре « Вербальная модель – схематическая модель »

Исправь схему

6. . Задание на изменение модели в паре « Схематическая модель – математическая модель»

Катя сделала схему, исправь её ошибку.

- Дополни условие и вопрос, чтобы задача решалась сложением.

- Измени схему так, чтобы показать её с помощью действия вычитания

- построение модели:

1.Задание на построение модели в паре « Предметная модель – вербальная модель»

Составь задачу по рисунку или сделай рисунок к тексту задачи ( краткой записи)

2. Задание на построение модели в паре « Предметная модель – схематическая модель»

Составь схему к предложенному рисунку или, наоборот, сделай рисунок к предложенной схеме

3.Задание на построение модели в паре « Предметная модель – математическая модель»

Составь пример к рисунку

4.Задание на построение модели в паре «Вербальная модель – математическая модель»

Составь задачу, которая решается так5. Задание на построение модели в паре « Вербальная модель – схематическая модель»

Составь задачу по схеме

Составь пример по схеме или схему к выражению

6. Работа в группах:

Задания для работы в группах

1) Из предложенного ряда дидактических заданий выберите задание на соотнесение предметной и вербальной моделей при работе над задачей.

а) Верно ли составлен пример к схеме?

б) Подходит ли рисунок к задаче?

в) Проверь, верно ли Сергей решил задачу.

г) Подходит ли схема к рисунку?

д) Верно ли составлен пример к рисунку?

е) Проверь, верно ли Катя составила схему к задаче?

2) Из предложенного ряда дидактических заданий выберите задание на соотнесение предметной и вербальной моделей при работе над задачей.

а) Подходит ли схема к рисунку?

б)Проверь, верно ли Катя составила схему к задаче?

в) Проверь, верно ли Сергей решил задачу.

г) Подходит ли краткая запись к рисунку?

д) Верно ли составлен пример к рисунку?

е) Верно ли составлен пример к схеме?

3) Из предложенного ряда дидактических заданий выберите задание на соотнесение предметной и схематической моделей при работе над задачей.

а) Верно ли составлен пример к схеме?

б) Подходит ли рисунок к задаче?

в) Проверь, верно ли Сергей решил задачу.

г) Подходит ли схема к рисунку?

д) Верно ли составлен пример к рисунку?

е) Проверь, верно ли Катя составила схему к задаче?

1) Определите задание на выбор модели. Слайд 14

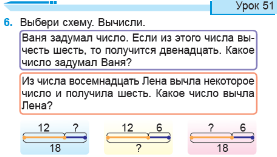
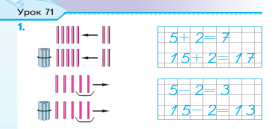
1. Определите задание на соотнесение моделей. Слайд 15

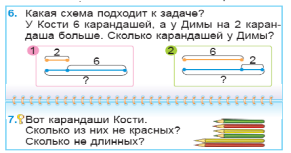
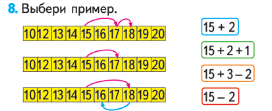
3)Определите задание на построение моделей. Слайд 16

7.Методические варианты использования моделей. Слайд 17

Методические варианты использования моделей: репродуктивно-наглядный, продуктивно-наглядный, репродуктивно-практический, продуктивно-практический. Рассмотрим примеры использование моделей для поиска решения текстовой задачи: « У Коли 3 яблока, а у Лены 2 яблока. Сколько яблок у детей вместе?»

Вариант 1. Репродуктивно-наглядный

Учитель демонстрирует модель (на доске, наборном полотне) и на её основе даёт словесное объяснение о способе решения задачи. При этом объяснение выступает репродуктивной передачей информации от учителя к детям.

Пример объяснения решения задачи:

- Ребята, я располагаю на наборном полотне 3 кружка слева, потому что у нас в задаче сказано, что у Коли было 3 яблока, и 2 кружка справа - столько яблок, по условию задачи у Лены. В задаче нужно узнать, сколько всего яблок у детей, поэтому я придвину кружки друг к другу. Значит, эта задача решается с помощью действия сложения. Давайте запишем вместе решение задачи: 3+2=5.

Вариант 2. Продуктивно-наглядный

Учитель демонстрирует модель ( на доске, на наборном полотне) и в процессе её построения проводит с детьми беседу эвристического характера с тем, чтобы дети сами «открыли» способ решения задачи. Здесь используется продуктивная форма получения знания.

Пример объяснения решения задачи:

-Дети, сейчас я покажу слева яблоки Коли, а справа яблоки Лены. Сколько кружков я должна поставить слева? Почему? (После ответов детей учитель располагает на наборном полотне 3 кружка слева.) Сколько кружков нужно расположить на наборном полотне справа? Почему? (После ответов детей учитель располагает на наборном полотне 2 кружка справа.) Что нужно сделать, чтобы показать, что мы собираем вместе яблоки Коли и Лены? ( После ответов детей учитель придвигает одни кружки к другим). Каким действием решается задача? Почему? Как запишем решение задачи?

Вариант 3. Репродуктивно-практический

Учитель строит модель ( на доске, на наборном полотне) и одновременно просит детей построить такую же модель на парте или в тетради. В ходе построения модели учитель даёт словесное объяснение репродуктивного характера о способе решения задачи.

Пример объяснения решения задачи:

-Дети, сейчас я на наборном полотне поставлю 3 кружка слева, потому что, по условию задачи, у Коли было 3 яблока, а 2 кружка справа – столько яблок у Лены. Положите вместе со мной 3 кружка на парте слева, а 2 кружка на парте справа. В задаче нужно узнать, сколько всего яблок у детей. Поэтому я придвину кружки друг к другу и вы тоже на партах придвиньте свои кружки друг к другу. Так как мы с вами придвигаем кружки, задача решается сложением. Давайте запишем вместе решение задачи: 3+2=5.

Вариант 4. Продуктивно - практический

Учитель строит модель (на доске, наборном полотне) и одновременно просит детей построить такую же модель на парте или в тетради. В процессе построения модели учитель проводит с детьми беседу эвристического характера с тем, чтобы дети сами «открыли» способ решения задачи.

Пример объяснения решения задачи

- Дети, давайте покажем слева яблоки Коли, а справа яблоки Лены. Сколько кружков мы должны показать слева? Почему? Давайте вместе сделаем это: я поставлю кружки слева на наборном полотне, а вы положите их слева у себя на парте.

Сколько кружков мы должны показать справа? Почему? Давайте вместе сделаем это: я поставлю кружки справа на наборном полотне, а вы положите их справа у себя на парте. Что нужно сделать, чтобы показать, что мы собираем вместе яблоки Коли и Лены? Правильно, нужно придвинуть кружки друг к другу. Давайте вместе сделаем это: я на наборном полотне, а вы у себя на партах. Что мы сделали, чтобы найти ответ к задаче? Значит, каким действием решается задача? Как запишем решение задачи?

При объяснении трудного для детей материала рекомендуется чаще использовать продуктивно – практический вариант моделирования, поскольку при этом обеспечивается эвристическая форма передачи информации («субъективное открытие знания») и практическая деятельность ребёнка по построению и преобразованию моделей, что особенно важно для ребёнка со средними или слабыми математическими способностями.

8. Конструкции текста задачи: Слайд 18

(Раздаточный материал для учителей )

• Условие выражено в повествовательной форме, за ним следует вопрос, выраженный вопросительным предложением; наиболее часто встречающаяся конструкция текста.

• Условие выражено в повествовательной форме, за ним следует вопрос, выраженный повествовательным предложением.

• Часть условия выражена в повествовательной форме в начале текста, затем вопросительное предложение, включающее вопрос и часть условия.

• Часть условия выражена в повествовательной форме, затем следует также повествовательное предложение, включающее вопрос и часть условия.

• Текст задачи представляет одно сложное вопросительное предложение, в котором сначала стоит вопрос задачи, затем условие.

9. Задания для работы в группах:

1 . Каждой группе подобрать из учебника или составить задачу 2,3,4,5 конструкций.

2. Практикум « Виды работ над задачей»

1) на нахождение остатка (опорное слово: осталось)

• составить задачу

• 4 вида моделей

• из групп заданий выбрать 1(блок « Задания на изменение модели»)

• изменить конструкцию задачи

2)на нахождение суммы (опорное слово: стало)

• составить задачу

• 4 вида моделей

• из групп заданий выбрать 2 (блок « Задания на соотнесение модели»)

• изменить конструкцию задачи

3)на нахождение разности (опорное слово: на сколько)

• составить задачу

• 4 вида моделей

• из групп заданий выбрать 1 (блок « Задания на построение модели»)

• изменить конструкцию задачи

10. Практикум «Разработка вспомогательных моделей, которые используются при решении задач в начальной школе» Объединение моделей в систему .

1 тип схем

?

a b

c

2 тип схем

?, на б/м

a b

с

3 тип схем

Было –

+ --

Стало --

a b

c

4 тип схем

Было –

_ --

Осталось --

a

b c

5 тип схем

_ на ?

a c

b

Рефлексия мастер-класса

- Возьмите карточку с таблицей-фиксацией, если есть, чем дополнить, впишите в третий столбик. Кто может зачитать данные своей таблицы? (Ответы участников)

- Метод « Чемодан, Корзина, Мясорубка»

17