| № Гл | Тема (Название) | Формулировка |
| 7 класс |
| 1 | Начальные геометрические сведения |
|
| Точка, прямая, отрезок, луч, угол | Т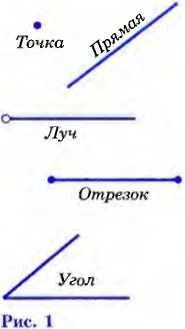  очка – это очка – это Прямая -–это линия, которая не имеет начала и конца. Луч – это прямая, которая имеет начало, но не имеет конца. Отрезок – прямая, ограниченная двумя точками. Угол – это геометрическая фигура, которая состоит из точки и двух выходящих из нее лучей. 
|
|
| Смежные углы и их свойство | Д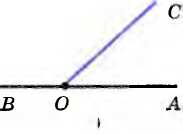 ва угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными ва угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными Свойство: сумма смежных углов равна 180°. Так как лучи ОА и ОВ образуют развернутый угол, то AOС+BOC= АОВ = 180°.
|
|
| Вертикальные углы и их свойство | Д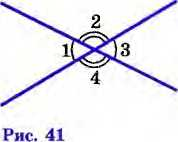 ва угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого ва угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого Свойство: вертикальные углы равны.
Угол 2 является смежным как с углом 1, так и с углом 3. По свойству смежных углов l+2 = 180° и 3+2 = 180°. Отсюда получаем: l = 180°-2, 3 = 180°-2. Таким образом, градусные меры углов 1 и 3 равны. Отсюда следует, что и сами углы равны. |
|
| Перпендикулярные прямые | Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
|
|
| Теорема о двух прямых перпендикулярных третей | Д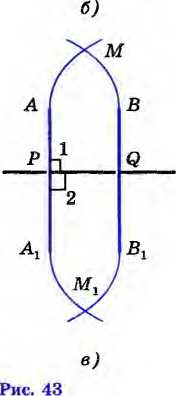 ве прямые, перпендикулярные к третьей, не пересекаются ве прямые, перпендикулярные к третьей, не пересекаются Доказательство: В самом деле, рассмотрим прямые АА1 и ВВ1 перпендикулярные к прямой PQ. Мысленно перегнем рисунок по прямой PQ так, чтобы верхняя часть рисунка наложилась на нижнюю. Так как прямые углы 1 и 2 равны, то луч РА наложится на луч PA1 Аналогично, луч QB наложится на луч QB1 Поэтому, если предположить, что прямые АА1 и ВВ1 пересекаются в точке М, то эта точка наложится на некоторую точку также лежащую на этих прямых, и мы получим, что через точки М и М1 проходят две прямые: АА1 и BB1. Но это невозможно. Следовательно, наше предположение неверно и, значит, прямые АА1 и ВВ1 не пересекаются. |
|
| Задача 70 | Ч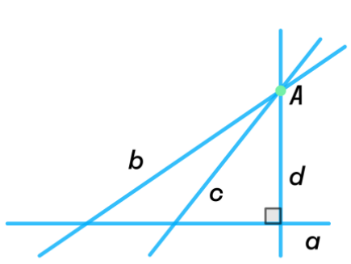 ерез точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а. ерез точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а. Дано: прямая а; 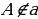 ; ; 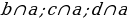 Доказать: Доказательство: Предположим, что все прямые перпендикулярны к прямой а: ba; ca; da. прямые b, c, d – не пересекаются (Две прямые, перпендикулярные к третьей, не пересекаются). Это противоречит условию наше предположение не верно. Следовательно, только одна из прямых может быть перпендикулярна прямой а, а остальные будут наклонными. |
|
| Задача 77 | Отрезок длиной m разделён: а) на три равные части; б) на пять равных частей. Н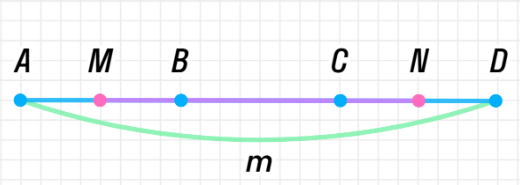 айдите расстояние между серединами крайних частей. айдите расстояние между серединами крайних частей. Решение: а) Построим отрезок AD=m. Разделим его на 3 части, поставим точки В и С: 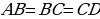
Длина каждого отрезка: 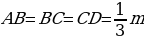 Построим точки M и N: 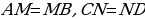 Найдем длину отрезка MN: 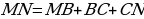 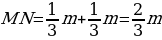
б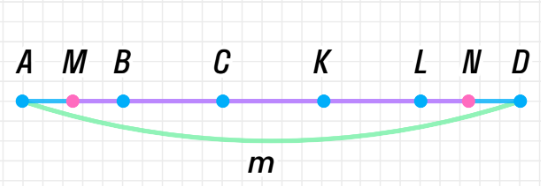 ) Построим отрезок AD=m. ) Построим отрезок AD=m. Разделим его на 5 частей, поставим точки M, В, С, K, L: 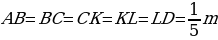
MN – отрезок между серединами крайних отрезков. 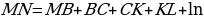
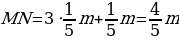
|
|
| Задача 84 | Докажите, что биссектрисы вертикальных углов лежат на одной прямой Д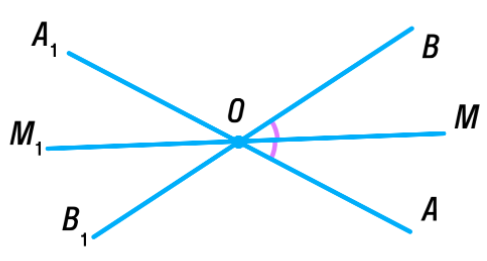 ано: ано: 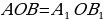 – вертикальные углы. – вертикальные углы. OM, OM1 – биссектрисы; Доказать: ММ1 – одна прямая. Доказательство: 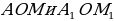 – вертикальные углы они равны. – вертикальные углы они равны.
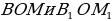 – вертикальные углы они равны. – вертикальные углы они равны.
Следовательно, 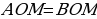 и и 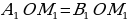 (т.к. OM, OM1 – биссектрисы) (т.к. OM, OM1 – биссектрисы) Таким образом, биссектрисы лежат на одной прямой
|
|
| Задача 85 | Д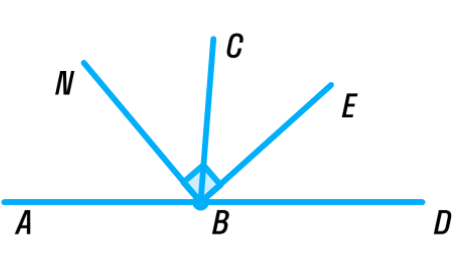 окажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой. окажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой. Дано: АВС и CBD; ВE BN – биссектрисы Доказать: точки А, В и D лежат на одной прямой Доказательство: ABD = ABС+NBC+CBE+EBD = NBC+NBC+CBE+CBE = 2NBC+2CBE = 2 (NBC + CBЕ) = 2NBE = 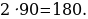 ABD - развернутый, следовательно, точки A, В и D лежат на одной прямой.
|
| 2 | Треугольники |
|
| Треугольник, виды треугольников | 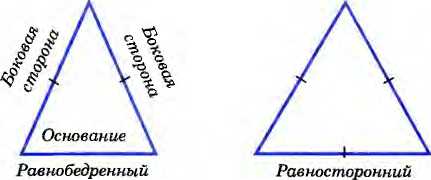 Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки называются вершинами, а отрезки — сторонами треугольника. Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки называются вершинами, а отрезки — сторонами треугольника.
Треугольники бывают: равносторонними, равнобедренными, прямоугольными, остроугольными и тупоугольными, равными. Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
|
|
| Прямоугольный треугольник и его элементы | Треугольник, в котором есть прямой угол = 900, называется прямоугольным. Два катета и гипотенуза – лежит напротив прямого угла. 
|
|
| Теорема о перпендикуляре единственности перпендикуляра, проведенного из данной точки | Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. Дано: 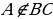 Д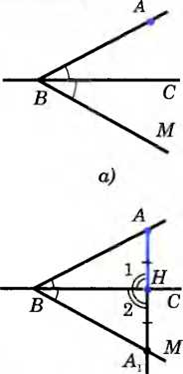 оказать: АНВС оказать: АНВС Доказательство: Отложим от луча ВС угол МВС, равный углу АВС. Так как углы АВС и МВС равны, то первый из них можно наложить на второй так, что стороны ВА и ВС первого угла совместятся со сторонами ВМ и ВС второго угла. Наглядно это наложение можно представить себе как перегибание рисунка по прямой ВС. При этом точка А наложится на некоторую точку А1 луча ВМ. 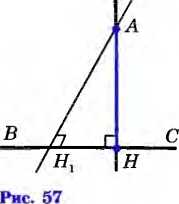 Обозначим буквой Н точку пересечения прямых АА1 и ВС. Отрезок АН и есть искомый перпендикуляр к прямой ВС. В самом деле, при указанном наложении (перегибании рисунка) луч НА совмещается с лучом НА1, поэтому 1 совмещается с 2. Следовательно, 1=2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Итак, AHBC. Обозначим буквой Н точку пересечения прямых АА1 и ВС. Отрезок АН и есть искомый перпендикуляр к прямой ВС. В самом деле, при указанном наложении (перегибании рисунка) луч НА совмещается с лучом НА1, поэтому 1 совмещается с 2. Следовательно, 1=2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Итак, AHBC.
Докажем теперь, что из точки А можно провести только один перпендикуляр к прямой ВС. Если предположить, что через точку А можно провести еще один перпендикуляр к прямой ВС, то получим, что две прямые АН и AH1 перпендикулярные к прямой ВС, пересекаются (рис. 57). Но это невозможно. Итак, из точки А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.
|
|
| Равнобедренный треугольник и его свойства | Треугольник, у которого боковые стороны равны, называется равнобедренным. Свойство: В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой Дано: △АВС – равнобедренный; AD – биссектриса. Д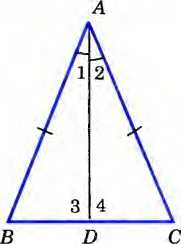 оказать: AD – медиана и высота. оказать: AD – медиана и высота. Доказательство: Из равенства треугольников ABD и ACD следует, что BD=DC и Z3=Z4. Равенство BD=DC означает, что точка D— середина стороны ВС и поэтому AD — медиана треугольника АВС. Так как углы 3 и 4 — смежные и равны друг другу, то они прямые. Следовательно, отрезок AD является также высотой треугольника АВС. Теорема доказана.
В равнобедренном треугольнике углы при основании равны. Дано: △АВС – равнобедренный; Доказать: С=В. Доказательство: Пусть AD – биссектриса. Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ=АС по условию, AD — общая сторона, 1=2, так как AD — биссектриса). В равных треугольниках против равных сторон лежат равные углы, поэтому B=C. Теорема доказана.
|
|
| Равносторонний треугольник и его свойства | Треугольник, все стороны которого равны, называется равносторонним. Распространяются свойства равнобедренного треугольника. Углы равностороннего треугольника равны (по 600). 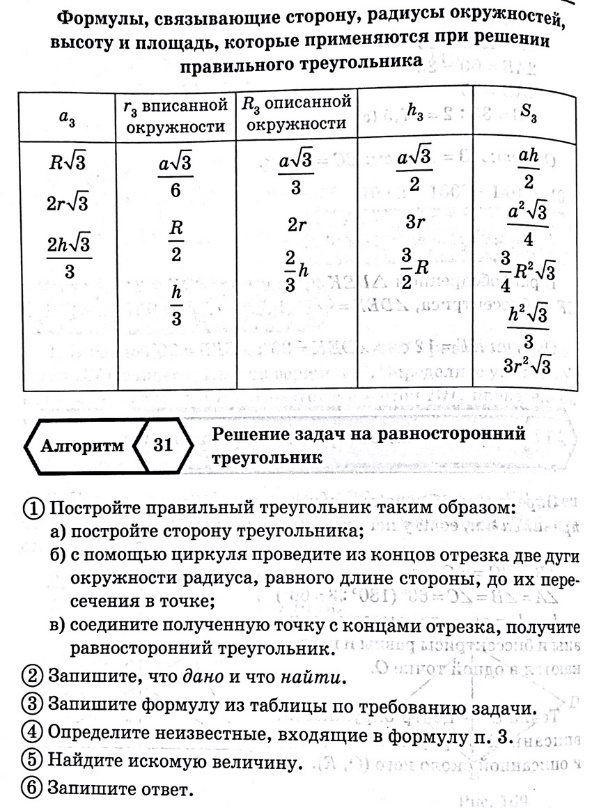 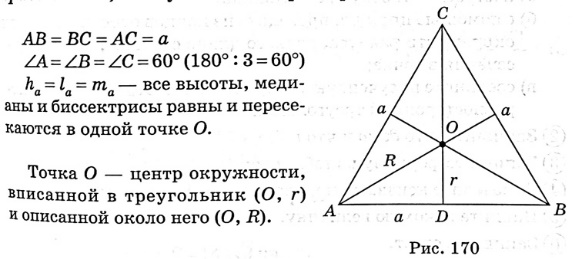
|
|
| Следствия из свойства равнобедренного треугольника | Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.  Рис. 64 Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой
|
|
| Медиана, биссектриса, высота в треугольнике | Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника Отрезок, делящий угол треугольника пополам, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке
|
|
| Первый признак равенства треугольников | Е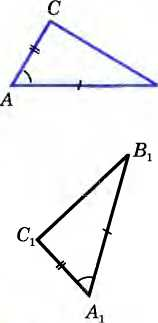 сли две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. сли две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Дано: △АВС и △А1В1С1; АВ =А1В1, АС=А1С1; А=А1 Доказать: △АВС = △А1В1С1 Доказательство: Так как A=A1 то треугольник АВС можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона АС — со стороной А1С1; в частности, совместятся точки В и B1, С и С1. Следовательно, совместятся стороны ВС и В1С1 Итак, треугольники АВС и А1В1С1 полностью совместятся, значит, они равны. Теорема доказана. |
|
| Второй признак равенства треугольников | 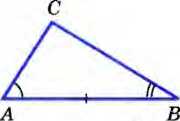 Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: △АВС и △А1В1С1; АВ =А1В1, А=А1, В=В1 Доказать: △АВС = △А1В1С1 Доказательство: 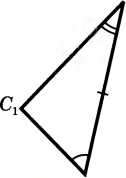 Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А совместилась с вершиной А1 сторона АВ — с равной ей стороной A1 B1, а вершины С и С1 оказались по одну сторону от прямой А1В1. Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А совместилась с вершиной А1 сторона АВ — с равной ей стороной A1 B1, а вершины С и С1 оказались по одну сторону от прямой А1В1.    Bi Аг Рис. 68 Так как A = A1 и B = B1 то сторона АС наложится на луч А1С1 а сторона ВС — на луч В1С1 Поэтому вершина С — общая точка сторон АС и ВС — окажется лежащей как на луче А1С1 так и на луче В1С1 и, следовательно, совместится с общей точкой этих лучей — вершиной С1 Значит, совместятся стороны АС и А1С1 ВС и В1С1. Итак, треугольники АВС и А1В1С1 полностью совместятся, поэтому они равны. Теорема доказана.
|
|
| Третий признак равенства треугольников | Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны Дано: △АВС и △А1В1С1; АВ=А1В1, ВС=В1С1, СА=С1А1 Доказать: △АВС = △А1В1С1 Доказательство: П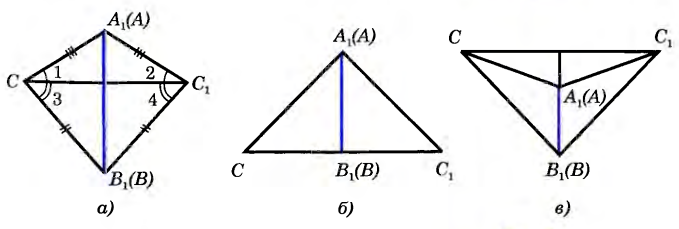 риложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершина А совместилась с вершиной А1 вершина В — с вершиной В1 а вершины С и С1 оказались по разные стороны от прямой А1В1 (рис). риложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершина А совместилась с вершиной А1 вершина В — с вершиной В1 а вершины С и С1 оказались по разные стороны от прямой А1В1 (рис). Возможны три случая: луч С1С проходит внутри угла А1С1В1 (рис. а); луч С1С совпадает с одной из сторон этого угла (рис. б); луч C1C проходит вне угла А1С1В1 (рис. в). Рассмотрим первый случай (остальные случаи рассмотрите самостоятельно). Так как по условию теоремы стороны АС и A1C1, ВС и В1С1 равны, то треугольники А1С1С и В1С1С — равнобедренные (см. рис. а). По теореме о свойстве углов равнобедренного треугольника 1 =2, 3 = 4, поэтому А1СВ1 =А1С1В1. Итак, 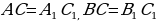 C=C1. C=C1. Следовательно, треугольники АВС и А1В1С1 равны по первому признаку равенства треугольников. Теорема доказана.
|
|
| Окружность, центр окружности, радиус, диаметр, хорда, дуга. | О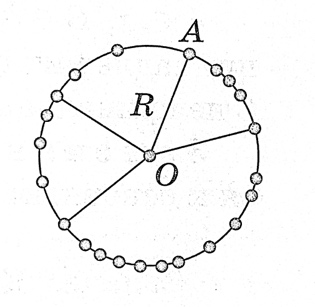 кружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. кружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности. Из определения окружности следует, что все радиусы имеют одну и ту же длину. Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется её диаметром. Диаметр равен двум радиусам. Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Часть плоскости, ограниченная окружностью, называется кругом
|
|
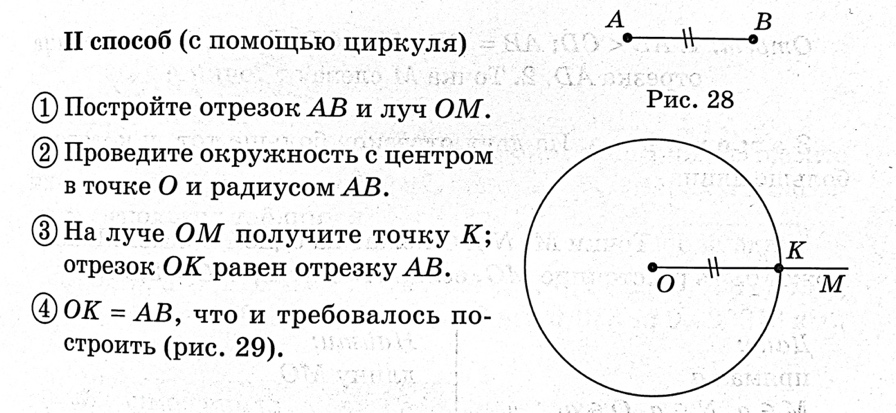
| Задачи на построение | Построить отрезок, равный данному
Построить угол, равный данному 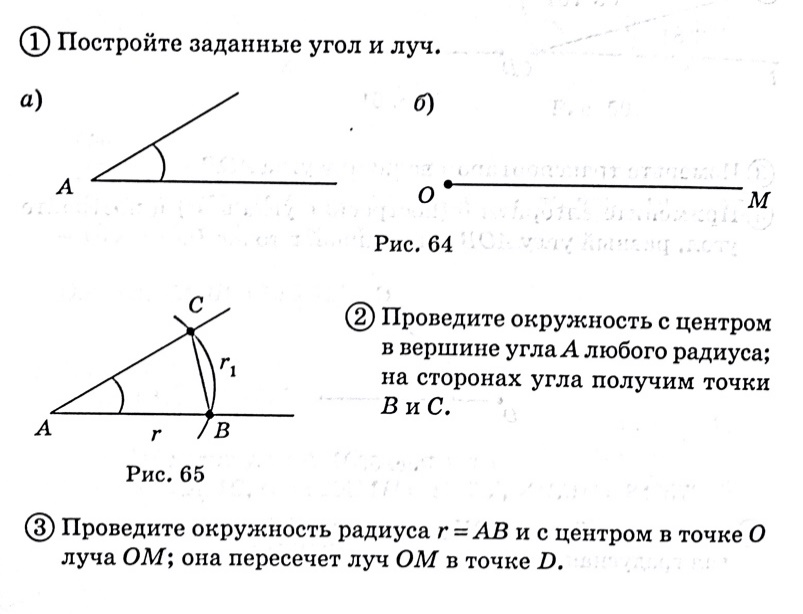
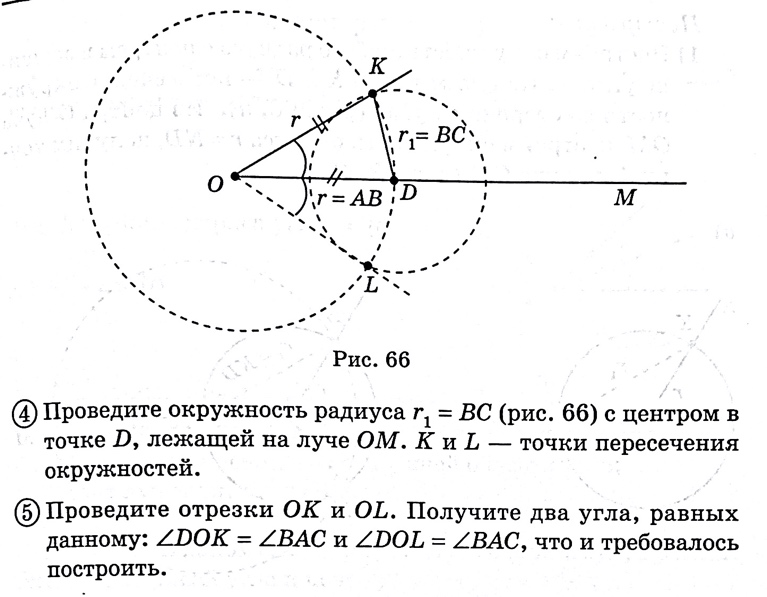
Построить биссектрису угла 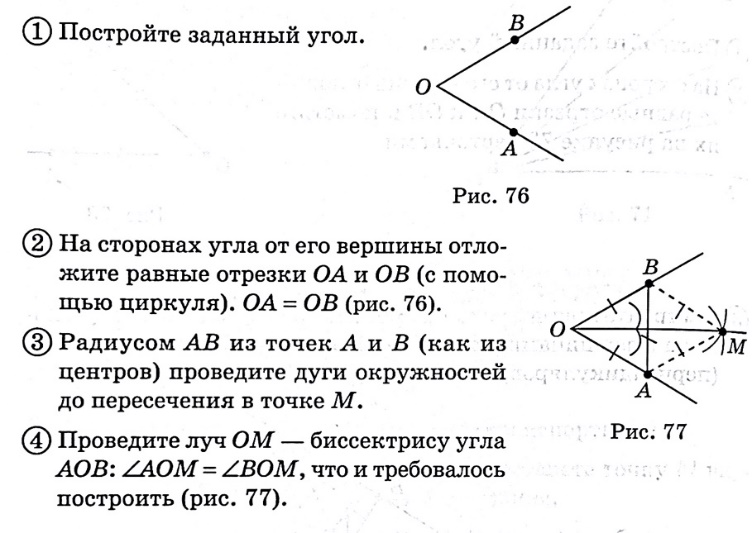
Построить середину отрезка 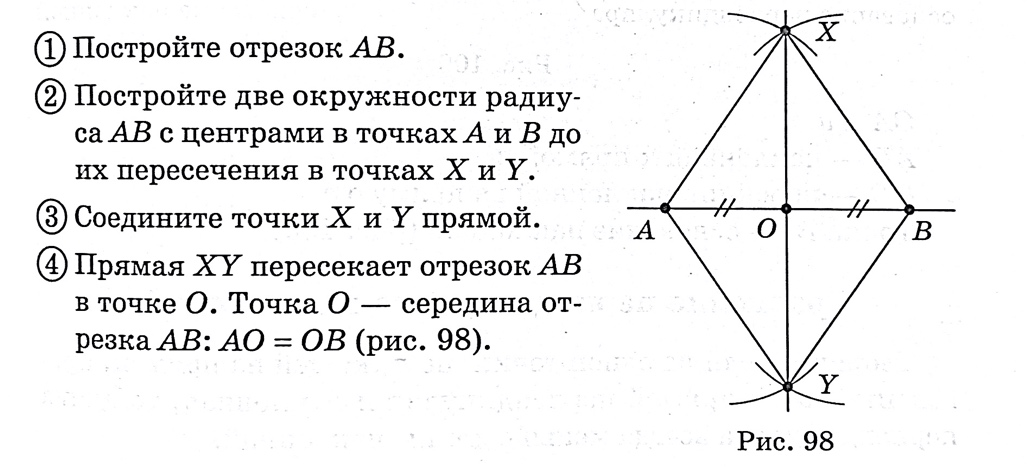
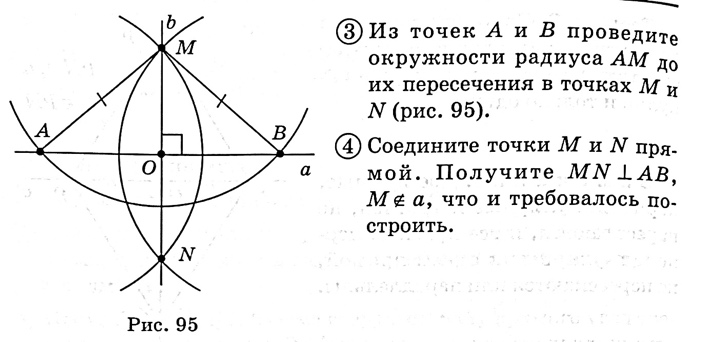
П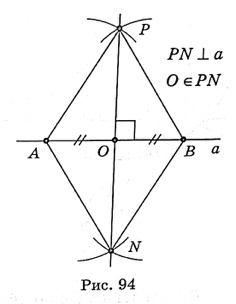 остроить перпендикуляр к прямой остроить перпендикуляр к прямой 
|
|
| Задача 159 | Докажите, что два равнобедренных треугольника равны, если боковая сторона и угол, противолежащий основанию, одного треугольника соответственно равны боковой стороне и углу, противолежащему основанию, другого треугольника. Д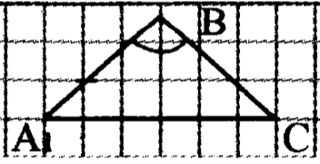 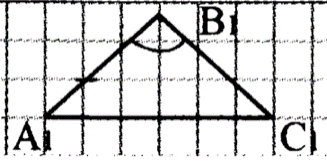 ано: АВС и А1В1С1; ано: АВС и А1В1С1; 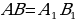 ; ; 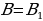 Доказать: АВС = А1В1С1 Доказательство: Так как АВС и А1В1С1 - равнобедренные, то АВ = ВС, 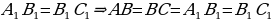 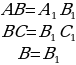 АВС = А1В1С1 (по2 сторонам и угла между ними). АВС = А1В1С1 (по2 сторонам и угла между ними).
|
|
| Задача 163 | Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника Д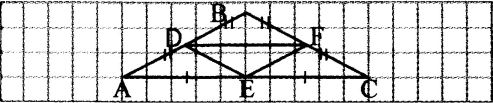 ано: АВС – равнобедренный ано: АВС – равнобедренный AD = DB; BF = FC; АE = СЕ Доказать: DFE – равнобедренный Доказательство: AD = FС (по условию), АE = СЕ (по условию), А = С (так как АВС – равнобедренный) = ADЕ = СFE (по 2 сторонам и угла между ними) = DE = EF = DFE – равнобедренный.
|
|
| Задача 173 | Докажите, что угол, смежный с углом треугольника, больше каждого из двух других углов треугольника. Д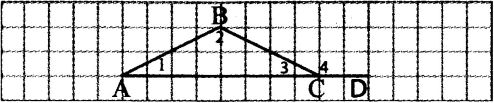 ано: ано: Доказать: Доказательство: Сумма углов треугольника равна 180°, то есть l + 2 + 3 = 180°.
3 и 4 - смежные, значит 3 + 4 = 180°. Приравняем оба равенства, 1 + 2 + 3 = 3 + 4; l + 2 = 4, так как в треугольнике все углы больше 0°, то 42 и 41.
|
|
| Задача 180 | П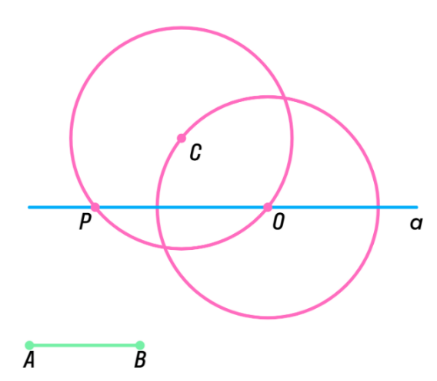 остройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой. остройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой. Дано: точка С и отрезок АВ Построение: Построим окружность с центром в точке С и радиусом АВ; Эта окружность пересечет прямую а в двух точках, в одной точке или не пересечет; В зависимости от этого задача будет иметь два решения, одно решение или не иметь решений. (на рисунке показан пример с пересечением прямой и окружности в 2-х точках) |
|
| Задача 181 | П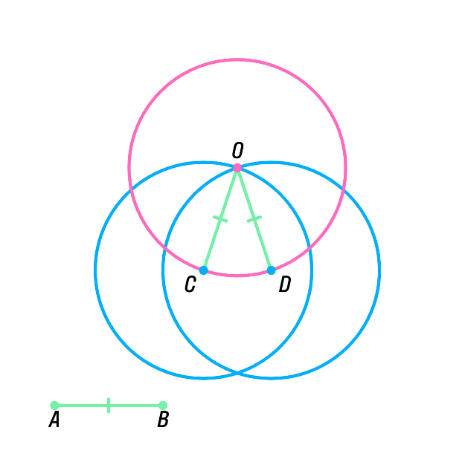 остройте окружность данного радиуса, проходящую через две данные точки. остройте окружность данного радиуса, проходящую через две данные точки.
Дано: AB – радиус окружности; C и D – точки. Построение: Построить окружности радиусом АВ с центром в точках C и D. Обозначить точку пересечения окружностей – О. Построим окружность радиусом OD. Это и будет искомая окружность. |
|
| Задача 184 | Н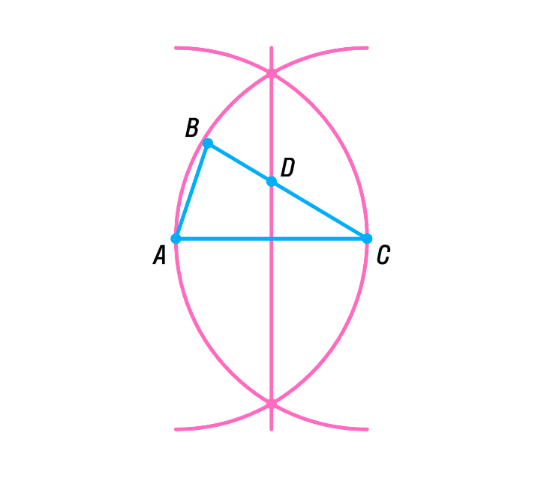 а стороне BC треугольника ABC Постройте точку, равноудалённую от вершин A и C. а стороне BC треугольника ABC Постройте точку, равноудалённую от вершин A и C. Дано: Построение: Построим две окружности с центром в точке А и С и одинаковыми радиусами AC; Эти окружности пересекаются в точках E и N. EN и ВС пересекаются в точке D – нужная точка. Доказательство: Рассмотрим △ACD, DO - серединный перпендикуляр = △ACD - равнобедренный = AD = АС. |
|
| Задача 185 | С помощью циркуля и линейки разделите данный отрезок на 4 равные части. Дано: Построение: Чтобы разделить отрезок на 4 равные части, надо разделить его пополам. Затем, каждую половину – еще раз пополам.
|
| 3 | Параллельные прямые |
|
| Параллельные прямые и отрезки | Две прямые на плоскости называются параллельными, если они не пересекаются. Два отрезка называются параллельными, если они лежат на параллельных прямых. |
|
| Секущая; углы, которые образуются при пересечении двух параллельных прямых секущей (определения) | П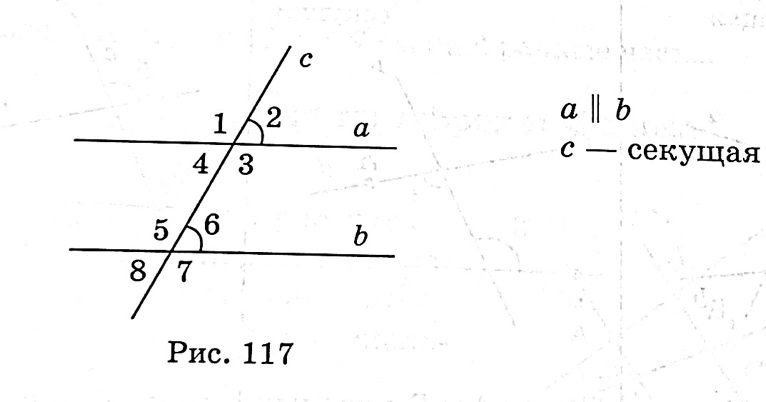 рямая с называется секущей по отношению к прямым а и в, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия: рямая с называется секущей по отношению к прямым а и в, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия: накрест лежащие углы: 3 и 5, 4 и 6; односторонние углы: 4 и 5, 3 и 6; соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
|
|
| Первый признак параллельности прямых | Е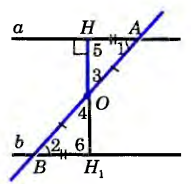 сли при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. сли при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Дано: a,bc; 1=2 Доказать: a||b Доказательство: Докажем, что а\\Ь. Если углы 1 и 2 прямые, то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны. Рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой а. На прямой b от точки В отложим отрезок ВН1 равный отрезку АН, как показано на рисунке, и проведем отрезок OH1 Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО = ВО, АН =BH1 1=2), поэтому 3=4 и 5= 6. Из равенства 3=4 следует, что точка Н1 лежит на продолжении луча ОН, т. е. точки Н, О и Н1 лежат на одной прямой, а из равенства 5=6 следует, что угол 6— прямой (так как угол 5 — прямой). Итак, прямые а и b перпендикулярны к прямой НН1 поэтому они параллельны. Теорема доказана. |
|
| Второй признак параллельности прямых | Е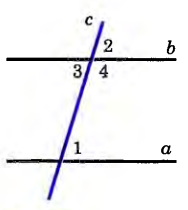 сли при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны сли при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны Дано: 1=2; a,bc Доказать: a||b Доказательство: Так как углы 2 и 3 — вертикальные, то 2=3. Из этих двух равенств следует, что 1=3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и Ь параллельны. Теорема доказана
|
|
| Третий признак параллельности прямых | Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны Дано: a,bc; 1+4=180 Доказать: a||b Доказательство: смотреть рисунок в предыдущем доказательстве! Так как углы 3 и 4 — смежные, то 3+4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.
|
|
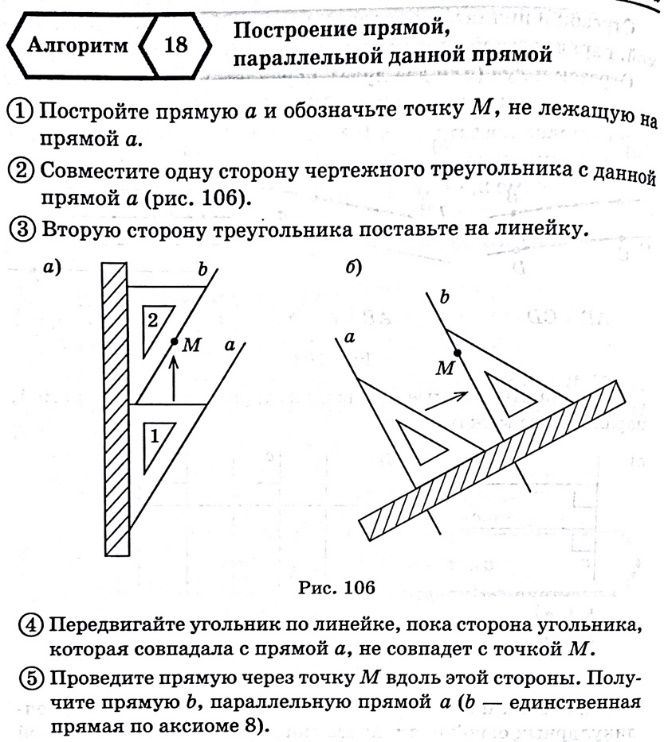
| Построение параллельных прямых |
Выбрать произвольную точку В на прямой а и построить окружность произвольного радиуса и поставить точку А. На пересечении окружности и прямой отметить точку С. Тем же радиусом АВ построить окружность с центром в точке С. Прежним радиусом АВ построить окружность с центром в точке А. Отметить точку пересечения второй и третьей окружностях D. Через точки A и D провести прямую. Полученная прямая будет параллельна данной.
Также можно построить параллельные прямые через построения перпендикулярных прямых к третьей.
|
|
| Аксиома. Аксиомы планиметрии | Аксиома – утверждение, не требующее доказательства. через любые две точки проходит прямая, и притом только одна на любом луче от его начала можно отложить отрезок, равный данному, н притом только один от любого луча в заданную сторону можно отложить угол, равный данному неразвёрнутому углу, и притом только один
|
|
| Аксиома параллельных прямых | Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
|
|
| Следствия из аксиомы параллельных прямых | Е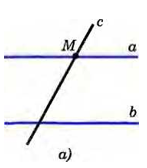 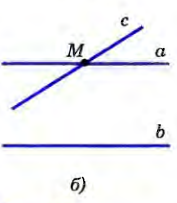 сли прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. сли прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Действительно, пусть прямые а и b параллельны и прямая с пересекает прямую а в точке М (рис. а). Докажем, что прямая с пересекает и прямую b. Если бы прямая с не пересекала прямую b, то через точку М проходили бы две прямые (прямые а и с), параллельные прямой b (рис. б). Но это противоречит аксиоме параллельных прямых, и, значит, прямая с пересекает прямую b. Если две прямые параллельны третьей прямой, то они параллельны Д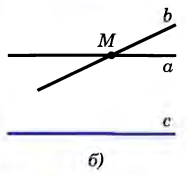 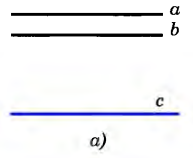 ействительно, пусть прямые а и Ь параллельны прямой с (рис. а). Докажем, что а||b. Допустим, что прямые а и b не параллельны, т. е. пересекаются в некоторой точке М (рис. б). Тогда через точку М проходят две прямые (прямые а и b), параллельные прямой с. ействительно, пусть прямые а и Ь параллельны прямой с (рис. а). Докажем, что а||b. Допустим, что прямые а и b не параллельны, т. е. пересекаются в некоторой точке М (рис. б). Тогда через точку М проходят две прямые (прямые а и b), параллельные прямой с. Но это противоречит аксиоме параллельных прямых. Поэтому наше предположение неверно, а значит, прямые а и b параллельны. |
|
| Обратная теорема | Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы |
|
| Теоремы об углах, образованных двумя параллельными прямыми и секущей | 
Следствие: если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой
|
|
| Задача 212. Углы с соответственно параллельными сторонами. | Докажите, что если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180°. Решение П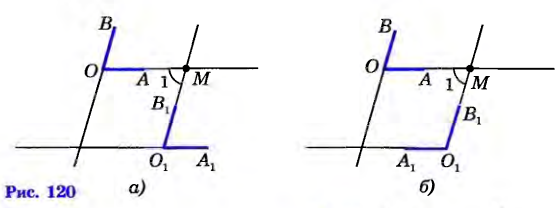 усть АОВ и А1О1В1 — данные углы и OA||O1A1, OB||O1B1. Если АОВ развернутый, то и А1О1В1 — развернутый (т.к. они лежат на параллельных прямых), поэтому эти углы равны. Пусть АОВ — неразвернутый угол. Возможные случаи расположения углов АОВ и А1О1В1 изображены на рисунке 120, а и б. Прямая О1В1 пересекает прямую и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М. Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов, образованных при пересечении прямых О1В1 и ОА (угол 1 на рисунке 120), равен углу АОВ (как накрест лежащие углы). Параллельные прямые ОА и ОА1 пересечены секущей О1М, поэтому либо 1=A1O1B1 (рис. 120, а), либо 1+ A1O1B1 = 1800 (рис. 120, б). Из равенства 1=AOB и последних двух равенств следует, что либо AOB=A1O1B1 (см. рис. 120, а), либо AOB + A1O1B1 =180° (см. рис. 120, б), что и требовалось доказать. усть АОВ и А1О1В1 — данные углы и OA||O1A1, OB||O1B1. Если АОВ развернутый, то и А1О1В1 — развернутый (т.к. они лежат на параллельных прямых), поэтому эти углы равны. Пусть АОВ — неразвернутый угол. Возможные случаи расположения углов АОВ и А1О1В1 изображены на рисунке 120, а и б. Прямая О1В1 пересекает прямую и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М. Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов, образованных при пересечении прямых О1В1 и ОА (угол 1 на рисунке 120), равен углу АОВ (как накрест лежащие углы). Параллельные прямые ОА и ОА1 пересечены секущей О1М, поэтому либо 1=A1O1B1 (рис. 120, а), либо 1+ A1O1B1 = 1800 (рис. 120, б). Из равенства 1=AOB и последних двух равенств следует, что либо AOB=A1O1B1 (см. рис. 120, а), либо AOB + A1O1B1 =180° (см. рис. 120, б), что и требовалось доказать.
|
|
| Задача 218 | Две прямые пересекаются. Можно ли провести такую прямую, которая пересекает одну прямую и параллельна другой прямой. Ответ обоснуйте Д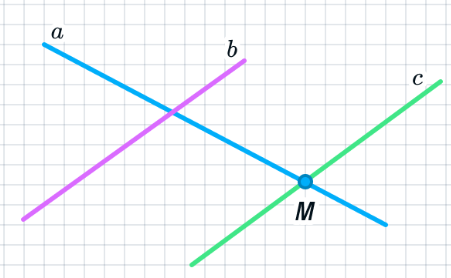 ано: ано: 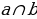 ; ; 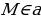 Доказать: 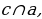 c||b c||b Доказательство: Возьмем любую точку Мb и Ма. По аксиоме параллельных прямых через точку можно построить прямую с, параллельную b, и только
одну. Так как b||c аb, то ac. Следовательно, можно построить прямую, параллельную прямой b и пересекающую прямую a.
|
|
| Задача 219 ??? | Даны две прямые а и b. Докажите, что если любая прямая, пересекающая прямую а, пересекает и вторую прямую, то данные прямые а и b параллельны. Дано: а и b – прямые, 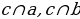 . . Доказать: а || b Доказательство: Допустим, что аb = А, тогда возможны случаи: Первый – abc =A, второй – 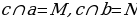 В третьем случае прямая с не переcекает прямую b, что противоречит условию b предположение, что аb неверно, а верно, что а || b ч.т.д. |
|
| Задача 220 | 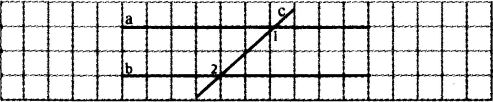 Докажите, что если при пересечении двух прямых секущей накрест лежащие углы не равны, то данные прямые пересекаются. Докажите, что если при пересечении двух прямых секущей накрест лежащие углы не равны, то данные прямые пересекаются.
Дано: 1 ≠ 2 Доказать: а b Доказательство: Если 1 и 2 – накрест лежащие углы при прямых а и b и секущей с; 1 ≠ 2 = а не параллельна b. Если прямые на плоскости не параллельны, то они пересекаются= а b. ч.т.д. |
|
| Задача 222 | Объясните, как как построить прямую проходящую через данную точку и параллельную данной прямой. (Смотри объяснение выше ) |
| 4 | Соотношение между сторонами и углами треугольника |
|
| Теорема о сумме углов в треугольнике | Сумма углов в треугольнике составляет 180° Д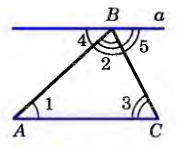 ано: АВС; ано: АВС; Доказать: A+B + C= 180° Доказательство: Проведем через вершину В прямую а, параллельную стороне АС. Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС. Поэтому 4=1, 5=3. (1) Очевидно, сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е. 4+2+5 = 180°. Отсюда, учитывая равенства (1), получаем: l+2+3 = 180°, или A+B+C= 180°. Теорема доказана.
|
|
| Внешний угол треугольника и его свойство | В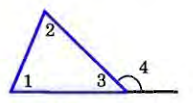 нешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. нешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Так как 4+3 = 180°, а по теореме о сумме углов треугольника (l+2) + 3 = 180°, то 4 = 1+2, что и требовалось доказать
|
|
| Теорема о соотношение между сторонами и углами треугольника | В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона Дано: АВС; 1) АВ АС; 2) CB Доказать: 1) CB. 2) АВ АС Д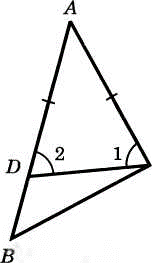 оказательство: оказательство: Отложим на стороне АВ отрезок AD, равный стороне АС. Так как АDD лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, C1. Угол 2 — внешний угол треугольника BDC, поэтому 2B. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, C1, 1=2, 2B. Отсюда следует, что C B Предположим, что это не так. Тогда либо АВ=АС, либо АВ АВС — равнобедренный и, значит, C=B. Во втором случае BC (против большей стороны лежит больший угол). И то и другое противоречит условию: CB. Поэтому наше предположение неверно, и, следовательно, АВ АС. Теорема доказана
|
|
| Следствия из теоремы (для прямоугольного и равнобедренного треугольника) | В прямоугольном треугольнике гипотенуза больше катета. В самом деле, гипотенуза лежит против прямого угла, а катет — против острого. Так как прямой угол больше острого, то гипотенуза больше катета Если два угла треугольника равны, то треугольник равнобедренный Пусть в треугольнике два угла равны. Тогда равны и стороны, лежащие против этих углов. Действительно, если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны). Итак, в треугольнике две стороны равны, т. е. треугольник — равнобедренный |
|
| Теорема о неравенстве сторон треугольника | К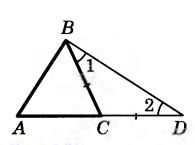 аждая сторона треугольника меньше суммы двух других сторон. аждая сторона треугольника меньше суммы двух других сторон. Дано: АВС; Доказать: АВ Доказательство: Отложим на продолжении стороны АС отрезок CD, равный стороне СВ. В равнобедренном треугольнике BCD 1=2, а в треугольнике ABD ABD 1 и, значит, ABD 2. Так как в треугольнике против большего угла лежит большая сторона, то ABAD. Но AD =AC+CD=AC+CB, поэтому АВ Теорема доказана |
|
| Следствие из теоремы | Для любых трёх точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ АС ВС |
|
| Прямоугольный треугольник и его элементы | Треугольник, в котором есть прямой угол = 900, называется прямоугольным. Два катета и гипотенуза – лежит напротив прямого угла Смотри выше |
|
| Свойства прямоугольных треугольников | Сумма двух острых углов прямоугольного треугольника равна 90 В самом деле, сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника равна 90 Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Рассмотрим прямоугольный △АВС, в котором A — прямой, B=30° и, значит, C=60°. Докажем, что 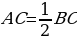 . . 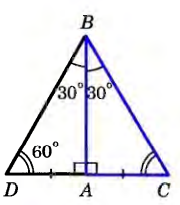 Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке. Получим треугольник BCD, в котором B=D=60°, поэтому DC=BC. Но Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке. Получим треугольник BCD, в котором B=D=60°, поэтому DC=BC. Но 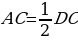 . Следовательно, . Следовательно, 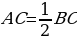 , что и требовалось доказать , что и требовалось доказать Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине гипотенузы ВС. Докажем, что ABC=30°. Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке. Получим равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу (по теореме о сумме углов в треугольнике), поэтому каждый из них равен 60°. В частности, DBC = 60°. Но DBC=2ABC. Следовательно, ABC = 30°, что и требовалось доказать.
|
|
| Признаки равенства прямоугольных треугольников | Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. Доказывается через второй признак равенства треугольников
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны Из свойства: сумма острых углов в прямоугольном треугольнике равна 90, следует, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников, т. е. по стороне (гипотенузе) и двум прилежащим к ней углам. Теорема доказана. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны Рассмотрим треугольники АВС и A1B1C1 у которых углы С и С1 — прямые, АВ=А1В1, ВС=В1С1 (рис.). Докажем, что △авс=△а1в1с1. Так как C=C1 то треугольник АВС можно наложить на треугольник А1В1С1 так, что вершина С совместится с вершиной С1, а стороны СА и СВ наложатся соответственно на лучи С1А1 и С1В1 Поскольку С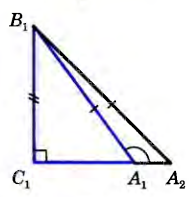 В=С1В1 то вершина В совместится с вершиной В1. Но тогда вершины А и А1 также совместятся. В самом деле, если предположить, что точка А совместится с некоторой другой точкой А2 луча А1А2, то получим равнобедренный треугольник А1В1А2 в котором углы при основании АгА2 не равны (A2 — острый, a A1 — тупой как смежный с острым углом В=С1В1 то вершина В совместится с вершиной В1. Но тогда вершины А и А1 также совместятся. В самом деле, если предположить, что точка А совместится с некоторой другой точкой А2 луча А1А2, то получим равнобедренный треугольник А1В1А2 в котором углы при основании АгА2 не равны (A2 — острый, a A1 — тупой как смежный с острым углом 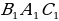 . Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А1В1С1, т. е. они равны. Теорема доказана. . Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А1В1С1, т. е. они равны. Теорема доказана.
|
|
| Расстояние от точки до прямой | П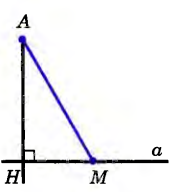 усть отрезок АН — перпендикуляр, проведенный из точки А к прямой а, М — любая точка прямой а, отличная от Н (рис.). Отрезок AM называется наклонной, проведенной из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы AM. Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой. усть отрезок АН — перпендикуляр, проведенный из точки А к прямой а, М — любая точка прямой а, отличная от Н (рис.). Отрезок AM называется наклонной, проведенной из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы AM. Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой. Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
|
|
| Свойство параллельных прямых | Все точки каждой из двух параллельных прямых равноудалены от другой прямой Р ассмотрим параллельные прямые а и b. Отметим на прямой а точку А и проведем из этой точки перпендикуляр АВ к прямой b (рис.). Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ. ассмотрим параллельные прямые а и b. Отметим на прямой а точку А и проведем из этой точки перпендикуляр АВ к прямой b (рис.). Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ. Проведем из точки X перпендикуляр XY к прямой b. Так как ХУb, то ХУа. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY — общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых а и Ь секущей AY). Следовательно, XY=AB. Итак, любая точка X прямой а находится на расстоянии АВ от прямой Ь. Очевидно, все точки прямой b находятся на таком же расстоянии от прямой а. Теорема доказана.
|
|
| Расстояние между прямыми | Из доказанной выше теоремы следует, что точка, движущаяся по одной из параллельных прямых, все время находится на одном и том же расстоянии от другой прямой. Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
|








 ва угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными
ва угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными ва угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого
ва угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого ве прямые, перпендикулярные к третьей, не пересекаются
ве прямые, перпендикулярные к третьей, не пересекаются ерез точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а.
ерез точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а.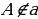 ;
; 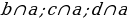
 айдите расстояние между серединами крайних частей.
айдите расстояние между серединами крайних частей.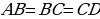
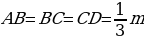
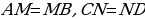
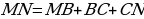
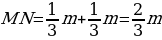
 ) Построим отрезок AD=m.
) Построим отрезок AD=m. 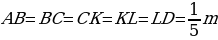
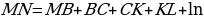
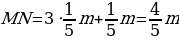
 ано:
ано: 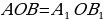 – вертикальные углы.
– вертикальные углы.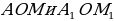 – вертикальные углы они равны.
– вертикальные углы они равны.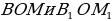 – вертикальные углы они равны.
– вертикальные углы они равны.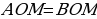 и
и 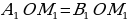 (т.к. OM, OM1 – биссектрисы)
(т.к. OM, OM1 – биссектрисы) окажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой.
окажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой.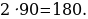
 Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки называются вершинами, а отрезки — сторонами треугольника.
Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки называются вершинами, а отрезки — сторонами треугольника.
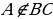
 оказать: АНВС
оказать: АНВС Обозначим буквой Н точку пересечения прямых АА1 и ВС. Отрезок АН и есть искомый перпендикуляр к прямой ВС. В самом деле, при указанном наложении (перегибании рисунка) луч НА совмещается с лучом НА1, поэтому 1 совмещается с 2. Следовательно, 1=2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Итак, AHBC.
Обозначим буквой Н точку пересечения прямых АА1 и ВС. Отрезок АН и есть искомый перпендикуляр к прямой ВС. В самом деле, при указанном наложении (перегибании рисунка) луч НА совмещается с лучом НА1, поэтому 1 совмещается с 2. Следовательно, 1=2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Итак, AHBC. оказать: AD – медиана и высота.
оказать: AD – медиана и высота.


 сли две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
сли две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А совместилась с вершиной А1 сторона АВ — с равной ей стороной A1 B1, а вершины С и С1 оказались по одну сторону от прямой А1В1.
Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А совместилась с вершиной А1 сторона АВ — с равной ей стороной A1 B1, а вершины С и С1 оказались по одну сторону от прямой А1В1.


 риложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершина А совместилась с вершиной А1 вершина В — с вершиной В1 а вершины С и С1 оказались по разные стороны от прямой А1В1 (рис).
риложим треугольник АВС к треугольнику А1В1С1 так, чтобы вершина А совместилась с вершиной А1 вершина В — с вершиной В1 а вершины С и С1 оказались по разные стороны от прямой А1В1 (рис).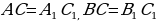 C=C1.
C=C1. кружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
кружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.




 остроить перпендикуляр к прямой
остроить перпендикуляр к прямой



 ано: АВС и А1В1С1;
ано: АВС и А1В1С1; 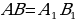 ;
; 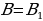
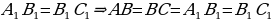
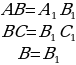 АВС = А1В1С1 (по2 сторонам и угла между ними).
АВС = А1В1С1 (по2 сторонам и угла между ними). ано: АВС – равнобедренный
ано: АВС – равнобедренный ано:
ано:  остройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой.
остройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой. остройте окружность данного радиуса, проходящую через две данные точки.
остройте окружность данного радиуса, проходящую через две данные точки. а стороне BC треугольника ABC Постройте точку, равноудалённую от вершин A и C.
а стороне BC треугольника ABC Постройте точку, равноудалённую от вершин A и C. рямая с называется секущей по отношению к прямым а и в, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
рямая с называется секущей по отношению к прямым а и в, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия: сли при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
сли при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. сли при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны
сли при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны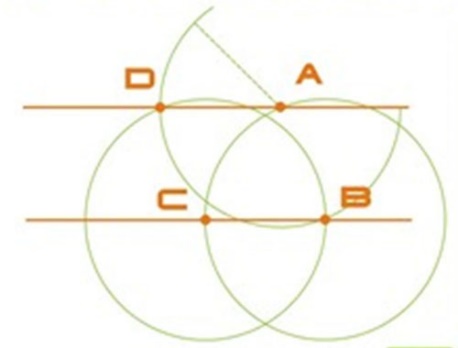 помощью циркуля и линейки:
помощью циркуля и линейки: 

 сли прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
сли прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
 ействительно, пусть прямые а и Ь параллельны прямой с (рис. а). Докажем, что а||b. Допустим, что прямые а и b не параллельны, т. е. пересекаются в некоторой точке М (рис. б). Тогда через точку М проходят две прямые (прямые а и b), параллельные прямой с.
ействительно, пусть прямые а и Ь параллельны прямой с (рис. а). Докажем, что а||b. Допустим, что прямые а и b не параллельны, т. е. пересекаются в некоторой точке М (рис. б). Тогда через точку М проходят две прямые (прямые а и b), параллельные прямой с.
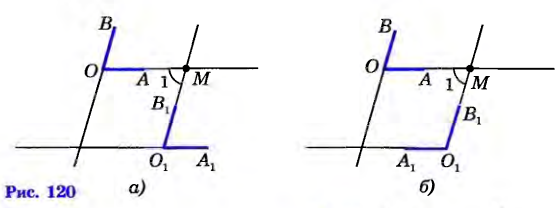 усть АОВ и А1О1В1 — данные углы и OA||O1A1, OB||O1B1. Если АОВ развернутый, то и А1О1В1 — развернутый (т.к. они лежат на параллельных прямых), поэтому эти углы равны. Пусть АОВ — неразвернутый угол. Возможные случаи расположения углов АОВ и А1О1В1 изображены на рисунке 120, а и б. Прямая О1В1 пересекает прямую и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М. Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов, образованных при пересечении прямых О1В1 и ОА (угол 1 на рисунке 120), равен углу АОВ (как накрест лежащие углы). Параллельные прямые ОА и ОА1 пересечены секущей О1М, поэтому либо 1=A1O1B1 (рис. 120, а), либо 1+ A1O1B1 = 1800 (рис. 120, б). Из равенства 1=AOB и последних двух равенств следует, что либо AOB=A1O1B1 (см. рис. 120, а), либо AOB + A1O1B1 =180° (см. рис. 120, б), что и требовалось доказать.
усть АОВ и А1О1В1 — данные углы и OA||O1A1, OB||O1B1. Если АОВ развернутый, то и А1О1В1 — развернутый (т.к. они лежат на параллельных прямых), поэтому эти углы равны. Пусть АОВ — неразвернутый угол. Возможные случаи расположения углов АОВ и А1О1В1 изображены на рисунке 120, а и б. Прямая О1В1 пересекает прямую и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М. Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов, образованных при пересечении прямых О1В1 и ОА (угол 1 на рисунке 120), равен углу АОВ (как накрест лежащие углы). Параллельные прямые ОА и ОА1 пересечены секущей О1М, поэтому либо 1=A1O1B1 (рис. 120, а), либо 1+ A1O1B1 = 1800 (рис. 120, б). Из равенства 1=AOB и последних двух равенств следует, что либо AOB=A1O1B1 (см. рис. 120, а), либо AOB + A1O1B1 =180° (см. рис. 120, б), что и требовалось доказать. ано:
ано: 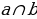 ;
; 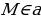
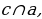 c||b
c||b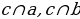 .
.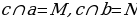
 Докажите, что если при пересечении двух прямых секущей накрест лежащие углы не равны, то данные прямые пересекаются.
Докажите, что если при пересечении двух прямых секущей накрест лежащие углы не равны, то данные прямые пересекаются. ано: АВС;
ано: АВС;  нешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
нешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. оказательство:
оказательство: аждая сторона треугольника меньше суммы двух других сторон.
аждая сторона треугольника меньше суммы двух других сторон.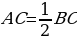 .
.  Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке. Получим треугольник BCD, в котором B=D=60°, поэтому DC=BC. Но
Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке. Получим треугольник BCD, в котором B=D=60°, поэтому DC=BC. Но 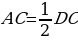 . Следовательно,
. Следовательно,  В=С1В1 то вершина В совместится с вершиной В1. Но тогда вершины А и А1 также совместятся. В самом деле, если предположить, что точка А совместится с некоторой другой точкой А2 луча А1А2, то получим равнобедренный треугольник А1В1А2 в котором углы при основании АгА2 не равны (A2 — острый, a A1 — тупой как смежный с острым углом
В=С1В1 то вершина В совместится с вершиной В1. Но тогда вершины А и А1 также совместятся. В самом деле, если предположить, что точка А совместится с некоторой другой точкой А2 луча А1А2, то получим равнобедренный треугольник А1В1А2 в котором углы при основании АгА2 не равны (A2 — острый, a A1 — тупой как смежный с острым углом 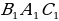 . Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А1В1С1, т. е. они равны. Теорема доказана.
. Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А1В1С1, т. е. они равны. Теорема доказана. усть отрезок АН — перпендикуляр, проведенный из точки А к прямой а, М — любая точка прямой а, отличная от Н (рис.). Отрезок AM называется наклонной, проведенной из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы AM. Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.
усть отрезок АН — перпендикуляр, проведенный из точки А к прямой а, М — любая точка прямой а, отличная от Н (рис.). Отрезок AM называется наклонной, проведенной из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы AM. Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой. ассмотрим параллельные прямые а и b. Отметим на прямой а точку А и проведем из этой точки перпендикуляр АВ к прямой b (рис.). Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.
ассмотрим параллельные прямые а и b. Отметим на прямой а точку А и проведем из этой точки перпендикуляр АВ к прямой b (рис.). Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.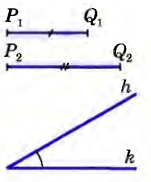 о двум сторонам и углу между ними
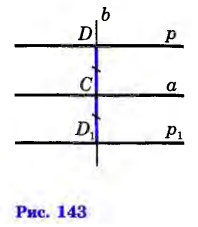
о двум сторонам и углу между ними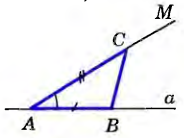 аны отрезки P1Q1 и P2Q2, и угол hk. Требуется с помощью циркуля и линейки (без масштабных делений) построить такой треугольник АВС, у которого две стороны, скажем АВ и АС, равны данным отрезкам P1Q1 и P2Q2, а угол А между этими сторонами равен данному углу hk.
аны отрезки P1Q1 и P2Q2, и угол hk. Требуется с помощью циркуля и линейки (без масштабных делений) построить такой треугольник АВС, у которого две стороны, скажем АВ и АС, равны данным отрезкам P1Q1 и P2Q2, а угол А между этими сторонами равен данному углу hk.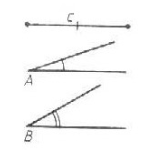
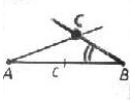 . Произвольно начертить отрезок АВ, равный заданному отрезку c.
. Произвольно начертить отрезок АВ, равный заданному отрезку c.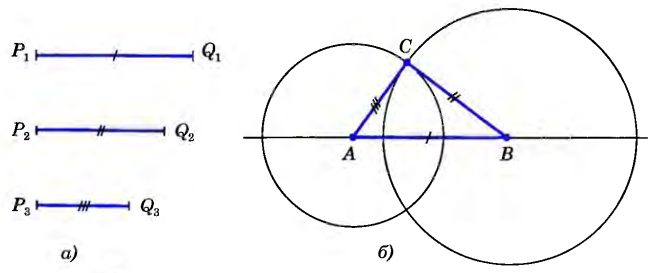 усть даны отрезки P1Q1 P2Q2 и P3Q3 (рис. а). Требуется построить треугольник АВС, в котором AB=P1Ql, BC=P2Q2, CA= P3Q3.
усть даны отрезки P1Q1 P2Q2 и P3Q3 (рис. а). Требуется построить треугольник АВС, в котором AB=P1Ql, BC=P2Q2, CA= P3Q3.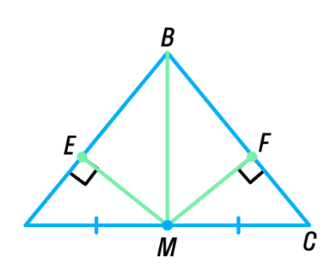 то представляет собой множество всех точек плоскости, находящихся на данном расстоянии от данной прямой?
то представляет собой множество всех точек плоскости, находящихся на данном расстоянии от данной прямой?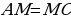 .
.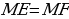 .
. 


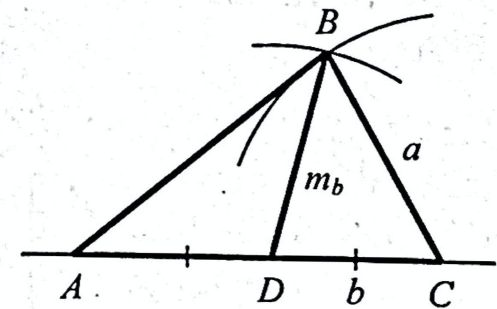 отрезок АС = b.
отрезок АС = b.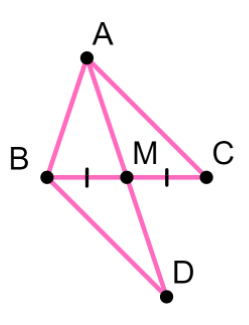 оказать:
оказать: 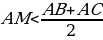
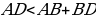 (по неравенству треугольника);
(по неравенству треугольника); 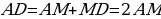 (по построению);
(по построению); 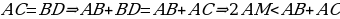
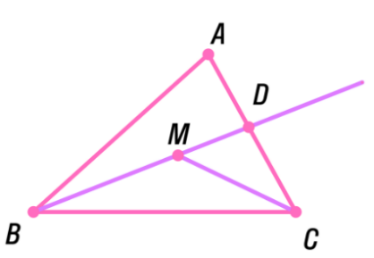 В + МС
В + МС 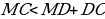 и
и 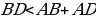
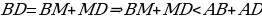
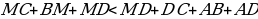
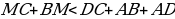
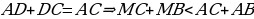 .
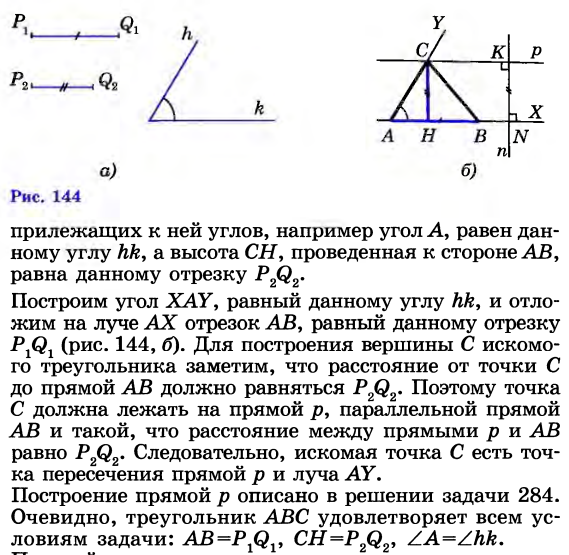
.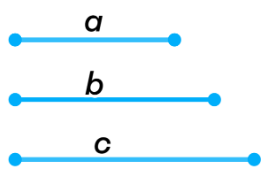 остройте треугольник по двум сторонам и медиане, проведённой к третьей стороне
остройте треугольник по двум сторонам и медиане, проведённой к третьей стороне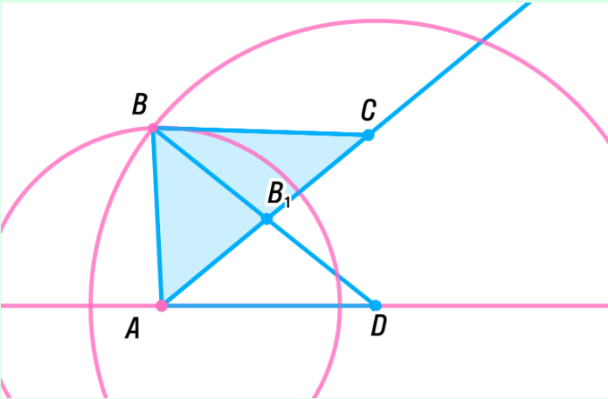 остроение:
остроение: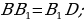 Проведем луч AB1.
Проведем луч AB1.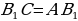
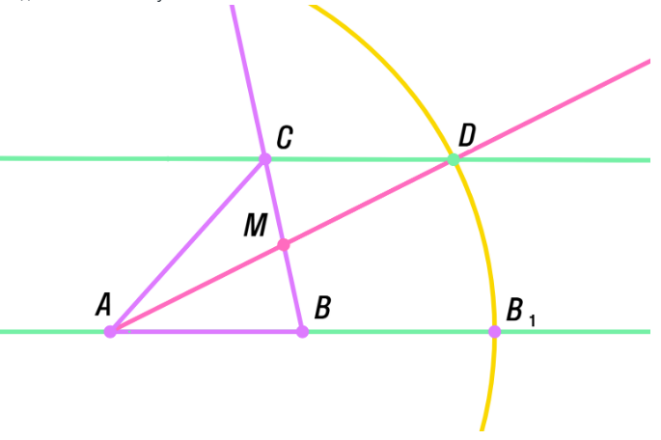 остроение:
остроение: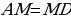
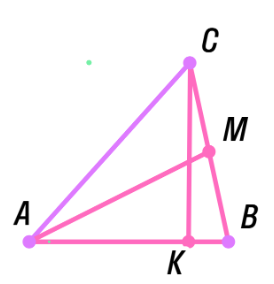 роведем луч ВМ и отметим точку С на пересечении с параллельной прямой m.
роведем луч ВМ и отметим точку С на пересечении с параллельной прямой m.













