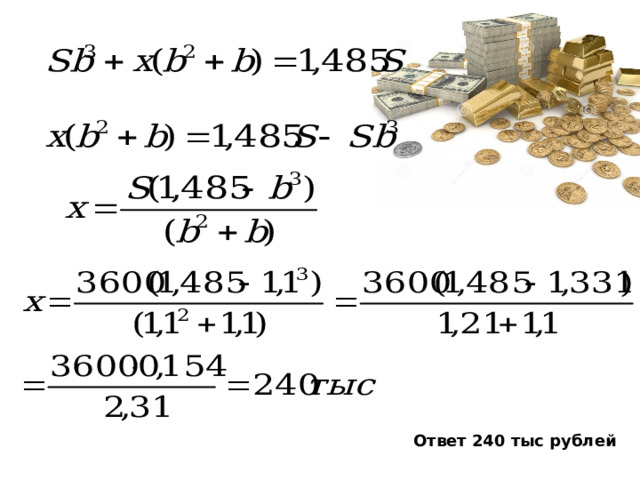Решение задач № 17. Банковские задачи.
Презентацию подготовила учитель математики МОУ ИРМО «Пивоваровская СОШ» Бочкарева Наталья Анатольевна


№ 1. 31 декабря 2013 года Алексей взял в банке 9930000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг тремя равными платежами (то есть за 3 года)?
Решение.
Пусть S = 9930000 р., a- процент банка, х – величина платежа
b = 1+ 0,01 а =1,1 – повышающий коэффициент ( то есть 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b )
Тогда:
31.12.2014 год: ( Sb – X ) –(сумма долга после первой выплаты)
31.12.2015 год: - сумма долга после второй выплаты
31.12.2016 год: - сумма долга после третьей выплаты

Выразим Х
Ответ: 3663000

№ 2 .
Решение.
Пусть S – сумма кредита, a – годовой %, b=1+0,01 a , Х 1 =328050 р., Y =587250
Рассчитаем кредит на 4 года:
31.12.2015: ( Sb – X )
31.12.2016: ( Sb – X)b – X
31.12.2017:
31.12.2018:

№ 2 .
Рассчитаем кредит на 2 года:
31.12.2015: ( Sb – Y )
Исключим S и выразим b
31.12.2016: ( Sb – Y)b – Y =0
Ответ: 12,5%

3. Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?
Решение.
Пусть S = 360000 р., a =10% - процент банка, х – величина дополнительного вклада
b = 1+ 0,01 а =1,1 – повышающий коэффициент ( то есть 31 декабря каждого года оставшаяся сумма вклада умножается на коэффициент b )
Тогда:
первый год: ( Sb + X ) –(сумма вклада после первой выплаты)
второй год: - сумма вклада после второй выплаты
Третий год: - сумма вклада после третьей выплаты
Составим уравнение
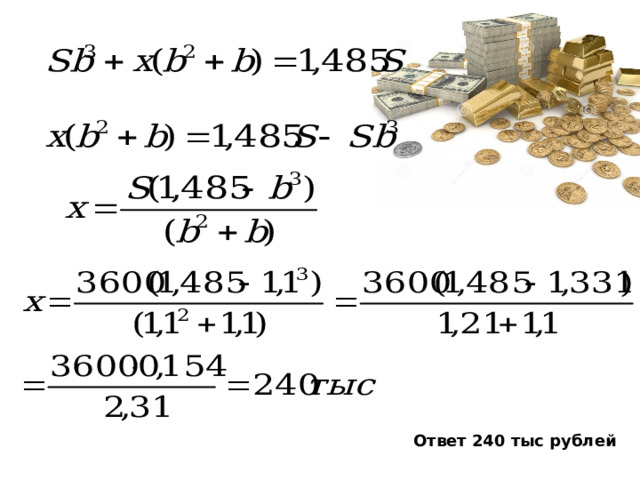
Ответ 240 тыс рублей

№ 3. 1 января 2015 года Александр Сергеевич взял в банке 1,1 млн.рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга, затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс.рублей.?
Решение: 1 способ
1.01.2015 : взял 1,1 млн.руб
1.02.2015: 1,1 млн.-275000=725100 руб,
после начисления 1% : 725100+7251=732351 руб.
1.03.2015: 732351-275000=457351 руб.
после начисления 1% : 457351+4573,51=461924,51 руб.
1.04.2015: 461924,51-275000=186924,51 руб.
после начисления 1%:
186924,51+1869,2451=188793,7551 руб.
1.05.2015: 188793,7551 275000,
следовательно Александр Сергеевич
закрывает кредит.
Ответ: 5 месяцев

№ 3. 1 января 2015 года Александр Сергеевич взял в банке 1,1 млн.рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга, затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс.рублей.?
2 способ
Выплачивая каждый месяц 275 тыс рублей на погашение основного долга 1,1 млн рублей потребуется 1,1:0,275=4 месяца. Посчитаем проценты банка за 4 месяца:
1 месяц: 1,1∙0,01=11 тыс рублей
2 месяц: менее 11 тыс рублей и т. д.
За 4 месяца: 44 тыс
Следовательно на погашения
всего долга нужно 5 месяцев
Ответ: 5 месяцев