Наибольшее и наименьшее значение функции на отрезке

ПЛАН ЗАНЯТИЯ № 100

Дисциплина Математика

Специальность

Курс 1 группа C 153

Тема занятия: Наибольшее и наименьшее значение функций

Тип урока: урок закрепления знаний и формирование умений и навыков

Вид занятия: практическое занятие

Цели:

– обучающая: Составить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке. Провести первичное закрепление и первичный контроль усвоения алгоритма;

– развивающая: Развивать логическое мышление, вычислительные навыки;

– воспитательная: содействовать воспитанию у студентов самостоятельности, самопознания, самосозидания и самореализации.

Задачи:

- должен знать: нахождение наибольшего и наименьшего значений функции

- должен уметь: применять полученные знания на практике

Формируемые компетенции:

– общие: ОК 1-9

– профессиональные: ПК 1.1. – ПК 4.3.

Обеспечение занятия: карточки, ОК

Внутридисциплинарные связи: занятие по теме «Наибольшее и наименьшее значения функции» связано с такими темами как: «Определение производной ее геометрический и физический смысл», «Производные основных элементарных функций», «Вторая производная, ее физический смысл», «Нахождение скорости и ускорения с помощью производной», «Дифференцирование сложных функций», «Признак постоянства, возрастание и убывание функции», «Экстремумы функции. Исследование функции на экстремум», «Исследование функции с помощью производной», «Применение производной к построению графиков», «Применение производной к исследованию и построению функций», «Выпуклость графика функции, точки перегиба», «Решение упражнений по теме: «Производная и ее приложение»

Методы обучения: активные: словесные, наглядные

Ход занятия

1. Организация занятия (3 мин.).

2. Сообщение темы и целей занятия. (4 мин.)

3. Актуализация опорных знаний как переход к освоению новых знаний. (7мин.)

Для изучения новой темы нам необходимо повторить пройденный материал. Сделаете вы это, выполнив устно следующие задания. В тетрадь запишите только ответы к каждому пункту. (3мин.)

По графику функции у=f(x) найдите:

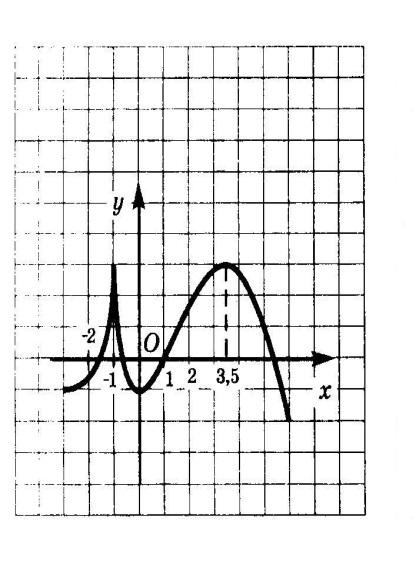
1.Область определения функции.

[-3;6]

2. Абсциссы точек, в которых f`(x)=0

0;3,5

3. Абсциссы точек, в которых f`(x) не существует.

-1

4. Наибольшее значение функции. (Унаиб.).

Унаиб=3

5. Наименьшее значение функции (Унаим.).

Унаим.=-2

Преподаватель: Какие точки называются стационарными?

Обучающийся: Стационарными называются точки, в которых производная функции f^/ (x)=0.

Преподаватель: Чтобы найти стационарные точки надо: найти производную функции f^/ (x) и решить уравнение f^/ (x)=0

1. Сообщение и усвоение новых знаний с закреплением полученных знаний. (41 мин.)

Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]

1. найти f '(x);

2. найти точки, в которых f '(x)=0 или f '(x) не существует, и отобрать из них те, что лежат внутри отрезка [a;b];

3. вычислить значения функции y=f '(x) в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f(x) на отрезке [a;b], которые можно обозначить так: max y(x) и min y(x).

[a;b] [a;b]

Пример.

Найдем наибольшее и наименьшее значения функции на отрезке .

Найдем критические точки.

Так как производная функции определена для любого х, решим уравнение

Ответ.

1. Закрепление нового материала. Решение задач.

1 Вариант.

Найдите У наиб. и У наим. Функции у=2-8x+6 на отрезке[-1;4]

Решение

Д(у)=

1.у´=

2. Д(у´)=

Найди стационарные точки, решив уравнение у´=0

Отбери точки, принадлежащие отрезку [-1;4]

3. Найди у(-1)

У(4)

И в отобранных точках на втором шаге

Отбери среди найденных значений наибольшее и наименьшее.

Ответ

У наиб=

У наим.=

2 Вариант.

Найдите У наиб. и У наим. Функции у=+4x-3 на отрезке

[-3;2]

Решение

Д(у)=

1.у´=

2. Д(у´)=

Найди стационарные точки, решив уравнение у´=0

Отбери точки, принадлежащие отрезку [-3;2]

3. Найди у(-3)

У(2)

И в отобранных точках на втором шаге

Отбери среди найденных значений наибольшее и наименьшее.

Ответ

Унаиб=

Унаим.=

Решение задания из учебника

Самостоятельная работа

Вариант 1. Определите наибольшее и наименьшее значения функции у= х² + 4x на отрезке [-3;6].

Варианты ответа:

а) min y(x)= -12, max y(x)= -5; б) min y(x)= -4, max y(x)= 60; в) min y(x)= -12, max y(x)= 4

[-3;6] [-3;6] [-3;6] [-3;6] [-3;6] [-3;6]

Вариант 2. Определите наибольшее и наименьшее значения функции у= х²-2х на отрезке [1/2;4].

Варианты ответа:

а) min y(x)= -1, max y(x)= -3/4; б) min y(x)= -1, max y(x)= 8; в) min y(x)= -3/4, max y(x)= -1

[1/2;4] [1/2;4] [1/2;4] [1/2;4] [1/2;4] [1/2;4]

Вариант 3. Определите наибольшее и наименьшее значения функции у= 3х² + 6x на отрезке [-2;2].

Варианты ответа:

а) min y(x)= -4, max y(x)= 0; б) min y(x)= -20, max y(x)= 0; в) min y(x)= -3, max y(x)= 24

[-2;2] [-2;2] [-2;2] [-2;2] [-2;2] [-2;2]

Вариант 4. Определите наибольшее и наименьшее значения функции у= 2х²- 2х на отрезке [-1;3].

Варианты ответа:

а) min y(x)= -0,5, max y(x)= 12; б) min y(x)= 4, max y(x)= 5; в) min y(x)= 0, max y(x)= 5

[-1;3] [-1;3] [-1;3] [-1;3] [-1;3] [-1;3]

1. Подведение итогов занятия. (5 мин.)

Чем мы занимались сегодня на уроке?

Что понравилось, какие виды деятельности?

Анализ работы студентов, выставление оценок

1. Рефлексия занятия. (5 мин.)

Продолжите предложения:

- Я сегодня узнал…

- Мне была интересна задача…

- Самая сложная задача для меня заключалась…

- Мне занятие понравилось….

- Мне занятие не понравилось…

1. Задание для внеаудиторной самостоятельной работы. (5 мин.)

Параграф 52, № 938