Урок алгебры и начал математического анализа в 11а классе
2018-2019 учебный год. 11.12.2018г.
(изучение математики на базовом уровне)
Учитель Жужукина И.А.
Тема урока Наибольшее и наименьшее значение функции на отрезке.
Тип урока Комбинированный
Цель урока Организация продуктивной деятельности школьников, направленной на достижение ими следующих результатов:
личностных
метапредметных
-
обеспечить развитие у школьников умения ставить цель и планировать свою деятельность;
-
содействовать развитию у обучающихся умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.
предметных
обучающиеся научатся:
-
понятие наибольшего и наименьшего значения функции на отрезке;
-
алгоритм вычисления наибольшего и наименьшего значения функции на отрезке;
-
применять изученный алгоритм при решении упражнений;
-
продолжить работу по формированию умения проводить исследование непрерывной функции y=f(x) на монотонность и экстремумы.
обучающиеся получат возможность научиться:
Ход урока
Этап 1. Актуализация знаний (вхождение в тему урока и создание условий для осознанного восприятия нового материала)
Устные задания по типу ЕГЭ (базовый уровень)
Задание № 1 (Задание 14 № 506377 Решу ЕГЭ) (Слайд 1)
На рисунке изображён график функции y = f(x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику функции или её производной.
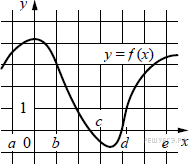
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) | | 1) производная отрицательна на всём интервале 2) производная положительна в начале интервала и отрицательна в конце интервала 3) функция отрицательна в начале интервала и положительна в конце интервала 4) производная положительна на всём интервале |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Задание № 2 (Задание 14 № 506286 решу ЕГЭ) (Слайд 2)
На рисунке изображён график функции, к которому проведены касательные в четырёх точках.
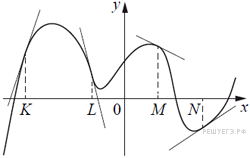
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А) K Б) L В) M Г) N | | 1) −4 2) 3 3)  4) −0,5 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Этап 2. Организация и самоорганизация учащихся в ходе изучения нового материала
1) Водная беседа учителя. Постановка перед учащимися учебной проблемы.
Человек, приступающий к осуществлению своих мероприятий, всегда пытается принимать оптимальные решения. Многие решения могут приниматься без специального математического анализа, просто на основе опыта и здравого смысла.
Возьмем пример: человек вышел утром из дому, чтобы ехать на работу. По ходу дела ему приходится принять целый ряд решений: брать ли с собой зонтик? В каком месте перейти улицу. И так далее.
С задачами, требующими оптимального решения, в наше время приходится иметь дело представителям самых разных специальностей. Технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д. Решение таких задач опирается на точные математические расчеты. Задачи подобного рода носят общее название – задачи на оптимизацию (от латинского слова optimum – “наилучший” – (Слайд 3).
В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причём надо найти такое значение второй величины, при котором первая принимает своё наименьшее или наибольшее (наилучшее в данных условиях) значение. Учиться решать такие задачи мы будем решать на последующих уроках, а сегодня попробуем отыскать алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.
2) Давайте рассмотрим различные варианты поведения непрерывной на отрезке функции, и попытаемся определить, в каких точках она достигает своего наибольшего и наименьшего значений.
Обсуждение в группах по предложенному плану. Обмен мнениями. Фиксация выводов. (Слайд 4, 5. 6)
План обсуждения слайдов.
-
В какой точке функция достигает своего наибольшего значения?
-
В какой точке функция достигает своего наименьшего значения?
-
Чем можно сказать о данных точках отрезка [a;b]?
-
Какой вывод можно сделать?
3) Проанализируйте все рассмотренные случаи, установите закономерности нахождения наибольшего и наименьшего значения функции на отрезке.
Беседа по слайду:
Выводы:
1. Если функция у = f(х) на отрезке [а; b] имеет лишь одну точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
2. Если функция у = f(х) на отрезке [а; b] не имеет стационарных точек , то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает одном конце отрезка, а наименьшее – на другом.
3. Если на отрезке [а; b] функция имеет несколько стационарных точек, то своего наибольшего (наименьшего) значения она достигает либо на концах этого отрезка, либо в стационарных точках, лежащих на данном отрезке.
4) Составить алгоритм и сравнить его с алгоритмом, предложенным в учебнике. (Слайд 7)
5) Работа с образцом решения упражнения. Фронтальное повторение основных этапов решения с опорой на слайд (Слайд 8)
Этап 3. Первичное закрепление изученного материала.
А) Решение упражнения. Найти наибольшее значение функции
f (x) = x3 – 3x2 + 3x + 2 на отрезке [– 2; 2].
Б )Как можно изменить условие задания, чтобы получить несколько вариантов заданий подобного типа?
.
В) Как вы думаете, можно ли по графику производной определить, в какой точке функция принимает наибольшее ( наименьшее) значение? ( Работа со слайдом 9)
Этап 4. Применение алгоритма нахождения наибольшего наименьшего значения функции при решении задач ЕГЭ.
Традиционно задачи, связанные с нахождением наибольшего и наименьшего значения функции на отрезке включаются в ЕГЭ. Это задание № 12 профильного уровня.
Образцы заданий: (Слайд 10)
Найдите наибольшее значение функции 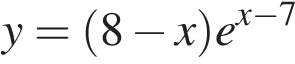 на отрезке
на отрезке 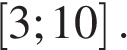
Найдите наименьшее значение функции 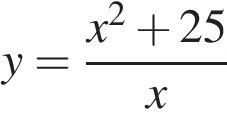 на отрезке
на отрезке 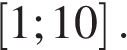
Найдите наименьшее значение функции 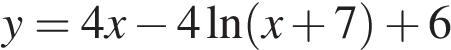 на отрезке
на отрезке 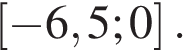
Найдите наименьшее значение функции 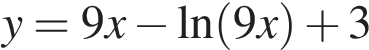 на отрезке
на отрезке 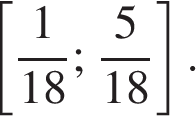
Найдите наибольшее значение функции 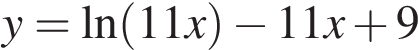 на отрезке
на отрезке 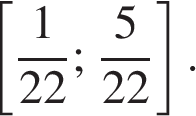
Найдите наибольшее значение функции 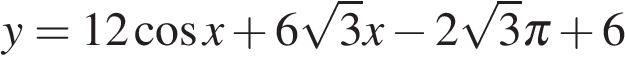 на отрезке
на отрезке 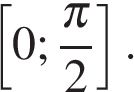
Найдите наименьшее значение функции 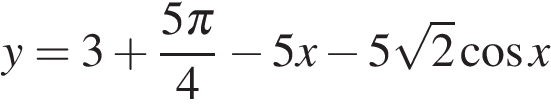 на отрезке
на отрезке 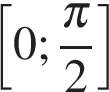 .
.
Этап 5. Рефлексия. Организация обратной связи.
1)Самостоятельная работа.
Вариант 1. Задание 12 № 77421
Найдите наименьшее значение функции 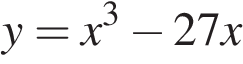 на отрезке
на отрезке 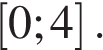
Вариант 2. Задание 12 № 77426
Найдите наибольшее значение функции 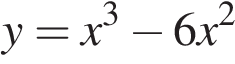 на отрезке
на отрезке 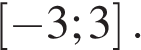
Проверка по Слайду 11,12
2) Задание на дом : глава 3,п.3, №281-283
Этап 6. Анализ работы обучающихся на уроке, выставление отметок
.
Анализ урока
алгебры и начал математического анализа в 11А классе 11.12.2018 г. по теме Наибольшее и наименьшее значение функции на отрезке.
Учитель Жужукина И.А.
1.Организационный момент
Подготовка учащихся к работе на уроке.. Несколько учащихся опоздали на урок.
2. Подготовка к основному этапу урока
Совместное формулирование целей урока для учащихся для определения действий школьников во время урока; обеспечение осознания учащимися необходимости изучения новой темы – ссылка на задание № 12 ЕГЭ профильный уровень.
Актуализация опорных знаний и умений по теме «Применение производной» - задания по типу ЕГЭ базовый уровень –по готовым графикам (слайды на электронной доске).
Создание поискового режима для подготовки и восприятия содержания нового материала с помощью работы над предложенными графиками. Учащиеся 9примерно 50% класса) активно работают. Грамотно и обоснованно отвечают на вопросы учителя при фронтальной беседе.
Указаны планируемые результаты, чётко поставлены образовательные и развивающие цели, сформулированные вместе с учащимися в их действиях, но нет чёткости в постановке воспитательных целей. Обеспечена мотивация и принятие учащимися целей урока. Осознанное и быстрое включение школьников в деловой ритм. Готовность учащихся к активной учебно-познавательной деятельности на основе повторенных опорных знаний и проведённой поисковой работы.
3. Изучение нового материала
Перед учащимися поставлена конкретная учебная цель – вывести алгоритм решения заданий на нахождение наибольшего и наименьшего значений функции на отрезке. Организована фронтальная работа с классом с применением готовых слайдов на электронной доске. Ученики выводят алгоритм выполнения заданий подобного типа. Сверяют его с правилом из учебника. Рассматривают предложенный образец письменного оформления задания и образцы заданий №12 из Каталога ЕГЭ, намечая таким образом ближайшие перспективы изучения темы на последующих уроках.
4. Закрепление изученного материала - решение заданий на исследование степенных функций с опорой на выведенный алгоритм на доске и в тетрадях учащихся .
Самостоятельная работа обучающего характера, задания на нахождение наибольшего и наименьшего значений степенных функций на отрезке (задания взяты из Каталога заданий ЕГЭ профильный уровень). Проверка с помощью электронной доски, 60% учащихся не довели исследование до конца.
5. Рефлексия. Подведение итогов урока. Задание на дом – разъяснение учащимся критериев успешного выполнения домашнего задания.





























