Муниципальное бюджетное общеобразовательное учреждение
Сарсак-Омгинский лицей
Агрызского муниципального района
Республики Татарстан
ПРОЕКТНАЯ РАБОТА
Предмет: МАТЕМАТИКА
Тема: «Обыкновенные дроби вокруг нас»
ФИО обучающегося, класс:
Халитова Александра Дмитриевна, 5 класс
Руководитель: Маркитонова Людмила Леонидовн
Май 2019
Цель проекта:
Изучение понятия « дробь», его многозначности и применение в окружающей нас жизни и в математике.
Задачи
Узнать, где человек встречается с понятием «дробь» в жизни;
Узнать историю возникновения дробей в математике;
Выяснить необходимость использования математических дробей в повседневной жизни
Найти примеры использования дробей в литературе и искусстве .
Старинные задачи с дробями.
Занимательная страничка. Кроссворды, ребусы и т.д.
Основополагающий вопрос:
Может ли существовать человек без дробей?
Проблемные вопросы
Объект исследования – математика.
Предмет исследования – обыкновенные дроби.
При работе над проблемой мы пользовались следующими методами:
анкетирование и обработка данных (до и после исследования);
поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;
наблюдение;
анализ полученных в ходе исследования данных.
Что же такое дробь?
В толковом словаре это слово имеет несколько значений.
собир. Мелкие свинцовые шарики для стрельбы из охотничьего ружья. Зарядить ружьё дробью. Стрелять мелкой дробью. Вложить в ружьё заряд дроби.
Частые, ритмически повторяющиеся звуки от ударов по чему-либо. Дробь дождя, града. Слышна сухая дробь пишущих машинок. Барабанная дробь. Отбивать дробь. (о барабанщике).
Танцевальная дробь. Весёлая дробь чечётки.
Выбивать дробь зубами – стучать зубами (дрожа от холода, испуга и т. п.).
В доме восемь дробь 1 жил высокий господин.
Номер через дробь ставят у домов, пронумерованных по двум пересекающимся улицам.
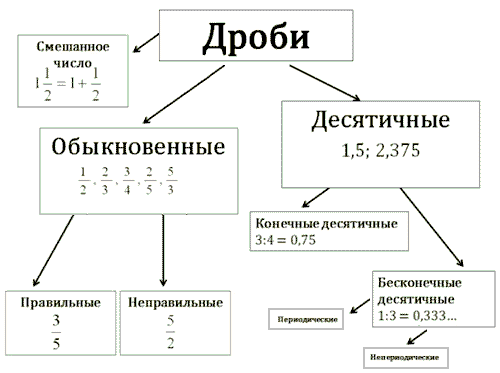
Математика: Число, состоящее из частей единицы. Обыкновенные дроби. Десятичные дроби. Правильные и неправильные дроби, сложение, вычитание дробей.
Обыкновенная дробь называется правильной, если её числитель меньше её знаменателя. Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя.
Правильная дробь меньше единицы, а неправильная дробь больше или равна единице.
Как возникли дроби в математике?
В повседневной жизни мы часто сталкиваемся с такими понятиями, как половина, треть, четверть. А это ведь тоже дроби. С самого детства мы слышим такие выражения: "весит четверть килограмма", "одна вторая листа" или "три четверти часа". Во всех этих случаях мы говорим о дробях: одна четверть, две четверти, три четверти, одна вторая и треть - все это дроби. Люди разных профессий используют дроби в процессе работы, даже не задумываясь об этом. Например, врач, назначая количество лекарства больному, повар, отмеряя необходимые ингредиенты, продавец, водопроводчик, слесарь и даже музыкант. Да и мы пользуемся дробями с самого детства, не подозревая об этом ("Мама, дай мне половинку яблока", "Давай разделим шоколадку поровну", "Я еще четверть часика поиграю в компьютер").
Как же возникла необходимость в обыкновенных дробях? Откуда они взялись, как, когда, где и кто начал изучать дроби? Как записывали и использовали дроби в разные времена и в разных странах? В школьных учебниках нет информации на данную тему. А зачем изучать действия с дробями, если мы, не знаем, нужны ли они нам?
.
Из истории возникновения обыкновенных дробей.
Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.
Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.
Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.
В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
Дроби в Древнем Египте
В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
В Древнем Египте некоторые дроби имели свои особые названия – а именно, часто возникающие на практике 1/2, 1/3, 2/3, 1/4, 3/4, 1/6 и 1/8. Кроме того, египтяне умели оперировать с так называемыми аликвотными дробями (от лат. aliquot – несколько) типа 1/n – их поэтому иногда также называют «египетскими»; эти дроби имели свое написание: вытянутый горизонтальный овальчик и под ним обозначение знаменателя. Что касается остальных дробей, то их следовало раскладывать в сумму египетских. Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа - 2/3 - у них был специальный значок. Это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица - все остальные дроби непременно имели в числителе единицу (так называемые основные дроби). Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно. Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением. Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи.
Дроби в Древней Греции
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков (к примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой). Максим Плануд греческий монах, ученый, математик в 13 веке ввел название числителя и знаменателя
В Греции употреблялись наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним – числитель дроби. Например, означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями.
Дроби в Индии.
Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (a + b/c) или деление целого числа a на дробь b/c. Правила действий над дробями почти не отличались от современных.
 Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
Вначале в записи дробей не использовалась дробная черта.
Черта дроби появилась лишь только в 1202 году у итальянского математика Леонардо Пизанского. Он ввел слово дробь.
 Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик. Записывать дроби как сейчас стали арабы.
Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик. Записывать дроби как сейчас стали арабы.
Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть.
Дроби на Руси
В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находим следующие названия дробей на Руси:
| 1/2 - половина, полтина | 1/3 – треть |
| 1/4 – четь | 1/6 – полтреть |
| 1/8 - полчеть | 1/12 –полполтреть |
| 1/16 - полполчеть | 1/24 – полполполтреть (малая треть) |
| 1/32 – полполполчеть (малая четь) | 1/5 – пятина |
| 1/7 - седьмина | 1/10 - десятина |
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
Живя в окружении дробей, мы не всегда их явно замечаем. И все же, мы сталкиваемся с ним очень часто: дома, на улице, в магазине, на работе и так далее. Мы покажем лишь малую часть того, где мы можем увидеть присутствие дробей.
На основе исследования истории возникновения обыкновенных дробей, мы задались вопросом:
Для ответа на поставленный нами вопрос мы решили опросить родителей, знакомых и учителей о том, где используются обыкновенные дроби в быту и в работе людей разных профессий.
После опроса мы проанализировали полученные данные:
Ответы родителей:
деление на части использует портной при раскрое одежды. Когда одежда уже готова, мы видим рукав длины три четверти- ¾ или брюки длины 7/8 ;
сварщикам дроби нужны для измерения длины сваренной трубы и ширины сварочного шва.
дроби в медицине: чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или когда врач назначает больному ½ таблетки
повара для составления применяют дроби меню.
парикмахер применяет дроби для приготовления раствора для покраски волос и для завивки.
в кулинарии при приготовлении блюд по рецептам.
в магазине при взвешивании товара.
экономисты и бухгалтеры используют десятичные дроби для составления отчетов, расчетов.
в спорте - когда смотрим ½ финала матча по футболу;
при сравнении единиц длины: в английской системе мер
1 дюйм = 1/12 фута = 1/36 ярда или в Японии: 1 сун = 1/33 м;
при измерении времени: 30 минут=1/2 часа, 15 минут=1/4 часа, 40 минут=2/3 часа или без четверти час – без 20 минут час;
при приготовлении бетонной смеси : цемент -1 часть, щебень 4 части, песок - 2 части, вода - 1/2 части.
Ответы учителей:
дроби используются в первую очередь на уроках математики, с целью обучения ребят тому, как обращаться с дробями, где их использовать на практике в жизни;
в музыке: Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями. Выполняя сложение и вычитание дробей люди стали указывать размер такта. 
Масштаб карты равен 1/50000. Вода покрывает более 7/10 поверхности земного шара. По разным подсчётам доля пресной воды в общем количестве воды на Земле составляет 3/100. Около 87/100 запасов пресной воды содержится в виде льда
в химии - молекула воды Н2О состоит из двух частей водорода;
на биологии: пропорции человека тоже связаны с дробями; Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».
в юридической деятельности - Попробуйте решить следующую задачку: Наследники А. Б. В получили в наследство каждый по завещанию: А. – 1/8 имущества наследодателя; Б. – 6/17; В. - завещано всё остальное. Какие доли достались каждому из наследников?
Изучив историю возникновения дробей, и исследовав области применения дробей, мы доказали, что
Дроби нашли широкое применение в окружающей нас жизни и в различных науках;
Значение дроби в жизни очень велико. С их помощью строят дома, лечат людей, измеряют время, пишут музыку и шьют одежду… Значение дробей трудно переоценить.

Закончить своё выступление хочется словами выдающегося римского оратора и писателя Цицерона, жившего в первом веке до нашей эры. Он говорил:
“Без знания дробей никто не может признаваться знающим арифметику!”.
Итогом нашей работы стал выпуск ЛЭП бука по теме «Обыкновенные дроби»
ЛИТЕРАТУРА
1. Депман И. Я. Мир чисел. М.: Детская литература,1982
2. Дорофеева А. В. Страницы истории на уроках математики: книга для учителя. — М.: Просвещение, 2007.
3.Кординский Б. А.,Ахадов Л. А. Удивительный мир чисел: книга для учащихся. М.Просвещение,1986.
4.Толковый словарь.
4. Интернет ресурсы:







 Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
Народы прошли через многие варианты записи дробей, пока не пришли к современной записи. Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик. Записывать дроби как сейчас стали арабы.
Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик. Записывать дроби как сейчас стали арабы.













