Вариант 1
1. Квадрат каждого из трех данных чисел равен произведению двух оставшихся чисел. Докажите, что все данные числа равны.
2. В каком году XX века родился человек, если в 1997 году произведение цифр лет, прожитых им, уменьшенное в 4 раза, на 3 меньше суммы цифр года его рождения?
3. Построить график функции y = | x2 – 1 | – | x2 – 9 |.
4. Периметр треугольника равен 24 см. Можно ли около этого треугольника описать окружности радиусом 5 см?
5. Докажите, что при любом значении x выполняется равенство:
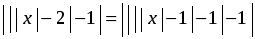 .
.
6. Трава на лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы ее за 24 дня, а 30 коров – за 60 дней. Сколько коров съели бы всю траву за 96 дней?
1. Пусть a, b, c – данные числа.
По условию имеем a2 = bc; b2 = ac; c2 = ab. умножим эти равенства на a, b, c соответственно получим, что a3 = b3 = c3 = abc, но если равны кубы чисел, то равны и сами эти числа.
2. 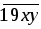 – год рождения.
– год рождения.
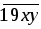 = 1000 + 9 ∙ 100 + 10x + y,
= 1000 + 9 ∙ 100 + 10x + y,
1997 – (100 + 9 ∙ 100 + 10x + y) = 10 ∙ (9 – x) + (7 – y) – возраст 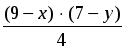 + 3 = 1 + 9 + x + y, откуда y =
+ 3 = 1 + 9 + x + y, откуда y = 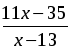 .
.
Единственное решение в целых числах: x = 1; y = 2.
Необходимо рассмотреть 2-й случай, когда y 7, тогда
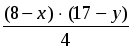 + 3 = 1 + 9 + x + y, откуда
+ 3 = 1 + 9 + x + y, откуда
x = 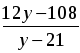 ; y = 9; x = 0.
; y = 9; x = 0.
Ответ: 1912 год, 1909 год.
3. y = | x2 – 1 | – | x2 – 9 | преобразовать к виду кусочно-заданной функции и построить график
y = f (x) = 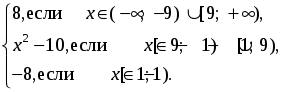
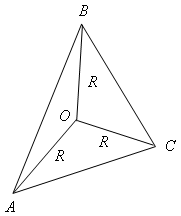
4. Пусть ∆ABC – некоторый треугольник и О – центр описанной около него окружности с радиусом R.
Тогда AB R; BC R; AC R; P∆ABC R 24
5. Можно построить графики обеих частей уравнения, используя преобразование графиков функций, возможно аналитическое решение уравнения, но тогда потребуется рассмотрение 6 случаев возможного значения переменной x.
6. 20 коров.
Пусть было на лугу A кг травы и растет она со скоростью x кг в день. Одна корова съедает y кг травы в день, получаем следующую систему:
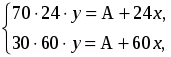
а необходимо найти такое число z, что 96 ∙ z ∙ y = A + 96x. Используя систему уравнений, получим, что z = 20.
Вариант 2
1. Упростить выражение 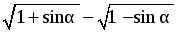 , где 0°
, где 0°
2. Вычислить a4 + b4 + c4, зная, что a + b + c = 0 и a2 + b2 + c2 = 1.
3. Найти сумму целых решений неравенства: 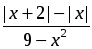 ≥ 0.
≥ 0.
4. Точки P, K, M, N – соответственно середины сторон AB, BC, CD, DA выпуклого четырехугольника ABCD. Отрезки AK и CP пересекаются в точке F, отрезки AM и CN – в точке E. Площадь четырехугольника AFCE равна 666. Найдите площадь четырехугольника ABCD.
5. Найдите площадь фигуры, заданной неравенством:
| x – 5 | + | y + 9 | ≤ 4.
6. Решить систему уравнений: 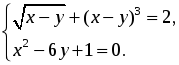
1. 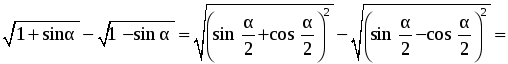
= 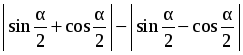 = sin
= sin 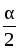 + cos
+ cos 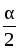 + sin
+ sin 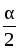 – cos
– cos 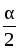 =
=
= 2sin 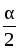 ;
;
0°
0°
2. (a2 + b2 + c2)2 = 12;
a4 + b4 + c4 + 2a2b2 + 2a2c2 + 2b2c2 = 1;
(a + b + c)2 = 02;
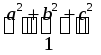 + 2ab + 2bc + 2ac = 0;
+ 2ab + 2bc + 2ac = 0;
ab + bc + ac = 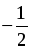 ;
;
(ab + bc + ac)2 = 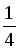 ;
;
a2b2 + b2c2 + a2c2 + 2acb2 + 2a2bc + 2bac2 = 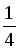 ;
;
a2b2 + b2c2 + a2c2 + 2abc (a + b + c) = 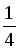 ;
;
a2b2 + b2c2 + a2c2 = 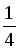 ;
;
2a2b2 + 2b2c2 + 2a2c2 =  , имеем, что
, имеем, что
a4 + b4 + c4 +  = 1 a4 + b4 + c4 =
= 1 a4 + b4 + c4 =  .
.
Ответ: a4 + b4 + c4 =  .
.
3. 2.
4. 1998.
5. Фигура представляет собой квадрат с центром в точке (5; –9) и диагональю, равной 8, поэтому площадь равна  = 32.
= 32.
6. Обозначим  = t, причем t ≥ 0;
= t, причем t ≥ 0;
t + t6 = 2; t6 + t – 2 = 0; t = 1 – корень данного уравнения.
(t – 1) ∙ (t5 + t4 + t3 + t2 + t + 2) = 0, значит, x = y, откуда
то есть y2 – 6y + 1 = 0.
y1 = 3 + 2 ; x1 = 3 + 2
; x1 = 3 + 2 ;
;
y2 = 3 – 2 ; x2 = 3 – 2
; x2 = 3 – 2 .
.
Ответ: (3 + 2 ; 3 + 2
; 3 + 2 ); (3 – 2
); (3 – 2 ; 3 – 2
; 3 – 2 ).
).
Вариант 3
1. Вычислить , если tg = 2.
2. Решите систему уравнений
3. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором
AB = AA1 = 12, AD = 30. Точка М расположена на грани ABB1A1 на расстоянии 1 см от середины AB и на равных расстояниях от A и B. Точка N принадлежит грани DCC1D1 и расположена симметрично точке М относительно центра параллелепипеда. Найти длину кратчайшего пути по поверхности параллелепипеда между точками М и N.
4. Из точки Е к окружности диаметром KМ проведена касательная ЕМ. Отрезок ЕK пересекается с окружностью в точке D, ED = 2 дм; KМ = 6 дм. Найдите градусную меру дуги окружности, заключенной внутри ∆MEK.
5. Найдите сумму 1 + 11 + 111 + 1111 + ... + 11...1 (всего 2000 слагаемых).
6. Решить графически систему уравнений:
1. 1 .
.
2.
Решим первое уравнение системы относительно x.
 = (y + 19)2 – 50y2 + 60y – 410 = –49y2 + 98y – 49 =
= (y + 19)2 – 50y2 + 60y – 410 = –49y2 + 98y – 49 =
= –49 (y2 – 2y + 1) = –49 (y – 1)2.
Очевидно, что уравнение имеет решение лишь при y = 1; найдем x:
10x2 – 40x + 40 = 0; x2 – 4x + 4 = 0; (x – 2)2 = 0; x = 2.
Проверкой убеждаемся, что пара x = 2; y = 1 является решением второго уравнения системы.
Ответ: (2; 1).
3. 40 см;
MN =
= = 40 (см).
= 40 (см).
4. Найти градусную меру дуги MD.
MDK = 90°, так как опирается на диаметр.
MD =  = 2
= 2 .
.
tg MKD =  , то есть MKD = 30°, а значит, MD = 60°.
, то есть MKD = 30°, а значит, MD = 60°.
5. 9 ∙ (1 + 11 + ... + 1...1) = 9S;
(10 – 1) + (100 – 1) + ... = 9S;
9S = 10 + 102 + 103 + ... + 102000 – 2000;
9S = – 2000 = ;
S =  .
.
6. x1 3,8; y1 4,5; x2 –3,8; y2 –4,5;
x3 4,5; y3 2; x4 –4,5; y4 –2.
Вариант 4
1. Найти сумму натуральных чисел от 1 до 1000, которые делятся на 7 и не делятся на 13.
2. Решить систему уравнений:
3. Постройте график функции:
4. Дан выпуклый пятиугольник, все углы которого тупые. Доказать, что в нем найдутся две такие диагонали, что круги, построенные на них, как на диаметрах, полностью накроют пятиугольник.
5. Сколько одинаковых членов находится в двух арифметических прогрессиях 5; 8; 11... и 3; 7; 11... если в каждой из них по 100 членов?
6. По дороге мимо наблюдателя проехали через равные промежутки времени автобус, мотоцикл и автомобиль. Мимо другого наблюдателя они проехали с такими же промежутками времени, но в другом порядке: автобус, автомобиль и мотоцикл. Найти скорость автобуса, если скорость автомобиля 60 км/ч, а скорость мотоцикла 30 км/ч.
1. 66066.
2. Из первого уравнения следует | x | ≤ 1; | y | ≤ 1; | z | ≤ 1.
Отсюда x3 ≤ x2; y3 ≤ y2; z3 ≤ z2.
Если | x | y | z | x3 + y3 + z3 x2 + y2 + z2 = 1, но это неверно. Поэтому, если | x | = 1, то | y | = 0, | z | = 0. а из второго уравнения следует, что x = 1. Аналогично рассуждаем для | y | = 1 или | z | = 1.
Ответ: (1; 0; 0); (0; 1; 0); (0; 0; 1).
3. Графиком является прямая y = 3.
4. На диагоналях АС и AD построим круги, как на диаметрах с центрами O1 и O2. Они накроют ∆ABC и ∆AED, так как углы B и Е тупые. Если один из углов ACD и ADE тупой, то один из кругов с центром O1 и O2 покрывает ∆ACD. Если углы ACD и ADC не тупые, то круг с центром O1 покрывает ∆AHC, а круг с центром O2 покрывает ∆ADH. Значит, круги с центрами O1 и O2 полностью покрывают пятиугольник.
5. Пусть некоторые члены арифметических прогрессий равны:
5 + (n – 1) ∙ 3 = 3 + (m – 1) ∙ 4;
n = m +  – 1, m, n N, значит,
– 1, m, n N, значит,  = k, где k N, то есть
= k, где k N, то есть
m = 3k n = 4k – 1.
1 ≤ 4k – 1 ≤ 100;
2 ≤ 4k ≤ 101;
 ≤ k ≤ 25
≤ k ≤ 25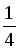 ;
;
k = 1, 2, ..., 25.
Ответ: общих членов 25 штук.
6. Пусть S – расстояние между наблюдателями, x – скорость автобуса, t – промежуток времени, через которое мимо первого наблюдателя последовательно проехали автобус, мотоцикл, автомобиль. Тогда время, затраченное автобусом, мотоциклом и автомобилем на пути от одного наблюдателя до другого, равно  ;
;  и
и  соответственно, а из условия задачи имеем
соответственно, а из условия задачи имеем  =
= + t;
+ t;  =
= – t.
– t.
Сложив их, получим , откуда x = 40. Значит, скорость автобуса равна 40 км/ч.
Вариант 5
1. Остаток при делении многочлена P (x) на (x – 1) равен 1, при делении P (x) на (x – 2) равен 2, а при делении P (x) на (x – 3) равен 3. Какой остаток будет при делении P (x) на (x – 1)(x – 2)(x – 3)?
2. Построить график | y | = y ∙  .
.
3. Войсковая колонна имеет длину 5 км. Связной, выехав из конца колонны, передал пакет в начало колонны и вернулся обратно. Колонна за это время прошла путь в 12 км. Какой путь проехал связной?
4. Решите в целых числах систему уравнений:
5. Найти площадь фигуры, заданной на координатной плоскости неравенством x2 + y2 ≤ 10 | x | + 4 | y |.
6. Найдите радиус окружности, описанной около правильного девятиугольника ABCDEFGHK, если известно, что площадь ∆ADG равна 48 .
.
1. P (x) = Q1 (x) ∙ (x – 1) + 1; Q1, Q2, Q3 – неполные частные;
P (x) = Q2 (x) ∙ (x – 2) + 2;
P (1) = 1; P (2) = 2; P (3) = 3;
P (x) = Q3 (x) ∙ (x – 3) + 3;
P (x) = Q (x) ∙ (x – 1)(x – 2)(x – 3) + ax2 + bx + c;
oткуда a = 1; b = –2; c = 1, то есть остаток x2 – 2x + 1.
2. Прежде всего надо отметить, что y ≥ 0.
При y 0 | cos x | = 1; cos x = ±1; x = πk; k Z.
При y = 0 x – любое, кроме x =  + πk; k Z, то есть график представляет собой совокупность прямых x = πk; k Z, параллельных оси ОY и оси ОХ с выколотыми точками x =
+ πk; k Z, то есть график представляет собой совокупность прямых x = πk; k Z, параллельных оси ОY и оси ОХ с выколотыми точками x =  + πk; k Z.
+ πk; k Z.
3. S = 5 км; x – скорость колонны, y – скорость связного.
;
;
5xy = 6y2 – 6x2;
6y2 – 5xy – 6x2 = 0;
D = 169x2;
y1 = 1,5x; y2
Откуда  ∙ y =
∙ y =  = 18 (км) проехал связной.
= 18 (км) проехал связной.
4.
Возможны варианты
Ответ: (x; y; z); (95; 0; 94); (31; 2; 32).
5. Достаточно рассмотреть случай для x ≥ 0; y ≥ 0, так как выражение симметрично относительно x, y:
x2 + y2 – 10x – 4y ≤ 0;
x2 – 10x + 25 + y2 – 4y + 4 – 29 ≤ 0;
(x – 5)2 + (y – 2)2 ≤ 29 – окружность с центром в точке (5; 2) и радиусом  . Sфигуры = 58π + 80.
. Sфигуры = 58π + 80.
6. AK = 40°; AKG = 120° ADG = 60;
∆ADG – равносторонний.
S = 48 ;
;
a = AD = 8 ;
;
AO = R – окружности, описанной около ∆ADG;
R =  = 8.
= 8.
Ответ: 8.
Вариант 6
1. Вычислить, не пользуясь таблицами и микрокалькулятором,
tg 1° ∙ tg 2° ∙ tg 3° ∙ ... ∙ tg 89°.
2. Решить уравнение: = 3x.
3. Найдите два трехзначных числа, сумма которых кратна 504, а частное кратно 6.
4. Непрерывная четная функция y = f (x) определена на всей числовой прямой. Для всех неотрицательных значений x значение f (x) совпадает со значением функции g (x) = x2 – 6x + 5. Найдите произведение корней уравнения f (x) = –3.
5. 30 стульев стоят в ряд. Время от времени к ряду подходит человек и садится на один из свободных стульев, при этом один из его соседей, если таковые есть, встает и уходит. Какое максимальное число стульев может быть занято, если в начале они все были пустыми?
6. Найти наименьшее значение параметра с, при котором система имеет одно решение.
1. tg 1° ∙ tg 2° ∙ tg 3° ∙ ... ∙ tg 87° ∙ tg 88° ∙ tg 89° =
= tg 1° ∙ tg 2° ∙ ... ∙ tg (90 – 2)° ∙ tg (90 – 1)° =
= tg 1° ∙ tg 2° ∙ ... ∙ ctg 2° ∙ ctg 1° = 1.
Использовать тождество tg ∙ ctg = 1.
2. Умножим обе части уравнения на сопряженное выражение:
; тогда получим
6x = 3x ∙ (), откуда с учетом того,
что x ≥ 0, получаем корни уравнения x1 = 0; x2 = 4.
3. Пусть a и b – искомые трехзначные числа, тогда
где f и k – целые числа, но так как числа a и b – трехзначные, то k = 1 – единственное значение, удовлетворяющее условию задачи.
Возможные значения f: 2, 3, 4, 5… 13 при f = 2; b = 144; a = 864, дальнейшие значения f рассматривать не имеет смысла.
Ответ: 144; 864.
4. g (x) = x2 – 6x + 5.
Корни уравнения x2 – 6x + 5 = –3: x1 = 4; x2 = 2, учитывая четность
функции y = f (x), корни уравнения f (x) = –3: x1 = 4; x2 = 2; x3 = –4;
x4 = –2, то есть произведение корней x1 ∙ x2 ∙ x3 ∙ x4 = 4 ∙ 2 ∙ (–4) ∙ (–2) = 64.
Возможен графический способ решения.
5. 15 стульев.
6. c =  .
.
Вариант 7
1. Найдите значение выражения , если
= 3.
2. Постройте график функции y = 4 sin x ∙ | cos x |.
3. Сумма третьего и четырнадцатого членов арифметической прогрессии равна наибольшему значению трехчлена –2x2 + 4x – 16. Найдите сумму шестнадцати первых членов этой прогрессии.
4. Составьте формулу, с помощью которой выражался бы n-й член последовательности вида 0; 2; 2; 4; 4; 6; 6; ...
5. В сосуде имеется три крана. Через первый и второй краны вода вливается, через третий выливается. Один первый кран может наполнить сосуд за 10 часов, а один второй – за 15 часов. При совместном действии всех трех кранов из полного сосуда выливается вся вода за 30 часов. Сосуд был полон, когда открыли первый и третий краны. Через 1 час после их открытия первый кран был закрыт, но открыт второй, а еще через 1 час закрыли третий кран и вновь открыли первый.
Определите, через сколько часов после закрытия третьего крана два первых наполнят сосуд.
6. Разность катетов прямоугольного треугольника равна биссектрисе прямого угла. Вычислите отношение этих катетов.
1. x2 + y (x + 7y) = 3 (xy + 2y2), откуда (x – y)2 = 0, то есть x = y. Тогда = –3.
2. y = 4sin x ∙ | cos x | =
3. S16 = –112.
4. an = n +  .
.
5. 6 часов.
6. Пусть катеты прямоугольного ∆ABC равны a и b. Через вершину В проведем прямую, параллельную биссектрисе СЕ и пересекающую продолжение катета АС в точке D.
∆ABD и ∆ACE подобны, значит, , или CE =  , но по условию
, но по условию  = b – a (b a), отсюда находим b2 – ab
= b – a (b a), отсюда находим b2 – ab – a2 = 0; , но
– a2 = 0; , но  0, поэтому .
0, поэтому .
Вариант 8
1. Найти в градусах угол , под которым окружность x2 + y2 = 32 видна из точки А (8; 0).
2. Сто человек ответили на вопрос: «Будет ли новый президент лучше прежнего?» Из них a человек считают, что будет лучше, b – что будет такой же и c – что будет хуже. Других ответов не было. Социологи построили два показателя «оптимизма» опрошенных: m = a +  ; n = a – c. Оказалось, что m = 40. Чему в таком случае равно n?
; n = a – c. Оказалось, что m = 40. Чему в таком случае равно n?
3. Через точку М на диаметре окружности проводится секущая CD под углом 45° к диаметру. Докажите, что число | CM | 2 + | DM | 2 не зависит от положения точки М на диаметре.
4. Решить неравенство: ≥ 0.
5. Решить уравнение: 3 ∙ cos x – cos 3x = 2 (x2 + ) + π ∙ .
) + π ∙ .
6. Возраст одного человека в 1990 году был равен произведению цифр года его рождения. В каком году он родился, если известно, что ему меньше 90 лет?
1. 90°.
2. Учитывая, что c = 100 – a – b, получаем:
n = a – (100 – a – b) = 2a + b – 100 = 2– 100 = 2m – 100.
значит, n = 2 ∙ 40 – 100 = –20.
3. Для доказательства: постройте точку D′, симметричную точке D относительно диаметра.
4. (2; 4) {0} {6}.
5. Использовать метод оценки для функций
f (x) = 3cos x – cos 3x; g (x) = 2 ∙ (x2 +  ) + π.
) + π.
наибольшее значение функции f равно наименьшему значению функции g (x) в двух точках: x1 =  ; x2 =
; x2 =  . можно использовать графическую иллюстрацию решения.
. можно использовать графическую иллюстрацию решения.
6. 1918 год.
Вариант 9
1. Дан угол в 19°. Построить с помощью циркуля и линейки угол в 1°.
2. Найдите три числа, если куб первого числа на 2 больше их произведения. Куб второго числа на 3 меньше их произведения, а куб третьего числа на 3 больше их произведения.
3. Решить неравенство: .
4. Четырехугольник АВСD вписан в окружность. Продолжение стороны AB за точку B пересекается с продолжением стороны CD в точке E.
Найти угол ADE, если CD = 2EB; AB : EC = 7 : 2, косинус угла AED равен  .
.
5. Доказать тождество: 2 (sin6 x + cos6 x) – 3 (sin4 x + cos4 x) + 1 = 0.
6. При каких значениях параметра а уравнение | x2 – 5x + 4 | = ax имеет ровно три корня?
1. Необходимо воспользоваться тем, что 19° ∙ 19 = 361°.
2. Пусть x, y, z – данные числа, тогда
(xyz)3 = (xyz + 2) ∙ (xyz – 3) ∙ (xyz + 3).
Пусть xyz = t;
t3 = (t + 2) ∙ (t – 3) ∙ (t + 3) 2t2 – 9t – 18 = 0. t1 = 6; t2 =  , значит, xyz = 6 или xyz =
, значит, xyz = 6 или xyz =  , откуда необходимо рассмотреть решение двух систем уравнений:
, откуда необходимо рассмотреть решение двух систем уравнений:
x1 = 2; y1 =  ; z1 =
; z1 =  ;
;
x2 =  ; y2 = –
; y2 = – ; z2 =
; z2 =  .
.
3. (–∞; –2) (0; 10) (18; +∞).
4. По свойству секущей и касательной имеем BE ∙ (AB + BE) =
= EC ∙ (DC + EC). Пусть BE = x, AB = 7y, DC = 2x, EC = 2y; подставляя в предыдущее равенство, получим, что x = y.
Из ∆BCE по теореме косинусов BC =  ; ADE = CBE, поэтому из ∆BEC CBE = π – arccos
; ADE = CBE, поэтому из ∆BEC CBE = π – arccos ; ADE = CBE.
; ADE = CBE.
5. 2 (sin2x + cos2x) ∙ (sin4x – sin2x cos2x + cos4x) – 3 (sin4x + cos4x) + 1 =
= –sin4x – 2sin2x cos2x – cos4x + 1 = –(sin2x + cos2x)2 + 1 = 0.
6. При a = 1 можно использовать графическую иллюстрацию аналитического решения.
Вариант 10
1. Найти значение выражения x3 – 3x при x =  .
.
2. Найти все решения уравнения , удовлетворяющие условию ctg x
3. Вычислить arccos (cos 10).
4. Составить уравнение окружности наименьшего радиуса, внутри которой помещается множество точек, заданной на координатной плоскости условием: | 3x – y – 1 | + | 3x – 6 |
5. Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие – на хорде. Чему равна разность сторон этих квадратов?
6. В компании из шести человек один правдолюб, то есть всегда говорит правду; двое – дипломаты, то есть могут говорить правду или ложь; а остальные – лжецы, то есть всегда лгут. Чтобы узнать, кто из них есть кто, каждого спросили, кто он есть. Первый сказал, что правдолюб, второй – что он дипломат, третий – что он лжец, четвертый – что он не правдолюб, пятый – что он не дипломат, а шестой – что он не лжец.
Кто из них есть кто?
Вариант 10
1. Найти значение выражения x3 – 3x при x =  .
.
2. Найти все решения уравнения , удовлетворяющие условию ctg x
3. Вычислить arccos (cos 10).
4. Составить уравнение окружности наименьшего радиуса, внутри которой помещается множество точек, заданной на координатной плоскости условием: | 3x – y – 1 | + | 3x – 6 |
5. Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие – на хорде. Чему равна разность сторон этих квадратов?
6. В компании из шести человек один правдолюб, то есть всегда говорит правду; двое – дипломаты, то есть могут говорить правду или ложь; а остальные – лжецы, то есть всегда лгут. Чтобы узнать, кто из них есть кто, каждого спросили, кто он есть. Первый сказал, что правдолюб, второй – что он дипломат, третий – что он лжец, четвертый – что он не правдолюб, пятый – что он не дипломат, а шестой – что он не лжец.
Кто из них есть кто?
1. 2 .
.
2. ;
(2 ∙ (3 +  ) + 1 – 2
) + 1 – 2 )2sin x = 7–1;
)2sin x = 7–1;
72sin x = 7–1;
sin x = 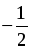 , с учетом условия ctg x x =
, с учетом условия ctg x x =  + 2πk, k Z.
+ 2πk, k Z.
3. arccos (cos 10) = arccos (cos (4π – 10)) = 4π – 10, так как
(4π – 10) [0; π].
4. Рассмотрим четыре случая:
1) 3)
2) 4)
Множество точек, заданных полученными условиями, представляют собой параллелограмм ABCD, O – точка пересечения диагоналей. AC – большая диагональ, OC = R – радиус: (x – 2)2 + (y – 5)2 =  (необходима графическая иллюстрация решения).
(необходима графическая иллюстрация решения).
5. 1,6h.
6. Первый, второй, шестой – лжецы; третий, четвертый – дипломаты; пятый – правдолюб.







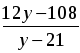 ; y = 9; x = 0.
; y = 9; x = 0.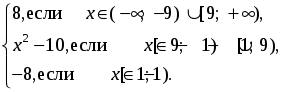

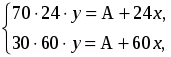
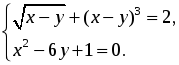
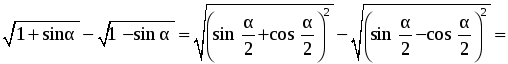
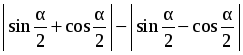 = sin
= sin 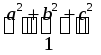 + 2ab + 2bc + 2ac = 0;
+ 2ab + 2bc + 2ac = 0;









