Практическое занятие Приложение 29
Основные приемы решения уравнений.
Корни уравнений. Равносильность уравнений. Преобразование уравнений.
1) Теоретический этап. Опорный конспект.
Уравнением с одной переменной x называется выражение f(x) = g(x), содержащее переменную величину x и знак равенства.
Число a называется корнем уравнения f(x) = g(x), если при подстановке этого числа в уравнение получается верное числовое равенство.
Решение уравнения – это процесс, состоящий в основном в замене заданного уравнения другим уравнением, ему равносильным. Такая замена называется тождественным преобразованием.
Основные тождественные преобразования:
Замена одного выражения другим, тождественно равным ему.
Например, уравнение (3x+ 2) 2 = 15x+10 можно заменить следующим равносильным:
9x2 + 12x +4 = 15x + 10
Перенос членов уравнения из одной стороны в другую с обратными знаками.
Так, в предыдущем уравнении мы можем перенести все его члены из правой части в левую со знаком « – »: 9x2 + 12x + 4 – 15x – 10 = 0, после чего получим: 9x2 – 3x – 6 = 0 .
Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля. Уравнение x – 1 = 0 имеет единственный корень x = 1. Умножив обе его части на x – 3 , мы получим уравнение (x – 1)(x – 3 ) = 0, у которого два корня: x = 1 и x = 3. Последнее значение не является корнем заданного уравнения x – 1 = 0. Это так называемый посторонний корень. И наоборот, деление может привести к потере корня. Так, если (x – 1)(x – 3) = 0 является исходным уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x – 3 .
Можно возвести обе части уравнения в нечетную степень или извлечь из обеих частей уравнения корень нечетной степени. Необходимо помнить, что: а) возведение в четную степень может привести к приобретению посторонних корней;
б) неправильное извлечение корня четной степени может привести к потере корней.
Уравнение 7x = 35 имеет единственный корень x = 5. Возведя обе части этого уравнения в квадрат, получим уравнение: 49x2 = 1225 , имеющее два корня: x = 5 и x = – 5. Последнее значение является посторонним корнем.
Неправильное извлечение квадратного корня из обеих частей уравнения 49x 2 = 1225 даёт в результате 7x = 35,и мы теряем корень x = – 5. Правильное извлечение квадратного корня приводит к уравнению: | 7x | = 35, следовательно, к двум случаям: 1) 7x = 35,
тогда x = 5; 2) – 7x = 35, тогда x = – 5. Следовательно, при правильном извлечении квадратного корня мы не теряем корней уравнения.
Решение уравнений
Показательные уравнения.
1) Если показательное уравнение сводится к виду ax = ab (1) где a 0 и a ≠1, то оно имеет единственный корень х = b.
2) Иногда, чтобы привести показательное уравнение к виду (1), необходимо в левой части уравнения вынести за скобки общий множитель а х, например:
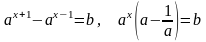
3) Некоторые показательные уравнения заменой а х = t сводятся к квадратным.
Надо помнить, что t 0, так как показательная функция не может принимать отрицательные значения.
Логарифмические уравнения.
Чаще всего при решении логарифмического уравнения его приводят к виду
loga (f(x)) = log a (g(x)), тогда f(x) = g(x).
Решив полученное уравнение, следует сделать проверку корней, чтобы исходное уравнение не потеряло смысл.
2) Подготовительный этап. Перепишите и заполните пропуски:
Пример 1. Решить уравнение: 9 х – 7 3 х = - 12
3 х = - 12
Решение:
9 х – 7 3 х = - 12; Пусть 3 х = t , t 0; t2 - 7t + 12=0; D = 1; t1 = 3, t 2= 4.
3 х = - 12; Пусть 3 х = t , t 0; t2 - 7t + 12=0; D = 1; t1 = 3, t 2= 4.
Делаем обратную замену 1) 3x = 3; 2) 3x = 4
x1 = …; x 2 = 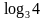
Ответ: х1 = 1; x 2 = 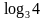 .
.
Пример 2. Решить уравнение: 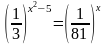
Решение: 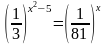 . Уравниваем основания :
. Уравниваем основания :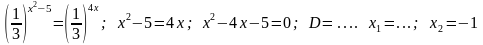 .
.
Ответ: x1= 5; x2 = - 1
Пример 3. Решить уравнение: log5 (x2 - 10) = log 5 9x
Решение: log5 (x2 - 10) = log 5 9x; x2 - 9x – 10 = 0, D = …; x1=10, x2= -1
Проверка: при х = 10, log5 (102 - 10) = log 5 (9 ∙10) – верно
Ответ: x = 10
Пример 4. Решить уравнение: log 7 (x2 + 6x) = 1;
Решение: log 7 (x2 + 6x) = 1;
x2 + 6x =71 ; x2 + 6x – 7 = 0; D = 64; x1 = - 7 u x2 = …
Проверка: при х = - 7, log 7 ((- 7)2 + 6 ∙(-7)) = 1 – верно
при х = 1, log 7 (12 + 6 ∙1) = 1 – верно
Ответ. x1= - 7; x 2= 1.
Пример 5. Решить уравнение log2 (x – 5) + log2 (x +2) = 3
Решение: log2 (x – 5) + log2 (x +2) = 3
Используем свойство логарифмов: log2(( x-5)(x + 2)) = 3; (x-5)(x+2) = 23; (x-5)(x+2) = 8;
х2 + …х – 5х – 10 = 8; x2 – 3x - 18 = 0; D = …; x1 = – 3; x2 = ….
Проверка: при x = – 3, log2 (– 3 – 5) + log2 (– 3 +2) = 3 – неверно
При х = 6, log2 (6 – 5) + log2 (6 + 2) = 3 – верно
Ответ: х = 6.
Пример 6. Решить уравнение: 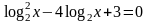 .
.
Решение: 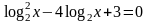
Пусть 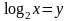 , тогда у2 – 4у + 3 = 0; D = …; у1 = 1; у2 = …
, тогда у2 – 4у + 3 = 0; D = …; у1 = 1; у2 = …
Сделаем обратную подстановку:
1) 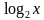 = 1; х = 2; 2)
= 1; х = 2; 2) 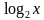 = 3; х = 23 ; х = …
= 3; х = 23 ; х = …
Ответ: х = 2, х = 8.
3) Практический этап.
1. Решить уравнение: 4х – 6 ∙ 2х = – 8
2. Решить уравнение: 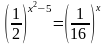
3. Решить уравнение: log3 (x2 + 6) = log3 5x
4. Решить уравнение: log12 (x2 – x) = 1
5. Решить уравнение: 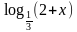 +
+ 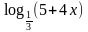 = 0
= 0
6. Решить уравнение: log22 Х – 4 log 2 Х = 12
4) Дополнительные задания*
1. Укажите промежуток, которому принадлежит корень уравнения: 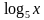 +
+ 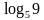 = 3
= 3
1) [ – 10; – 15] ; 2) (5; 10); 3) (10; 13); 4) [ 10; 15]
2. Укажите промежуток, которому принадлежит корень уравнения: 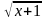 х = 1
х = 1
1) [ 2; 5] ; 2) (– 2; – 1); 3) [– 1; 1]; 4) [ 1; 2]
3. Найдите сумму корней уравнения: ( 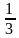 )2х + 5∙ (
)2х + 5∙ ( 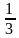 )х – 24 = 0
)х – 24 = 0
4.Укажите промежуток, которому принадлежит корень уравнения: log 5 (3х – 1) = 3
1) (15; 20) ; 2) [ 0; 2]; 3) (20; 40); 4) [ 40; 50]
5. Найдите сумму корней уравнения: 3 2х – 4 3х + 3 = 0
3х + 3 = 0
6. Решите уравнение lg(5х + 11) – lg( 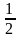 ) = lg13
) = lg13
7. Решите уравнение: 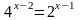







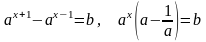
 3 х = - 12
3 х = - 12 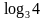
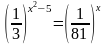
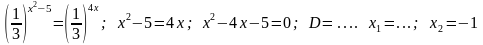 .
.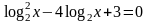 .
.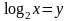 , тогда у2 – 4у + 3 = 0; D = …; у1 = 1; у2 = …
, тогда у2 – 4у + 3 = 0; D = …; у1 = 1; у2 = …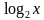 = 1; х = 2; 2)
= 1; х = 2; 2) 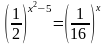
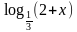 +
+ 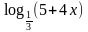 = 0
= 0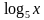 +
+ 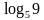 = 3
= 3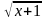 х = 1
х = 1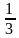 )2х + 5∙ (
)2х + 5∙ ( 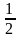 ) = lg13
) = lg13