Конспект урока геометрии в 7 классе по теме «Неравенство треугольника»
Предмет (направленность): геометрия
Класс: 7
Место проведения: МАОУ «ДСОШ №1»
Цели урока:
- доказать теорему о неравенстве треугольника;
- показать применение теоремы о неравенстве треугольника при решении практических заданий.
Задачи:
- повторить знания о соотношениях между сторонами и углами треугольника;
- познакомить с понятием «неравенство треугольника»;
- усвоить теорему о неравенстве треугольника;
- формировать умение применять теорему о неравенстве треугольника при решении задач;
- формировать навык формулировать, аргументировать и отстаивать своё мнение;
- формировать навык работы по алгоритму;
- формировать навык самооценки;
- развивать вычислительные навыки;
- развивать предметную речь;
- повышать любознательность детей, стремление к использованию приобретенного на уроке опыта деятельности в реальной жизни, за рамками учебного процесса.
Планируемые предметные и метапредметные результаты обучения:
Научатся:
- доказывать теорему о неравенстве треугольника;
- применять теорему о неравенстве треугольника;
- работать по алгоритму;
- работать в группе;
- объяснять выполненные действия;
- формулировать выводы и умозаключения.
Получат возможность научиться:
- применять математические знания в решении задач по геометрии.
Оборудование:
- презентация
- проектор;
- палочки разной длины;
- оценочный лист;
- опорный конспект;
- треугольники из цветной бумаги на каждую парту (для рефлексии).
- набор по геометрии
Этапы урока
| 1. | Организационный момент. Мотивация к учебной деятельности. | 2 минуты |
| 2. | Актуализация опорных знаний. | 6 минут |
| 3. | Творческое применение и добывание знаний в новой ситуации (проблемное задание). | 7 минут |
| 4. | Усвоение новых знаний. | 6 минут |
| 5. | Физминутка | 2 минуты |
| 6. | Закрепление. Самостоятельная работа с самоконтролем. | 6 минут |
| 7. | Подведение итогов урока. Рефлексия учебной деятельности. | 4 минуты |
| 8. | Информация о домашнем задании | 2 минуты |
Ход урока
Организационный момент. Мотивация к учебной деятельности.
Здравствуйте, уважаемые ребята. Меня зовут Марина Николаевна, я рада вас приветствовать на нашем уроке геометрии. Сегодня у нас на уроке присутствуют гости, давайте их поприветствуем.
У вас на столах лежат рабочие и оценочные листы, которые мы будем заполнять во время урока.
Свой урок хочу я начать с высказывания древнегреческого философа Платона (Слайд 1).
Как вы понимаете данное высказывание? Ответы детей.
Итог. Если в биологии все живые организмы состоят из клеток, так и геометрия состоит из треугольников.
Наверное, вы догадались, о чём речь пойдёт на уроке?
Правильно, треугольник. А что это за фигура? Дети дают определение треугольника.
Молодцы !
Актуализация опорных знаний.
Треугольник – это «Королевская» фигура в геометрии. Мы очень часто встречаемся с треугольниками при решении задач и постоянно узнаём о них что-нибудь новое. Казалось бы, больше уже ничего нового о треугольнике узнать невозможно, однако это заблуждение. И сегодня мы в этом убедимся. Но для этого нам необходимо подготовиться к «открытию нового знания» и поможет в этом нам игра «ДаНетка».
Один ученик будет работать у закрытой доски, остальные работают в рабочих листах.
Игра «ДаНетка».
1.Все высоты равностороннего треугольника равны.
2.Против большего угла лежит меньшая сторона.
3.Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
4.В равнобедренном треугольнике углы при основании равны.
5.Против меньшей стороны лежит меньший угол.
6.В тупоугольном треугольнике все углы тупые.
7.Против большего угла лежит большая сторона.
8.Треугольник называется равнобедренным, если равны две его стороны.
Взаимопроверка. Обменяйтесь листами с соседом по парте. Ответы: да, нет, нет, да, да, нет, да, да, с пояснением учеников.
Посчитайте количество верных ответов.
Выставим в оценочный лист себе результаты. Если 7-8 правильных ответов, то себе ставим «5», если 5-6 правильных- оценка «4», если меньше 5 баллов-не расстраивайся, у тебя все получится!
Творческое применение и добывание знаний в новой ситуации (проблемное задание).
Скажите, а где еще в повседневной жизни вам встречались треугольные формы? В архитектуре? (Знак аварийной остановки и т.д. Крыши имеют треугольную форму.)
– Вы правы. Основу крыш составляют наклонные и горизонтальные балки, которые соединены между собой и образуют треугольник.
Сегодня наш класс – это проектный институт. Ряды – это отделы. Получается - три отдела. Вы – инженеры проектировщики. А я - ваш начальник.
Итак. В наше проектное подразделение поступил заказ от застройщика: спроектировать в парк отдыха крышу для беседки треугольной формы. Заказчик направил нам условия (три варианта). Ваша задача – выполнить требуемые расчеты. Каждому отделу я раздам один из вариантов условия (задания раздаются по рядам).
Задания:
Отдел 1 (1 ряд).1 сторона -150, вторая-300, третья-300
Отдел 2 (2 ряд). 1 сторона -150, вторая – 200, третья -350
Отдел 3 (3 ряд). 1 сторона- 100, вторая 150, третья- 300
Давайте теперь попробуем сделать макет этой крыши. Каждому отделу я раздала палочки разной длины. Вам надо в соответствии с вашими расчетами и масштабом, представленном на слайде (1:10)нужно собрать , чтобы получился треугольник. Работаем в группах.
Прошу руководителей отделов показать результаты. Что у вас получилось?
Руководители отделов показывают макеты крыш и делают вывод, что не всегда возможен треугольник.
А как вы думаете, почему?
Ответы учащихся.
Для того, чтобы построить треугольник должны выполнятся определенные условия. Какие? Дети затрудняются ответить.
Предлагаю одному представителю из отдела выйти к доске и сравнить каждую сторону треугольника с суммой двух других сторон.
Треугольник получился там, где сторона треугольника не должна быть больше или равна сумме двух других сторон.
Смотрите во втором отделе есть сторона треугольника, которая равна сумме двух других сторон, а в третьем отделе есть сторона, которая больше суммы других сторон. А такого быть не должно, иначе треугольник не получится.
Кто сможет сделать соответствующую запись на доске, обозначив стороны треугольника через а, в и с?
К доске выходит желающий ученик и собирает неравенство а
Значит сегодня мы будем говорить, о чем? Неравенство треугольника. Это тема нашего урока. Давайте оценим себя за проектную работу.
Усвоение новых знаний.
Итак, тема нашего урока «Неравенство треугольника»
Теорема: Каждая сторона треугольника меньше суммы двух других сторон.
Как проверить правильность любого высказывания или утверждения? Доказать!
Н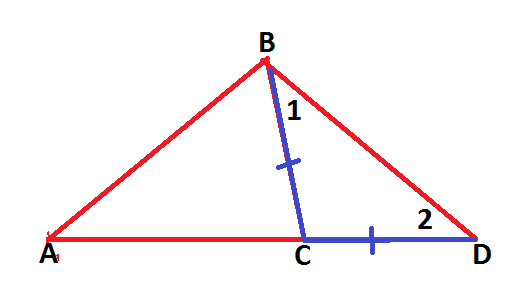 а столах у вас лежат опорные конспекты, давайте заполним их.
а столах у вас лежат опорные конспекты, давайте заполним их.
Дано: ∆АВС
Доказать: АВ
Доказательство:
Рассмотрим произвольный треугольник ABC.
Отложим на продолжении стороны AC отрезок CD, равный стороне CB.
В равнобедренном треугольнике BCD 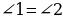 , а в треугольнике ABD
, а в треугольнике ABD 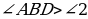 .
.
Так как в треугольнике против большего угла лежит большая сторона, то AB AD.
Но AD=AC+CD=AC+CB, поэтому AB
Что требовалось доказать.
Как вы думаете, для каждой ли стороны надо проверять неравенства треугольника?
Ответы учащихся.
Оказывается, достаточно проверить выполнение неравенства для большей стороны. Как вы думаете, почему?
Ответы учащихся. Запас.
Данная теорема и ее доказательство встречается и в региональном зачете по геометрии в билете № 13 в вопросе №2
Давайте сделаем перерыв и немного отдохнем. Физминутка на слайде.
Закрепление.
Далее поработаем с учебником. Откройте страницу 75, номер 253 устно, 255(а).
Самостоятельная работа с самоконтролем (пликерс)
А теперь проверяем результаты и выставляем себе оценку. Все задания выполнены правильно, поставьте себе «5», если 2 задания –«4», если 1 задание -не переживай, у тебя все получится!
Подведение итогов урока. Рефлексия учебной деятельности.
Давайте еще раз проговорим условие для построения треугольника.
Ученики проговаривают теорему о неравенстве треугольника: каждая сторона треугольника меньше сумму двух других сторон.
Рефлексия:
На партах лежат заранее приготовленные (вырезанные из цветной бумаги) треугольники.
Если урок был интересен, на уроке вы работали и в итоге поняли материал, то поднимите красный треугольник.
Если тема урока вызвала трудность и вам эту тему нужно еще закрепить, то поднимите синий треугольник.
Если урок был не интересным, и вы ничего не поняли, то поднимите зеленый треугольник. Вы заметили, что у нас стоит елочка, но какая то она неинтересная, давайте мы украсим ее своими выбранными треугольниками.
Информация о домашнем задании.
На следующем уроке мы будем учиться применять теорему «Неравенство треугольника» в задачах. Для этого вам надо:
Выучить теорему о неравенстве треугольника (с доказательством).
Выполнить № 255 (б, в),
257 за доп. оценку







 а столах у вас лежат опорные конспекты, давайте заполним их.
а столах у вас лежат опорные конспекты, давайте заполним их.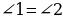 , а в треугольнике ABD
, а в треугольнике ABD 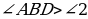 .
.









