Параллельное проектирование

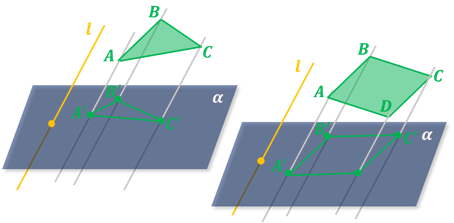
Тема:  Параллельное проектирование.

Прочитать:

В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры.

Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.

Пусть    — некоторая плоскость,

         — некоторая прямая, пересекающая эту плоскость.

Возьмём в пространстве произвольную точку   .

Если точка    не лежит на прямой   , то проведём через точку    прямую, параллельную прямой   , и обозначим через    точку пересечения этой прямой с плоскостью   .

Если же точка    лежит на прямой   , то обозначим через    точку пересечения прямой    с плоскостью   .

Записать:

Точка    называется проекцией точки    на плоскость    при проектировании параллельно прямой    (или параллельной проекцией точки   ).

Плоскость    называется плоскостью проекций, а о прямой    говорят, что она задаёт направление проектирования.

Все прямые, параллельные прямой   , задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми.

Прочитать:

Примеры параллельных проекций дают, например, тени предметов под воздействием пучка параллельных солнечных лучей.

Пусть    — плоская или пространственная фигура. Проекцией фигуры    на плоскость    при проектировании параллельно прямой    называется множество    проекций всех точек фигуры   .

Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.

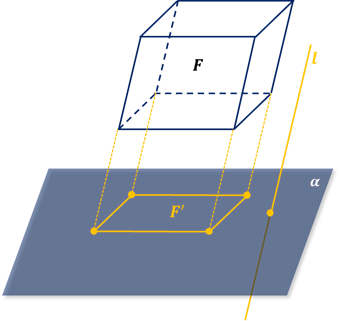
Свойства параллельного проектирования

Вспомним основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.

 1. Проекция прямой есть прямая, а проекция отрезка — отрезок.

2. Проекции параллельных прямых параллельны или совпадают.

3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.

Следствие.

- При параллельном проектировании середина отрезка проектируется в середину его проекции.

- При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых.

- Если точка делит отрезок в отношении   , то проекция точки будет делить проекцию отрезка также в отношении   .

- Центр правильного треугольника отображается в точку пересечения медиан проекции этого треугольника, центр квадрата — в точку пересечения диагоналей проекции квадрата.