Перпендикулярность плоскостей: признак перпендикулярности двух плоскостей

Перпендикулярность плоскостей: признак перпендикулярности двух плоскостей.

Повторим!

Двугранным углом называется фигура, образованная прямой  а  и двумя полуплоскостями с общей границей в виде прямой  а , не принадлежащими одной плоскости. Полуплоскости , образующие двугранный угол, называются его гранями . Прямая  а , которая является общей границей полуплоскостей, называется ребром двугранного угла

Повторим!

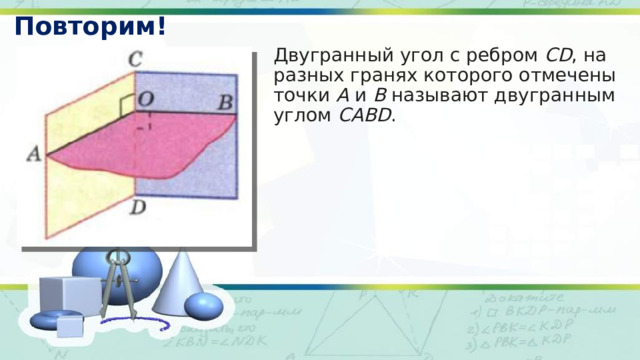
Двугранный угол с ребром  CD , на разных гранях которого отмечены точки  A  и  B  называют двугранным углом  CABD .

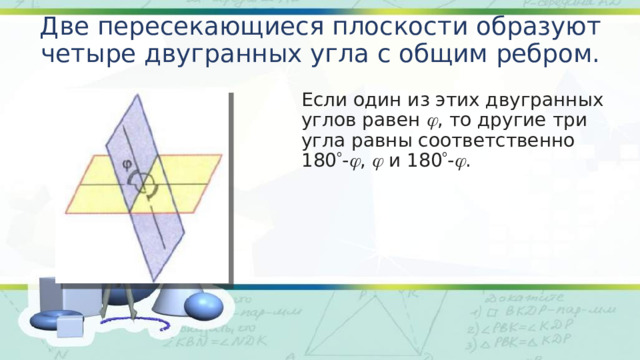
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

Если один из этих двугранных углов равен   , то другие три угла равны соответственно 180  -  ,    и 180  -  .

Определение перпендикулярных плоскостей

В частности, если один из углов прямой, то и остальные три угла прямые. Если угол между пересекающимися плоскостями равен 90 градусом, будем называть такие плоскости перпендикулярными.

Признак перпендикулярности плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то эти плоскости перпендикулярны.

Рассмотрим плоскости    и    такие, что плоскость    проходит через прямую  АВ , АВ     и АВ    = А . Докажем, что          .

           = АС . При этом прямая  АВ      АС , так как по условию прямая  АВ      , это означает, что прямая  АВ  перпендикулярна к любой прямой, лежащей в плоскости    .

Проведем в плоскости     прямую  AD , перпендикулярную к прямой  АС . Тогда    BAD  — линейный угол двугранного угла, образованного при пересечении плоскостей     и    . Но  BAD = 90  , так как   АВ      . Следовательно, угол между плоскостями     и     равен 90  .

Что и требовалось доказать.

Следствие

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Если  = a,   a, то    и   

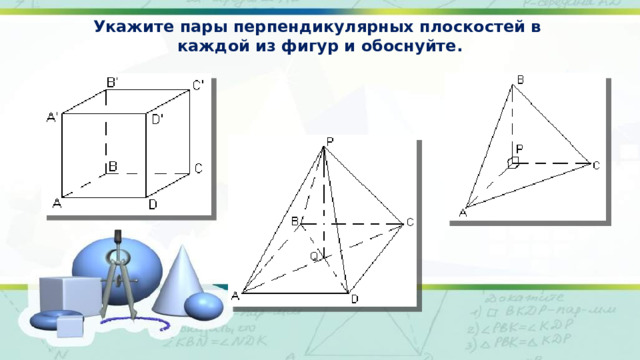
Укажите пары перпендикулярных плоскостей в

каждой из фигур и обоснуйте.

Задача № 1

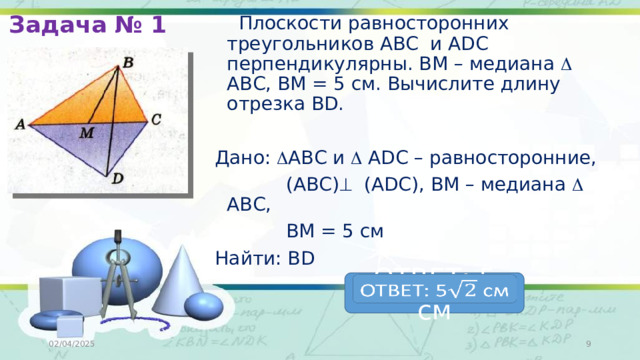
Плоскости равносторонних треугольников АВС и ADC перпендикулярны. ВМ – медиана  АВС, ВМ = 5 см. Вычислите длину отрезка ВD.

Дано:  АВС и  ADC – равносторонние,

(АВС)  (ADC), ВМ – медиана  АВС,

ВМ = 5 см

Найти: ВD

ОТВЕТ: 5 см

02/04/2025

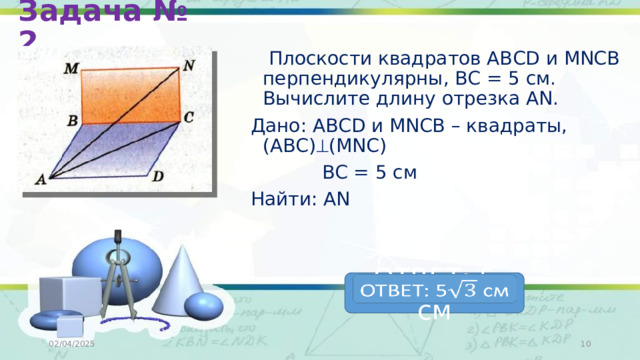
Задача № 2

Плоскости квадратов АВСD и MNCB перпендикулярны, ВС = 5 см. Вычислите длину отрезка АN.

Дано: АВСD и MNCB – квадраты, (АВС)  (MNC)

ВС = 5 см

Найти: АN

ОТВЕТ: 5 см

02/04/2025

Задача № 3

Плоскости прямоугольного треугольника АВС (  С = 90  ) и квадрата ACPR перпендикулярны. Сторона квадрата 6 см, гипотенуза АВ = 10 см. Найдите длину отрезка ВP.

Дано:  АВС – прямоугольный, ACPR – квадрат,

(АВС)  (ACP), АС = 6 см, АВ = 10 см

Найти: ВР

ОТВЕТ: 10 см

02/04/2025

Задача № 4

Отрезок МК перпендикулярен плоскости прямоугольного треугольника АВС (  С = 90  ). KN  AC, AK = KB, AC = 12 см, MK = 8 см. Найдите длину отрезка MN.

Дано:  АВС – прямоугольный, МК  (АВС), KN  AC,

AK = KB, AC = 12см, MK = 8 см.

Найти: MN

ОТВЕТ: 10 см

02/04/2025

Задача № 5

Плоскости равнобедренных треугольников АВС и АDС перпендикулярны. АС – их общее основание. ВК – медиана  АВС, ВК = 8 см, DК = 15 см. Найдите длину отрезка ВD.

Дано:  АВС и  АDС – равнобедренные,

АС – общее основание, (АВС)  (АDС),

ВК – медиана  АВС, ВК = 8 см, DК = 15 см.

Найти: ВD

ОТВЕТ: 17 см

02/04/2025

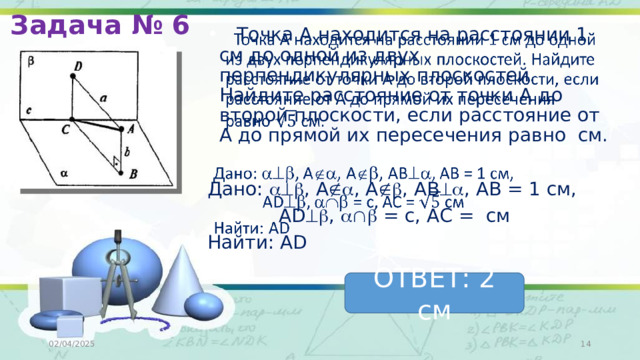
Задача № 6

Точка A находится на расстоянии 1 см до одной из двух перпендикулярных плоскостей. Найдите расстояние от точки A до второй плоскости, если расстояние от A до прямой их пересечения равно см.

Дано:  , А  , А  , АВ  , АВ = 1 см,

АD  ,  = с, АС = см

Найти: АD

ОТВЕТ: 2 см

02/04/2025

Задача № 7

Отрезок длиной 25 см опирается концами на две перпендикулярные плоскости. Расстояние от концов отрезка до плоскостей равны 7 см и 15 см. вычислите проекции отрезка на каждую из плоскостей.

Дано:  , АВ  = В, АВ  =А, АВ = 25 см,

АС  , BD  , АС = 7 см, BD = 15 cм

Найти: ВС, АD

ОТВЕТ: 24 см, 20 см

02/04/2025

Домашнее задание

Выучить правила § 23 стр. 49 учить

Выполнить в тетради:

1. Отрезок длиной 25 см опирается концами на две взаимно перпендикулярные плоскости. Проекции отрезка на эти плоскости равны и 20 см. Найдите расстояния от концов отрезка до данных плоскостей.