Просмотр содержимого документа
«ОЦЕНОЧНЫЙ ЛИСТ»
Просмотр содержимого документа
«Рейтинговая самостоятельная работа»
Просмотр содержимого документа
«самостоятельная работа»
Просмотр содержимого документа
«тех карта урока геометрии»
Технологическая карта урока
Предмет: геометрия класс: 8 учебник и УМК Л.С.Атанасяна
Учитель: Капустянская Е.В.
Тема урока: «Пересечение высот треугольника».
Оборудование: интерактивная доска, раздаточный материал.
Цели и задачи урока:
Предметные: расширить знания учащихся о треугольниках; практическим путем выяснить где пересекаются высоты треугольника (или их продолжения), доказать теорему о пересечении высот треугольника, научить решать задачи на применение нового материала.
Метапредметные:
РУУД – развивать навыки самоорганизации, умение определить цель предстоящей познавательной деятельности, её вид, уровень сложности, пути достижения ожидаемого результата; развивать умение контролировать и оценивать свои действия.
ПУУД – создавать условия для развития навыков самостоятельной познавательной деятельности; для развития навыков владения устной речью, способностью формулировать собственное мнение и аргументировать его, развивать логическое мышление, умение устанавливать причинно-следственные связи.
КУУД – способствовать развитию навыков организации учебного сотрудничества с учителем и одноклассниками, умений работать в паре, согласовывать свои действия, оказывать необходимую взаимопомощь друг другу.
Личностные – создавать условия для развития самосознания, самоопределения, смыслообразования, позитивной оценки происходящих событий.
Ход урока
| Основные этапы организации учебной деятельности | Цель этапа | Содержание педагогического взаимодействия
|
| Деятельность учителя | Деятельность обучающихся
|
|
|
|
|
| Познаватель-ная | Коммуника-тивная | Регулятивная |
| 1. организационный 2 мин. | Мотивирование обучающихся на предстоящую деятельность. | Оказание помощи обучающимся в постановке цели предстоящей деятельности и прогнозировании её результатов.
| Изучают оценочные листы | Слушают учителя. | Постановка цели; прогнозирование результата. |
|
| Учитель приветствует учащихся, проверяет их готовность к уроку. -Для повышения мотивационной заинтересованности на уроке будут использованы индивидуальные оценочные листы. -Посмотрите, какие виды работы вас ждут, и в какой форме ваша работа на уроке будет оценена. -Попробуйте ответить на вопрос: «Какого результата вы хотите достичь на этом уроке?» и в своем оценочном листе в первой графе поставьте ту оценку, которую вы планируете получить за урок, согласно прописанным критериям. |
| 2. Актуализации знаний 5 мин | Поисковая деятельность | Организовывает выполнение практической работы. Фиксирует сделанные учениками выводы, организует их обсуждение, помогает сформулировать и доказать теорему. | Выполняют практическую работу, анализируют, доказывают, аргументируют свою точку зрения. | Взаимодействуют в процессе выполнения практической работы в парах, учатся находить взаимопонимание, достигать вместе поставленной цели. | Исследуют условия учебной задачи, обсуждают способы решения |
|
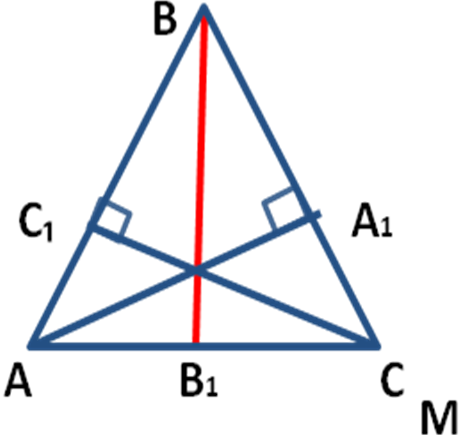
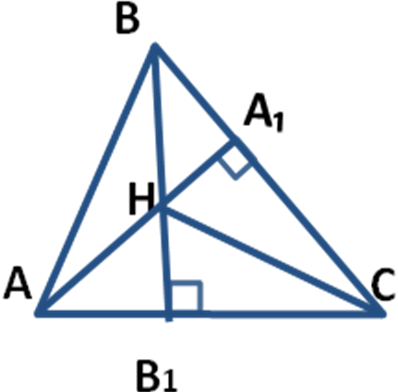
| Сегодня мы продолжим изучение темы «Замечательные точки треугольника» и познакомимся с теоремой о точке пересечения высот в треугольнике. Вспомните определение высоты в треугольнике. Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. Практическая работа. а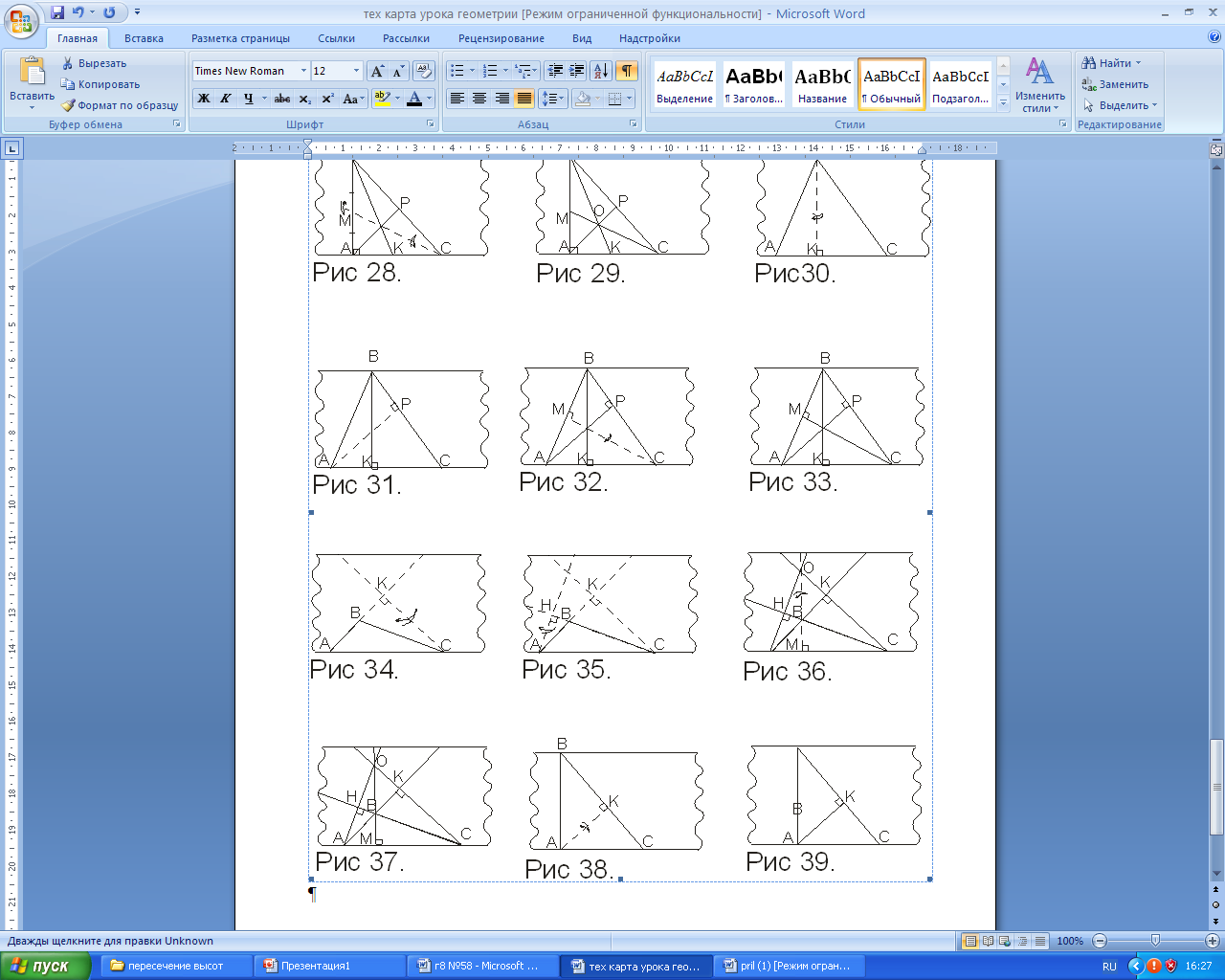 ) С помощью чертежного треугольника, постройте высоты в остроугольном треугольнике. ) С помощью чертежного треугольника, постройте высоты в остроугольном треугольнике. 1. Проведите ВВ1 АС 2. Проведите AА1 ВС. 3. Проведите СС1 АВ. Вывод: В остроугольном треугольнике все три высоты пересеклись в одной точке. Эта точка принадлежит треугольнику. 2) Постройте высоты в тупоугольном треугольнике. 1. Проведите ВВ1 АС, основание высоты лежит на продолжении АC. 2. Проведите AА1 ВС, основание высоты лежит на продолжении ВC. 3. Проведите CС1 AB. Продолжения высот тупоугольного треугольника пересеклись в одной точке Н. Вывод: В тупоугольном треугольнике все три продолжения высот пересеклись в одной точке. Эта точка расположена вне треугольника. в) Постройте высоты в прямоугольном треугольнике: 1. Проведите CС1 АB. 2. Проведите AА1 ВС. 3. Проведите BВ1 AC. Высоты прямоугольного треугольника пересеклись в одной точке Н. Вывод: В прямоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка принадлежит треугольнику и совпадает с вершиной прямого угла.
|
| 3. Изучения нового материала 10 мин. | Повторить теорему о серединном перпендикуляре к отрезку; свойство серединных перпендикуляров к сторонам треугольника. Доказать теорему о пересечении высот треугольника | Организует учебное взаимодействие учеников в ходе доказательства теоремы | Доказывают теорему о пересечении высот треугольника. | Воспринимают ответы обучающихся | Осуществляют самоконтроль Принимают и сохраняют учебную цель и задачу. |
|
| Прежде, чем мы приступите к доказательству этой теоремы, давайте вспомним основные понятия и свойства, которые мы будем использовать при доказательстве: - теорему о серединном перпендикуляре к отрезку; - свойство серединных перпендикуляров к сторонам треугольника. Теорема о пересечении высот треугольника. (Слайд ) Высоты треугольника (или их продолжения) пересекаются в одной точке. Д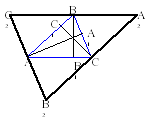 ано: ΔABC, ано: ΔABC, AA1^B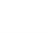
C, BB1^A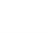
C, CC1^A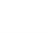
B. Доказать: O= AA1Ç BB1 Ç CC1. Доказательство: 1. Проведём: С2B2║BC, A2C2║AC, A2B2║AB так, что B Є A2C2, C Є A2B2, A Є B2C2. Получим Δ A2 B2 C2. 2. AB= A2C, AB= С2B2 точки A, B и C– середины сторон Δ A2 B2 C2, т.е. прямые АА1, BB1, CC1-серединные перпендикуляры к сторонам Δ A2 B2 C2Þ O= AA1Ç BB1 Ç CC1.
|
| 4. Физпауза 3 мин. | Мы хорошо потрудились и сейчас немного отдохнем. | Выполняют упражнения |
| 5. Этап закрепления изученного материала 15 мин. | Научить применять полученные знания при решении задач. | Организует решение задач по готовым чертежам; выполнение взаимопроверки; рейтинговую самостоятельную работу; разбор решения задач по готовым чертежам. | Применяют полученные знания для решения задач.. | Выполняют взаимопроверку доброжелательно и качественно. | Организовывают собственную самостоятельную деятельность. |
|
| 1. Решить по готовому чертежу задачи. 2. Взаимопроверка. 3. Выставление баллов в оценочный лист. 4. Выводы: точка пересечения биссектрис треугольника лежит внутри треугольника; точка пересечения медиан треугольника лежит внутри треугольника; точка пересечения серединных перпендикуляров треугольника лежит внутри треугольника; точка пересечения высот треугольника (или их продолжений) может лежать вне треугольника. 5. Решение задач разного уровня сложности по выбору учащихся: Базовый уровень – 3 балла; Повышенный уровень – 4 балла; Высокий уровень – 5 баллов. 6. Разбор решения задач по готовым чертежам. 7. Выставление баллов в оценочный лист.
|
| 6. Этап подведения итогов.
| Домашнее задание. рефлексия | Диагностическая работа (на выходе): - организация дифференцированной коррекционной работы,; - контрольно-оценивающая деятельность. | Отвечают на вопросы. | Рефлексия своих действий | Подводят итог; выставляют оценку согласно критериям. Выбирают уровень домашнего задания. |
|
| Наш урок подходит к концу, запишем домашнее задание и затем подведем итоги. На доске: Домашнее задание: П. 72-73; вопросы 15-20 стр.187; решить базовый уровень – повышенный уровень – высокий уровень – - на все ли вопросы мы получили ответы? - давайте ещё раз вспомним теорему о пересечении высот треугольника; - как называется точка пересечения высот треугольника? - где может располагаться ортоцентр треугольника? А где располагаются остальные три замечательные точки треугольника? Заканчиваем заполнение оценочных листов. Удалось ли вам достичь того результата, который вы запланировали в начале урока? Итог урока каждый из вас подведет с помощью короткой анкеты. Переверните оценочные листы и выразите своё отношение к уроку. Анкета Своей работой на уроке я доволен / не доволен Материал урока мне был понятен / не понятен Урок мне показался интересным / не интересным За урок я устал / не устал
|



Просмотр содержимого презентации
«пересечение высот»

Презентация выполнена учителем математики МБОУ гимназия № 35
Ленинского района
г. Ростова-на-Дону
Капустянской Еленой Витальевной

28 .0 4
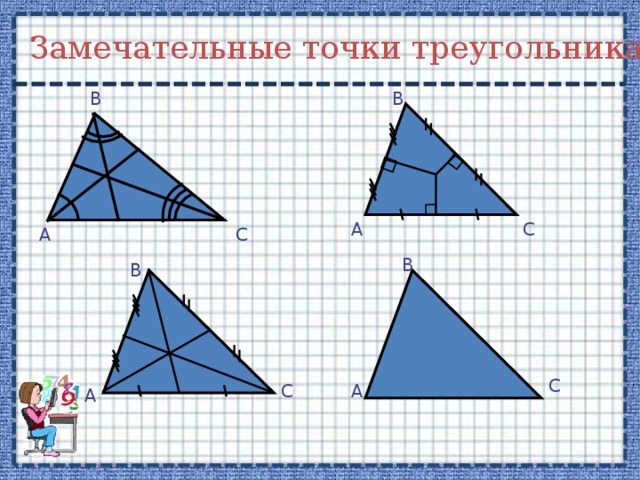
Замечательные точки треугольника
В
В
А
С
А
С
В
В
С
С
А
А

Вывод: В остроугольном треугольнике все три высоты пересеклись в одной точке. Эта точка принадлежит треугольнику.
Вывод: В тупоугольном треугольнике все три продолжения высот пересеклись в одной точке. Эта точка расположена вне треугольника.
Вывод: В прямоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка принадлежит треугольнику и совпадает с вершиной прямого угла.

Дано:
Δ ABC , AA 1 BC , BB 1 AC ,
CC 1 AB .
Доказать:
AA 1 BB 1 CC 1 =Н.
В
С 2
А 2
С 1
А 1
Н
Доказательство:
- Проведём: С 2 B 2 ║ BC , A 2 C 2 ║ AC , A 2 B 2 ║ AB .
Получим Δ A 2 B 2 C 2 ;
С
А
В 1
АВ A 2 C -параллелограмм,
A В= A 2 С
AC ║ A 2 В
В 2
А 2 C =В 2 C ;
АВ║ В 2 C
В C ║ A В 2
АВ C В 2 -параллелограмм,
A В=В 2 С
3) С C 1 серединный к A 2 В 2 ; ВВ 1 серединный к A 2 С 2 ; АА 1 серединный к С 2 В 2 ;
4) AA 1 BB 1 CC 1 =Н.

H
C
B 1
A
B
A 1
1 вариант
2 вариант
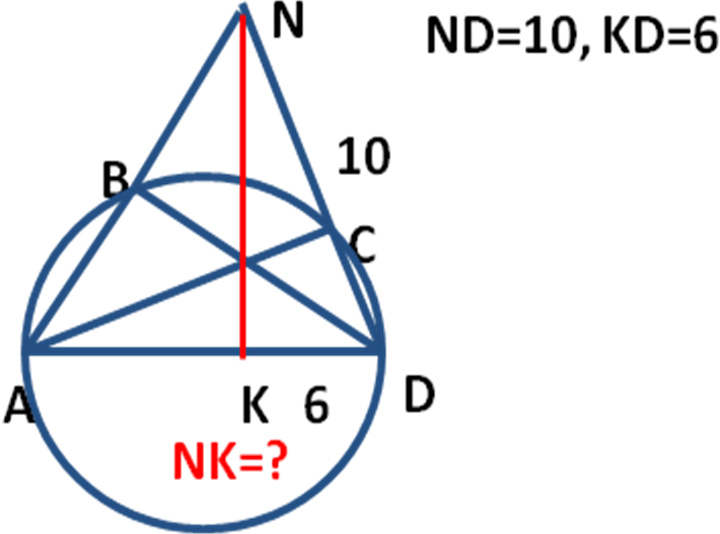
N
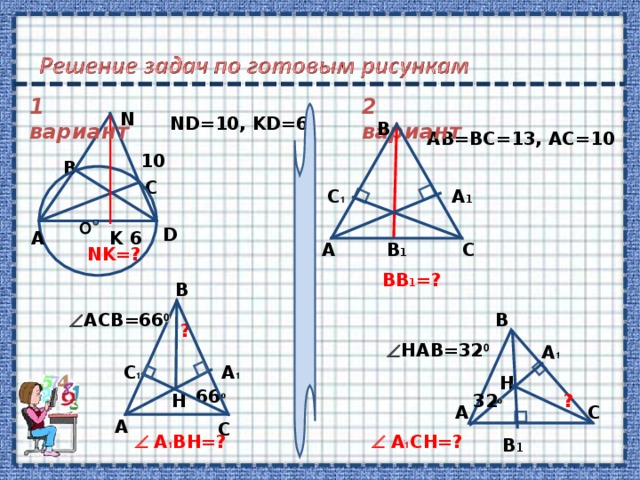
ND=10, KD=6
B
AB=BC=13, AC=10
10
B
C
A 1
C 1
О
D
А
K
6
А
B 1
C
NK=?
BB 1 =?
B
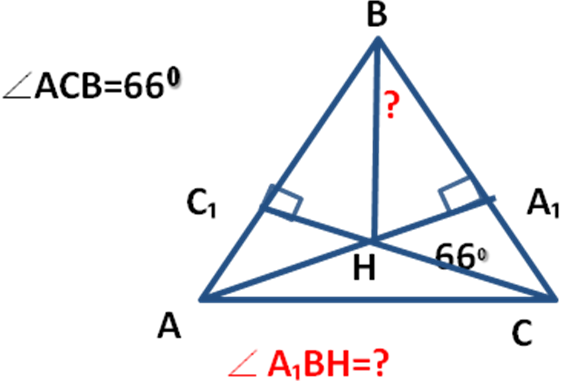
ACB=66 0
?
HAB=32 0
A 1
C 1
66 0
H
?
32 0
А
C
A 1 BH=?
A 1 CH=?


Вариант 2
Вариант 1

Домашнее задание:
П. 72-73; вопросы 15-20 стр.187-188;
решить:
базовый уровень – № 685;
повышенный уровень – № 681;
высокий уровень – № 688.
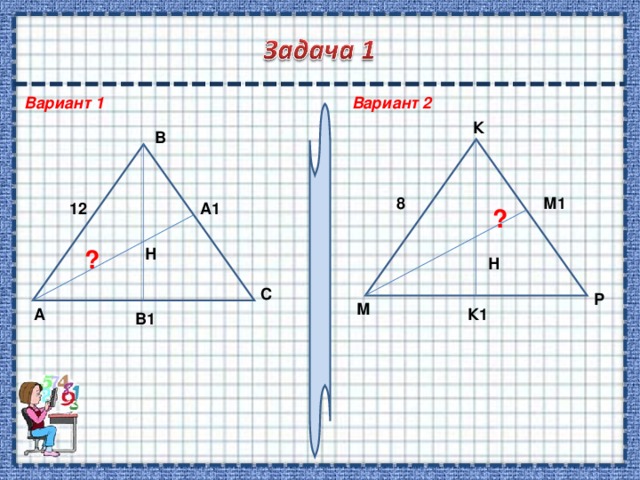
Вариант 1
Вариант 2
К
В
М1
8
А1
12
?
Н
?
Н
С
Р
М
К1
А
В1
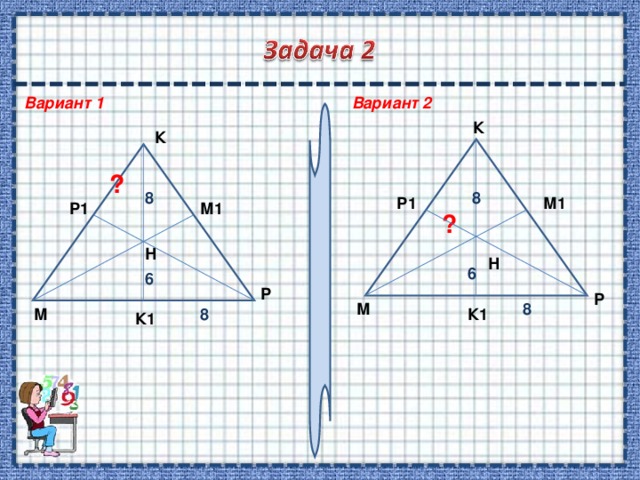
Вариант 2
Вариант 1
К
К
?
8
8
Р1
М1
Р1
М1
?
Н
Н
6
6
Р
Р
М
8
К1
М
8
К1

Вариант 1
Вариант 2
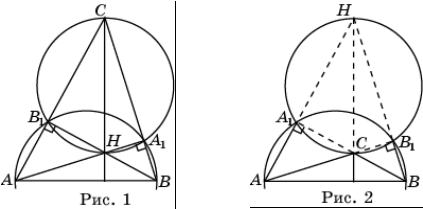
Прямые, содержащие высоты остроугольного треугольника ABC пересекаются в точке H (рис.1) . Известно, что CH = AB . Найдите угол ACB .
Прямые, содержащие высоты тупоугольного треугольника ABC пересекаются в точке H (рис. 2). Известно, что CH = AB . Найдите угол ACB .
?
?
Цели и задачи урока:
Предметные: расширить знания учащихся о треугольниках; практическим путем выяснить где пересекаются высоты треугольника (или их продолжения), доказать теорему о пересечении высот треугольника, научить решать задачи на применение нового материала.
Метапредметные:
регулятивные – развивать навыки самоорганизации, умение определить цель предстоящей познавательной деятельности, её вид, уровень сложности, пути достижения ожидаемого результата; развивать умение контролировать и оценивать свои действия.
познавательные – создавать условия для развития навыков самостоятельной познавательной деятельности; для развития навыков владения устной речью, способностью формулировать собственное мнение и аргументировать его, развивать логическое мышление, умение устанавливать причинно-следственные связи.
коммуникативные – способствовать развитию навыков организации учебного сотрудничества с учителем и одноклассниками, умений работать в паре, согласовывать свои действия, оказывать необходимую взаимопомощь друг другу.
Личностные – создавать условия для развития самосознания, самоопределения, позитивной оценки происходящих событий.

- Организационный.
- Актуализации знаний.
- Изучения нового материала.
- Физпауза.
- Закрепление изученного материала.
- Подведение итогов.

Использованная литература
- Атанасян Л.С. и др. Геометрия 7-9 классы. –
М:, Просвещение, 2008г.
2. Атанасян Л.С., Бутузов В.Ф. и др. «Изучение геометрии в 7-9 классе». Методические рекомендации. М:, Просвещение, 2007г.
3. Зив Б.Г., Мейлер В.М. «Дидактические материалы по геометрии. 8 кл». М:, Просвещение, 2007г.








 ) С помощью чертежного треугольника, постройте высоты в остроугольном треугольнике.
) С помощью чертежного треугольника, постройте высоты в остроугольном треугольнике. ано: ΔABC,
ано: ΔABC, 
























