| 1.Организационный момент.
2.Актуализация ранее полученных знаний. Используются репродуктивный, наглядный, словесный методы.
Фронтальная работа с классом, развитие коммуникативных способностей детей Формирование у учащихся навыков самоконтроля
Мотивация учебной деятельности учащихся
3. Закрепление предметных ЗУНов по теме «Линейная функция и её график» Используется частично – поисковый, наглядный, словесно-логический методы
Совершенствование навыков построения графиков. Формирование у учащихся навыков самоконтроля. 4. Элементы нового материала Фронтальная работа с классом, развитие коммуникативных способностей детей, Используется частично – поисковый, наглядный, словесно-логический методы.
5.Контроль усвоения полученных знаний с последующей взаимопроверкой Словесное поощрение учеников. Создание ситуации успеха.
6. Подведение итогов занятия
7. Домашнее задание.
8.Рефлексия
| Учитель приветствует детей, организует внимание.
-Какую тему вы изучали на прошлом занятии? -Сегодня мы продолжим работать над ней.
Учитель подводит детей к формулировке целей и задач занятия.
Обращает внимание обучающихся на эпиграф к уроку. -Что вы знаете о линейной функции? -Какой вид имеет формула, задающая линейную функцию? -Что такое k, b, x и y? -Что является графиком линейной функции? -Сколько точек необходимо для построения графика линейной функции?
Понятие функции первоначально возникло из решения практических задач. В частности формулы…(учитель демонстрирует формулы линейных зависимостей из разных областей жизнедеятельности человека).
Учитель делает акцент на межпредметные связи, имеющие место в данной теме.
Учитель обращает внимание на то, что у каждого обучающегося на парте есть набор заданий, необходимых для работы. В течении урока заполняется рабочий лист. Задание №1. Из данных функций выберите функции, являющиеся линейными.(Слайд 1) Задание №2.Назовите числа k и b в формулах линейных функций. (Слайд 1)
(Учитель поощряет лучшие ответы)
Задание №3. - Постройте графики функций у = 2х – 1 и y = -2x+3 .(Демонстрация слайда № 2)
- Внимательно посмотрите на ранее приведённые примеры, меняются ли значения k и b в этих функциях?
Создаём проблемную ситуацию: как угол наклона графика линейной функции к оси абсцисс связан со значением коэффициента k? (Работа со слайдом № 4).
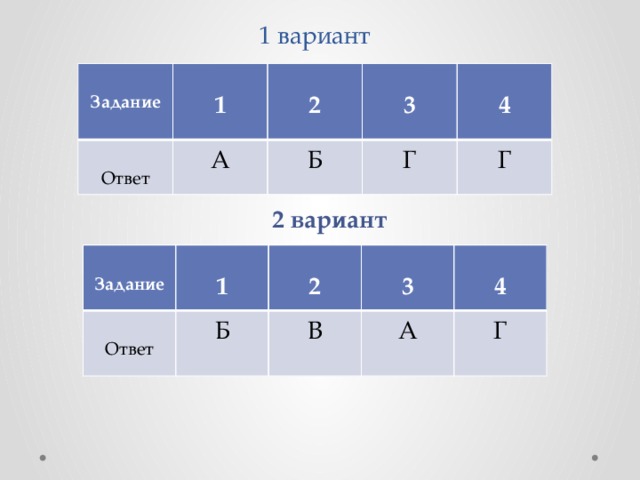
Задание №4. Некий обучающийся построил графики линейных функций. Проверьте правильность выполнения заданий. (4 варианта заданий)
Задание №5.Тестовое задание.
Учитель фронтально проверяет степень выполнения тестового задания. Выполнившие тест на 4 и 5 , получают на дом творческое задание. Тем, кто выполнил тест хуже, рекомендуется доработать тему и ,при необходимости, обратиться за консультацией к учителю математики.
Учитель поясняет домашнюю работу.
| Обучающиеся приветствуют учителя.
Отвечают на вопрос учителя.
Обучающиеся отвечают на вопросы учителя.
Обучающиеся определяют, какие величины находятся в линейной зависимости.
Делают вывод о широком практическом применении линейных зависимостей.
Выполняют задание в рабочем листе, сравнивают с эталоном
Выполняют задание в рабочем листе, сравнивают с эталоном
Задание выполняется самостоятельно по вариантам в рабочем листе. Одновременно двое обучающихся выполняют это задание у доски. Результаты сравниваются.
Делают вывод, что значения k и b в этих функциях меняются.
Делают вывод о зависимости угла наклона графика линейной функции к оси абсцисс от знака коэффициента k.Записывают его в рабочих листах.
Работа в парах с последующим объяснением ответа Одновременно два человека выполняют индивидуальное задание с оформлением на доске.
Выполняют тестовое задание по вариантам. Производят взаимопроверку работ
По результатам работы на уроке делают выводы. |