"Прямоугольник, ромб, квадрат".
9-й класс
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»
А. Н. Крылов
Тип урока: урок повторения, обобщения и систематизации
Цели урока:
Обучающие Повторить определение, свойства, признаки четырёхугольников – параллелограмма. Повторить определение, свойства прямоугольника, ромба и квадрата, учить применять их на практических задачах. Учить анализировать условие задачи, вести по результатам анализа построение, проводить исследование.
Развивающие Развивать умение планировать собственную деятельность, преодолевать трудности интеллектуального труда.
Формировать навыки обобщения и систематизации знаний по теме.
Воспитательные Формировать потребность к самоконтролю; навыки партнёрской деятельности в группе, в коллективе; навыков самостоятельного обучения. Развивать чувства долга и ответственности за результаты собственной деятельности.
Создать условия для реализации учебных потребностей каждого ученика в классе.
ХОД УРОКА
I . Мотивация к учебной деятельности и постановка целей урока
Задачи на моделирование (в этих задачах все используемые палочки одинаковы по длине).
1. Из пяти палочек без наложения составить 2 треугольника и четырехугольник.
|
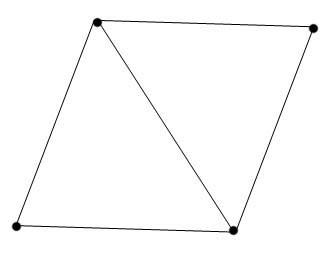
Рисунок 2
|
Определите:
а) вид полученных фигур (ромб и равносторонние треугольники);
б) углы четырехугольника ( ) )
|
2. Из 7 палочек без наложения составить 3 треугольника и 3 четырехугольника.
|
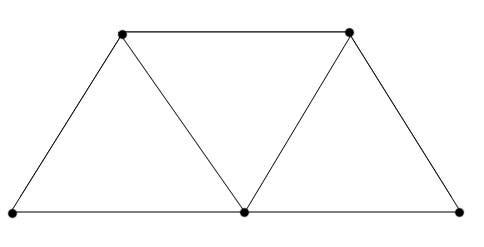
Рисунок 3
|
Определите:
а) вид полученных четырехугольников
(2 ромба и 1 равнобедренная трапеция);
б) углы трапеции.
|
3. Из 9 палочек составить 4 треугольника, 3 ромба, 2 трапеции и параллелограмм, не являющийся ромбом.
|
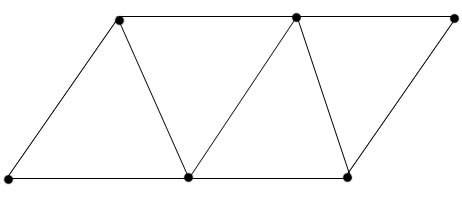
Рисунок 4
|
Определите:
а) периметр параллелограмма, если длина палочки равна а. (Р=6а)
|
4. Из 9 палочек составить 5 треугольников, 3 ромба, 3 трапеции.
|
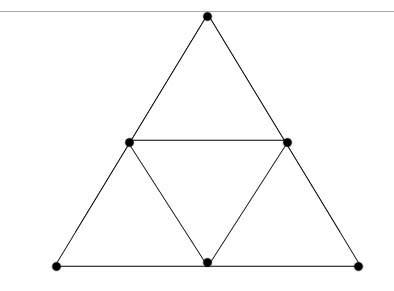
Рисунок 5
|
Определите:
а) сравните периметр большого треугольника и периметр параллелограмма. (Р треуг.=6а,
Р парал-ма= 4а)
|
5. Из 8 палочек составить квадрат, 2 треугольника и выпуклый шестиугольник.
|
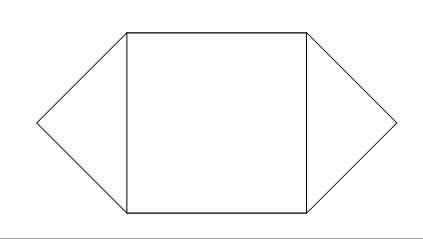
Рисунок 6
|
Определите:
а) определите чисто всех диагоналей (9)
|
Вывод: любой многоугольник можно составить из треугольников. Обратное утверждение тоже верно.
Разбивать можно не только диагоналями, но и другими отрезками. Например, медианами, биссектрисами, средними линиями.
II. Повторение, систематизация и обобщение теоретических знаний по теме. Работа с таблицей (самостоятельная работа) 
1.Игра «ДАНЕТКИ». Самостоятельная работа. Взаимопроверка по образцу.
1. Ромб – параллелограмм, у которого все углы прямые? (Нет)
2. Ромб – параллелограмм, у которого все стороны равны? (Да)
3. Прямоугольник – параллелограмм, у которого все углы равны? (Да)
4. Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны?
(Да)
5. Параллелограмм – четырехугольник, у которого диагонали точкой пересечения делятся пополам? (Да)
6. Прямоугольник – параллелограмм, у которого все стороны равны? (Нет)
7. Ромб – параллелограмм, у которого все углы прямые? (Нет)
8. Квадрат – ромб, у которого все углы прямые? (Да)
9. Параллелограмм – четырехугольник, у которого две противоположные стороны попарно равны? (Нет)
10. Параллелограмм – четырехугольник, у которого противоположные стороны попарно равны?
(Да)
2. Сказка-загадка
Собрались все четырехугольники на лесной поляне и стали решать, кто будет их королем. Долго спорили и никак не могли прийти к единому мнению. И вот один старый параллелограмм сказал: "Давайте все отправимся в царство четырехугольников. Кто придет первым, тот и будет королем". Все согласились. Рано утром отправились все в путешествие. На пути им встретилась река, которая сказал: "Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам". Часть четырехугольников осталась на берегу, остальные благополучно перебрались на тот берег и отправились дальше. На пути им встретилась высокая гора, которая сказала: "Я пропущу только тех, у кого диагонали равны". Несколько путешественников осталось у горы, остальные продолжили путь. Дошли до большого обрыва, над которым был узкий мост. Мост сказал "Меня перейдут только те, у кого диагонали пересекаются под прямым углом". По мосту прошел только один четырехугольник, который, добравшись до царства, был провозглашен королем.
Вопросы:
Кто стал королем? (Квадрат)
Кто был основным соперником? (Прямоугольник)
Кто первым выбыл из соревнования? (Трапеция)
Заполнить таблицу. Работа в парах. Самопроверка по образцу.
Прямоугольник. Ромб. Квадрат.
Свойства
|
| Паралле- лограмм | Прямо- угольник | Ромб | Квад- рат |
| 1.Противолежащие стороны параллельны и равны. |
|
|
|
|
| 2.Все стороны равны. |
|
|
|
|
| 3.Противолежащие углы равны, сумма соседних углов равна 180°. |
|
|
|
|
| 4.Все углы прямые. |
|
|
|
|
| 5.Диагонали пересекаются и точкой пересечения делятся пополам. |
|
|
|
|
| 6.Диагонали равны. |
|
|
|
|
| 7.Диагонали взаимно перпендикулярны и являются биссектрисами его углов. |
|
|
|
|
| 8. Сумма всех углов равна 360° |
|
|
|
|
Задание
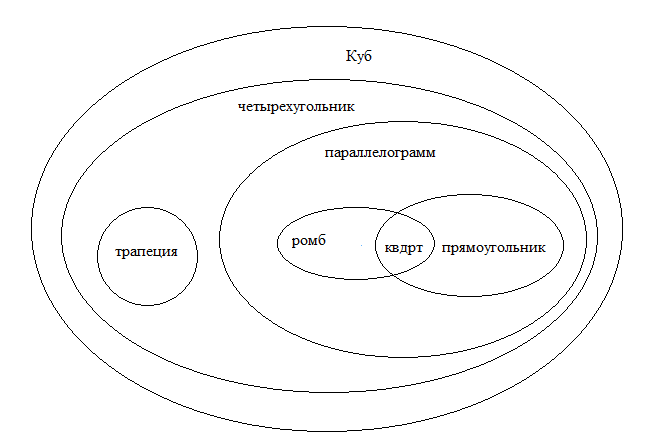
Систематизируя рассмотренные свойства данных фигур, цифрами отметить на рисунке количество известных свойств каждой фигуры
(Все фигуры имеют 4 свойства , параллелограмма, ромбы имеют дополнительно еще 3 свойства, прямоугольники – дополнительно 2 свойства, а квадраты имеют все свойства параллелограмма (4), дополнительно свойства ромба, прямоугольника – всего 9 свойств.)

3. Проверочный тест
Вариант 1.
1. Любой прямоугольник является:
а) ромбом; б) квадратом; в) параллелограммом; г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник - …
а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.
3. Ромб – это четырехугольник, в котором …
а) диагонали точкой пересечения делятся пополам и равны;
б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;
в) противолежащие углы равны, а противолежащие стороны параллельны;
г) нет правильного ответа.
Вариант 2.
1. Любой ромб является:
а) квадратом; б) прямоугольником; в) параллелограммом; г) нет правильного ответа.
2. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм - …
а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.
3. Прямоугольник – это четырехугольник, в котором …
а) противолежащие стороны параллельны, а диагонали равны;
б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
в) два угла прямые и две стороны равны;
г) нет правильного ответа.
Ответы к тесту:1 вариант: 1 – в); 2 – г); 3 – б).
2 вариант: 1 – в); 2 – а); 3 – а).
III. Решение задач (по готовым чертежам)

Назовите цвета :
параллелограммов,
прямоугольников,
квадратов, треугольников
1. Задача
На сторонах АВ и СD прямоугольника ABCD взяты точки К и М так, ч то АКСМ – ромб. Диагональ АС составляет со стороной АВ угол 30о. Найдите сторону ромба, если наибольшая сторона прямоугольника
то АКСМ – ромб. Диагональ АС составляет со стороной АВ угол 30о. Найдите сторону ромба, если наибольшая сторона прямоугольника
равна 3.
Дано: АВСD- прямоугольник, АВ=3, К- принадлежит АВ, М- принадлежит СD,  КАС=30о, АКСМ- ромб.
КАС=30о, АКСМ- ромб.
Найти АК.
Решение:
а) АКСМ- ромб, тогда АК=КС, ∆АКС- равнобедренный, значит  КСА=
КСА= КАС=30о,
КАС=30о,  АКС=120о,
АКС=120о,  ВКС=60о
ВКС=60о
б) ∆КВС- прямоугольный, в нем  ВКС=60о,
ВКС=60о,  КСВ=30о, тогда КВ=КС:2=АК:2
КСВ=30о, тогда КВ=КС:2=АК:2
в) Т.к. КВ=АК:2, АВ=АК+КВ=АК+АК:2=3*АК:2=3, то АК=2
Ответ: АК=2
2. Решение задач
А) Решение задач на готовых чертежах (устно)
1) Рис.1. АВСD – ромб. Найти: МD + DN.
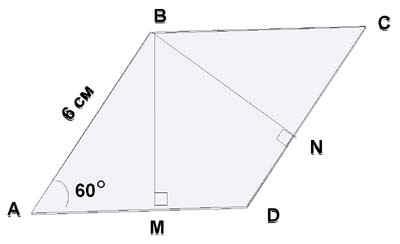
2) Рис.2. АВСD – ромб. Найти:  СВЕ.
СВЕ.
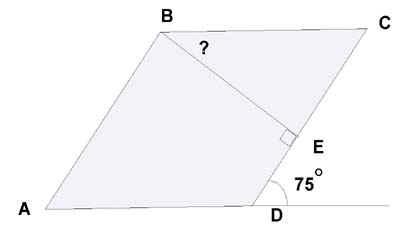
Ответы к задачам на готовых чертежах:
1) МD + DN = 6 см.
2)  СВЕ = 150.
СВЕ = 150.
Б) Решение задач у доски с краткой записью
1) Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 300 меньше другого.
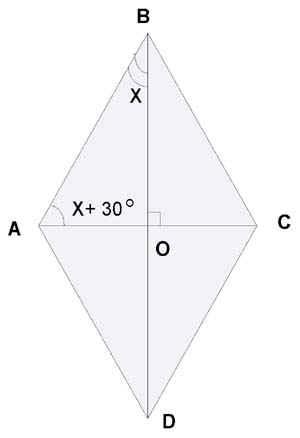
Решение:
Диагонали ромба взаимно перпендикулярны, поэтому треугольник АОВ – прямоугольный (рис.3). Пусть в ∆АОВ  АВО = х, тогда
АВО = х, тогда  ВАО = х + 300, значит
ВАО = х + 300, значит  АВО +
АВО +  ВАО = х + х + 300 = 900, и х = 300.
ВАО = х + х + 300 = 900, и х = 300.
 АВО = 300,
АВО = 300,  ВАО = 600, а т.к. диагонали ромба являются биссектрисами его углов, то
ВАО = 600, а т.к. диагонали ромба являются биссектрисами его углов, то  ВАD = 1200,
ВАD = 1200,  АВС = 600.
АВС = 600.
Противолежащие углы в ромбе равны, тогда  АDС =
АDС =  АВС = 600,
АВС = 600,  ВСD =
ВСD =  BAD = 1200.
BAD = 1200.
Ответ: 600, 1200, 600, 1200. Рис.3.
2) Угол между диагоналями прямоугольника равен 800 . Найдите углы между диагональю прямоугольника и его сторонами.
Решение:
Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит ВО = ВD/2 = АС/2 =АО и ∆АОВ – равнобедренный (рис.4.), тогда  ОАВ =
ОАВ =  ОВА = 500. В прямоугольнике все углы прямые, тогда
ОВА = 500. В прямоугольнике все углы прямые, тогда  ОАD =
ОАD =  ВАD -
ВАD -  ОАВ = 900 – 500 = 400.
ОАВ = 900 – 500 = 400.
Ответ: 500, 400.
3) В ромбе ABCD биссектриса угла ВAC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите угол АNВ, если  АМС = 1200 .
АМС = 1200 .
Решение:
В ромбе противолежащие углы равны и диагонали являются биссектрисами его углов, т.е.  ВАС =
ВАС =  ВАD : 2 =
ВАD : 2 = ВСD : 2 =
ВСD : 2 =  ВСА. Т.к. АМ – биссектриса
ВСА. Т.к. АМ – биссектриса  ВАС, а
ВАС, а  ВАС =
ВАС =  ВСА, то
ВСА, то  МАС =
МАС =  МСА : 2.
МСА : 2.
В треугольнике АМС  МАС +
МАС +  МСА = 1800 -
МСА = 1800 -  АМС = 1800 -1200 = 600.
АМС = 1800 -1200 = 600.  МАС =
МАС =  МСА : 2, тогда
МСА : 2, тогда  МАС = 200,
МАС = 200,  ВАС = 400.
ВАС = 400.
В ромбе диагонали взаимно перпендикулярны, треугольник АОВ – прямоугольный,  АВО = 900 -
АВО = 900 -  ВАО = 500. Рис.5.
ВАО = 500. Рис.5.
В треугольнике АВN  BAN =
BAN =  МАС = 200,
МАС = 200,  ABN = 500, тогда
ABN = 500, тогда
 ANB = 1800 – (200 + 500) = 1100.
ANB = 1800 – (200 + 500) = 1100.
Ответ:  ANB = 1100.
ANB = 1100.
3.Самостоятельная работа по карточкам (разноуровневые задачи)
1) В ромбе АВСD диагонали пересекаются в точке О,  А = 320. Найдите углы треугольника ВОС.
А = 320. Найдите углы треугольника ВОС.
Решение:
а) Рис.6.  А =
А =  С = 320; СО – биссектриса
С = 320; СО – биссектриса  С,
С,  ОСВ = 16о;
ОСВ = 16о;
б) Треугольник СОВ – прямоугольный,  ВОС = 900,
ВОС = 900,  ОСВ = 16о,
ОСВ = 16о,  ОВС = 740.
ОВС = 740.
Ответ: 900, 160, 740.
2) В прямоугольнике АВСD О – точка пересечения диагоналей, ВН и DЕ – высоты треугольников АВО и СОD соответственно,  ВОН = 600 , АН = 5 см. Найдите ОЕ.
ВОН = 600 , АН = 5 см. Найдите ОЕ.
Решение:
а) Треугольник АВО – равнобедренный (рис.7.), ВО = ОА т.к. в прямоугольнике диагонали равны и точкой пересечения делятся пополам, а т.к.  ВОА = 600, то ∆АВО – равносторонний, поэтому высота ВН – медиана треугольника АВО, тогда ОН = 5 см.
ВОА = 600, то ∆АВО – равносторонний, поэтому высота ВН – медиана треугольника АВО, тогда ОН = 5 см.
б) Треугольник ОВН = треугольнику ОDЕ ( по стороне и двум прилежащим углам ВО = ОD,  ВОН =
ВОН =  DОЕ – вертикальные,
DОЕ – вертикальные,  ОВН =
ОВН =  ОDЕ – накрест лежащие при параллельных ВН и DЕ и секущей ВD).
ОDЕ – накрест лежащие при параллельных ВН и DЕ и секущей ВD).
Из равенства треугольников следует равенство сторон
ОН = ОЕ = 5 см.
Ответ: ОЕ = 5 см.
Дополнительная задача
В ромбе АВСD угол В тупой. На стороне АD взята точка К, ВК АD. Прямые ВК и АС пересекаются в точке О, АС = 2ВК. Найдите угол АОВ.
АD. Прямые ВК и АС пересекаются в точке О, АС = 2ВК. Найдите угол АОВ.
Решение:
а) Проведем АЕ  АD (рис.8), тогда КВ = АЕ, АС = 2АЕ,
АD (рис.8), тогда КВ = АЕ, АС = 2АЕ,  АСЕ = 300.
АСЕ = 300.
б)  СОВ = 600,
СОВ = 600,  АОВ = 1200.
АОВ = 1200.
Ответ: 1200.
V. Итог. Фронтально. Устно.
В следующих предложениях заменить многоточие словами: «необходимо и достаточно», «необходимо, но не достаточно», «достаточно, но необходимо».
1) Для того, чтобы четырехугольник был прямоугольником … (чтобы его диагонали были равны).
2) Для того, чтобы четырехугольник был параллелограммом … (чтобы все его стороны были равны).
3) Для того, чтобы четырехугольник был ромбом …( чтобы его диагонали были взаимно перпендикулярны и в точке пересечения делились пополам).
IV. Рефлексия деятельности (соотнесение результатов с поставленными целями урока) Определить характер своей работы на уроке, выбрав одно из трех высказываний:
1)Я выполнял тяжелую для меня работу.
2)Я добросовестно трудился.
3)Я возводил храм науки
Домашнее задание.
Повторить п.
Решить:
1. Периметр прямоугольника равен 48 см. Найдите его стороны, если они относятся как 1:2.
2. Диагональ ромба образует с одной из его сторон угол 40°. Найдите углы ромба.
3. В четырехугольнике ABCD отрезок АО - медиана треугольника ABD, отрезок ВО - медиана треугольника АВС. Определите вид четырехугольника.
4. Составить КЛАСТЕР «ЧЕТЫРЕХУГОЛЬНИКИ»
15














 то АКСМ – ромб. Диагональ АС составляет со стороной АВ угол 30о. Найдите сторону ромба, если наибольшая сторона прямоугольника
то АКСМ – ромб. Диагональ АС составляет со стороной АВ угол 30о. Найдите сторону ромба, если наибольшая сторона прямоугольника 












