Планиметрия .11 класс.
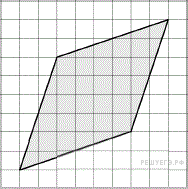
| 1. Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
| 
|
| 2. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 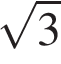 . .
| 
|
| 3. Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (8; 4), (8; 8), (2; 10). |
|
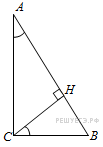
| 4. В треугольнике  угол угол 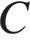 равен 90°, равен 90°,  – высота, – высота,  , , 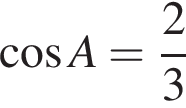 . Найдите . Найдите 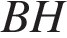 . .
| 
|
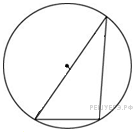
| 5. Найдите хорду, на которую опирается угол  , вписанный в окружность радиуса 3. , вписанный в окружность радиуса 3. .
| 
|
| 6. Сумма трёх углов выпуклого четырёхугольника равна 322°. Найдите его четвёртый угол. Ответ дайте в градусах | 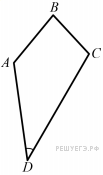
|
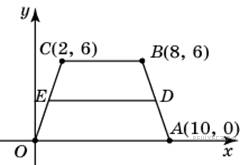
| 7. Точки O(0; 0), A(10; 0), B(8; 6), C(2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
| 
|
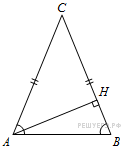
| 8. В треугольнике   , ,  – высота, – высота, 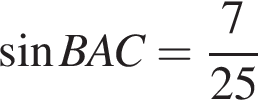 . Найдите . Найдите 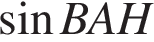 . .
| 
|
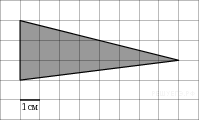
| 9. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
| 
|
| 10. В треугольнике 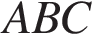  , высота , высота  равна 4, угол равна 4, угол 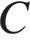 равен равен  . Найдите . Найдите  . .
| |
| 11.Острые углы прямоугольного треугольника равны 85° и 5°. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах. | |
| 12. Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). В ответе запишите 1 см (см. рис.). В ответе запишите  . . | |
| 13. На клетчатой бумаге с клетками размером 1 см  1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. | |
| 14. В треугольнике 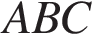 проведены медиана проведены медиана  и высота и высота 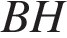 . Известно, что и . Найдите . Известно, что и . Найдите  . .
| |
| 15. Найдите угловой коэффициент прямой, проходящей через точки с координатами  и и |
| 16. Найдите среднюю линию трапеции, если ее основания равны 30 и 16. | |
| 17. Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). В ответе запишите 1 см (см. рис.). В ответе запишите  . .
| |
| 18. Точки O(0; 0), A(6; 8), B(6; 2), C(0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. | |
| 19. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции. | |
| 20. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции. | |
| 21. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах. | |
| 22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности. | |
| 23. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону. | |
| 1. AC и BD — диаметры окружности с центром O. Угол ACB равен 25°. Найдите угол AOD. Ответ дайте в градусах | |
| 2. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 25 , AO = 65 . | |
| 3. На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 67. Найдите длину большей дуги.
| |
| 4. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB Найдите угол ACB, если угол AOB равен 113°. Ответ дайте в градусах | |
| 5. На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 88. Найдите длину большей дуги. | |
| 6. AC и BD — диаметры окружности с центром O. Угол ACB равен 19°. Найдите угол AOD. Ответ дайте в градусах.
| |
| 7. На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 91. Найдите длину большей дуги | |
| 8. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 155°. Найдите величину угла BOC. Ответ дайте в градусах | |
| 9. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 86°. Найдите вписанный угол ACB. Ответ дайте в градусах. | |
| | |
| | |
| |

























