Погрешность и точность приближения

Автор: Софронова Наталия Андреевна,

учитель математики МОУ «Упшинская ООШ»

Оршанского района Республики Марий Эл

( К учебнику Ю.А.Макарычева Алгебра 8)

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

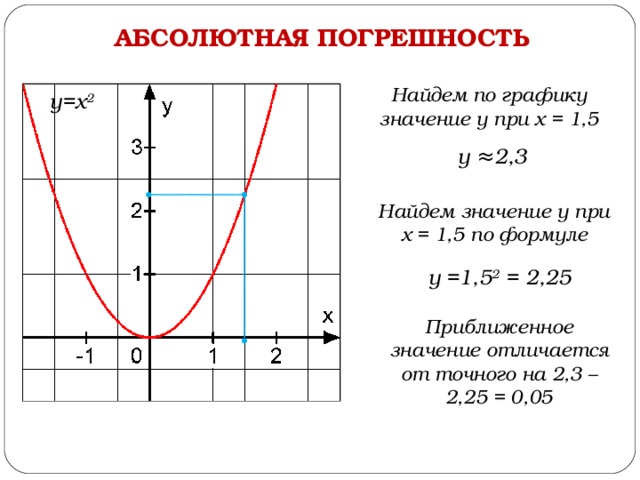
Найдем по графику значение у при х = 1,5

у=х 2

у ≈2,3

Найдем значение у при х = 1,5 по формуле

у =1,5 2 = 2,25

Приближенное значение отличается от точного на 2,3 – 2,25 = 0,05

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

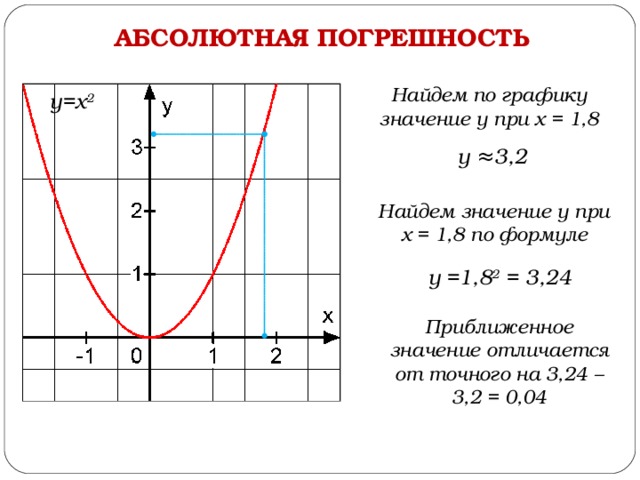
Найдем по графику значение у при х = 1,8

у=х 2

у ≈3,2

Найдем значение у при х = 1,8 по формуле

у =1,8 2 = 3,24

Приближенное значение отличается от точного на 3,24 – 3,2 = 0,04

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

х

1,5

Точное значение у

(по формуле)

1,8

2,25

Приближенное значение у (по графику)

3,24

2,3

3,2

у=х 2

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

у = 2,3 А.П. = |2,25 – 2,3| = |- 0,0 5| = 0,05

у = 3,2 А.П. = |3,24 – 3,2| = | 0,0 4| = 0,04

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 1 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите абсолютную погрешность приближенного значения.

Решение. 1 6 ,38 ≈ 16

16,38 – точное значение;

16 – приближенное значение.

А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 2 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите абсолютную погрешность приближенного значения.

Решение. 10 6 7 ≈ 1070

1067 – точное значение;

1070 – приближенное значение.

А.П. = | 1067 – 1070 | = |-3| = 3

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 3 . Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до десятых и найдите абсолютную погрешность приближенного значения.

Решение. 2, 1 3 ≈ 2,1

2,13 – точное значение;

2,1 – приближенное значение.

А.П. = | 2,13 – 2,1 | = | 0,03 | = 0,03

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Пример 4 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите абсолютную погрешность приближенного значения.

Решение.

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

Всегда ли можно найти абсолютную погрешность ?

АВ ≈ 5,3 см

Найдем длину отрезка АВ

А

В

Точного значения длины отрезка АВ мы определить не можем, поэтому и абсолютную погрешность приближенного значения найти невозможно.

В подобных случаях в качестве погрешности указывают такое число, больше которого абсолютная погрешность быть не может.

В нашем примере в качестве такого числа можно взять число 0,1.

ПОЧЕМУ? Цена деления линейки равна 0,1 см и поэтому абсолютная погрешность приближенного значения 5,3 не больше 0,1.

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

А

В

Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в санти-метрах) с точностью до 0,1

АВ ≈ 5,3 см

t ≈ 28 0 с точностью до 1

t ≈ 14 0 с точностью до 2

Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4

Рис.2

Рис.1

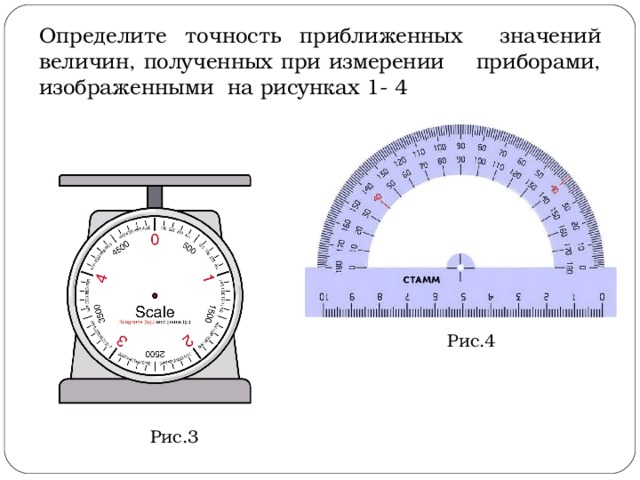
Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4

Рис.4

Рис.3

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в сантиметрах) с точностью до 0,1

АВ ≈ 5,3 см

Если х ≈ а и абсолютная погрешность приближенного значения не превосходит некоторого числа h , то число а называют приближенным значением х с точностью до h

х ≈ а с точностью до h

х = а ± h

Длина рулона 10,5 ± 0,5

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

А

В

АВ ≈ 5,3 см

с точностью до 0,1

t ≈ 28 0 с точностью до 1

t ≈ 14 0

с точностью до 2

Определение . Относительной погрешностью (точностью) приближенного значения называется отношение абсолютной погрешности (точности) к модулю приближенного значения

Для оценки качества измерения можно использовать определения относительной погрешности и относительной точности

l = 100,0 ± 0,1

b = 0,4 ± 0,1

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения

Пример 5 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите относительную погрешность приближенного значения.

Решение. 1 6 ,38 ≈ 16

16,38 – точное значение;

16 – приближенное значение.

А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения

Пример 6 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите относительную погрешность приближенного значения.

Решение. 10 6 7 ≈ 1070

1067 – точное значение;

1070 – приближенное значение.

А.П. = | 1067 – 1070 | = |-3| = 3

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Пример 7 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите относительную погрешность приближенного значения.

Решение.