Показательные уравнения.
Показательным называется уравнение, содержащее переменную в показателе степени.
Например, 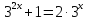
Простейшим показательным уравнением называется уравнение, вида 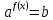 .
.
Решение любого показательного уравнения сводится к решению простейших показательных уравнений.
Методы решения показательных уравнений.
метод уравнивания показателей;
метод введения новой переменной;
метод разложения на множители;
функционально-графический метод;
метод почленного деления;
метод группировки.
Разберём каждый из этих методов отдельно.
Метод уравнивания показателей основывается на том свойстве, что, если основания степеней равны, то равны и показатели степеней. Поэтому при использовании данного метода необходимо левую и правую часть уравнения привести к степени с одинаковыми основаниями. Затем приравниваем показатели и решаем получившееся уравнение.
Например, 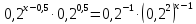
Используя свойства степеней, упрощаем выражения в обеих частях уравнения.
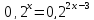
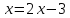
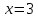
Ответ: 3
Метод введения новой переменной используется в случае, когда после упрощения обеих частей уравнения появилась возможность обозначить какую-то степень другой переменной и, при этом, все остальные степени также будут выражаться через введённую переменную.
Например, 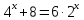
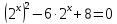
Введём новую переменную: 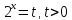 , тогда уравнение принимает вид:
, тогда уравнение принимает вид:
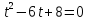
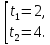
Возвращаемся к исходной переменной:
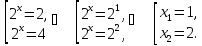
Ответ: 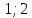 .
.
Метод разложения на множители, в частности, вынесения общего множителя за скобки, используется в том случае, когда степени, входящие в уравнение имеют одинаковые основания и коэффициенты перед переменной в показателе степени также одинаковы.
Например, 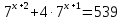
Оба слагаемых, стоящих в правой части уравнения, имеют общий множитель 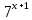 . Вынесем его за скобки (напомним, что вынести за скобки – значит разделить каждое слагаемое на этот общий множитель, а при делении степеней показатели вычитаются).
. Вынесем его за скобки (напомним, что вынести за скобки – значит разделить каждое слагаемое на этот общий множитель, а при делении степеней показатели вычитаются).
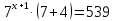
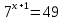
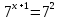
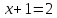
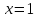
Ответ: 1.
Функционально-графический метод используется обычно в тех случаях, когда уравнение имеет смешанный тип, т.е. в нём присутствуют различные функции. Тогда необходимо преобразовать уравнение, чтобы в разных его частях находились разные функции. Построить графики этих функций и найти их точки пересечения. Абсциссы этих точек и будут корнями данного уравнения.
Например, 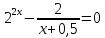
Преобразуем данное уравнение:
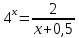
Построим графики функций, стоящих в разных частях уравнения.
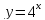 – показательная функция, график проходит через точку
– показательная функция, график проходит через точку 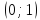 , возрастающий на всей области определения, т.к.
, возрастающий на всей области определения, т.к. 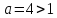 , дополнительные точки .
, дополнительные точки .
 – обратная пропорциональность, графиком является гипербола, которая получается из графика функции
– обратная пропорциональность, графиком является гипербола, которая получается из графика функции  смещением вдоль оси Ох на 0,5 ед. отрезков влево. Дополнительные точки для функции
смещением вдоль оси Ох на 0,5 ед. отрезков влево. Дополнительные точки для функции  .
.
График обратной пропорциональности достаточно построить только в I четверти, т.к. график показательной функции не опускается ниже оси Ох.
Графики этих функций пересекаются в точке  , значит, корнем исходного уравнения является
, значит, корнем исходного уравнения является  . Для убедительности, можно выполнить проверку.
. Для убедительности, можно выполнить проверку.



Равенство верное, значит, действительно, 
Ответ: 
Метод почленного деления заключается в том, чтобы разделить каждый член уравнения, содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Он применяется для решения однородных показательных уравнений.
Например, 
Разделим обе части уравнения на  . Это возможно сделать, т.к. значение показательной функции не может быть равным нулю.
. Это возможно сделать, т.к. значение показательной функции не может быть равным нулю.

Теперь можно сделать замену переменной:

Решив это квадратное уравнение, находим корни:
Возвращаемся к исходной переменной:

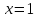
Ответ: 1.
Метод группировки заключается в том, чтобы собрать степени с одинаковыми основаниями в одной части уравнения, а затем разделить обе части уравнения на одну из степеней.
Например, 


Разделим обе части уравнения на  , получим уравнение:
, получим уравнение:

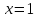
Ответ: 1.
Свойства степеней с вещественным показателем.
Степени с вещественными показателями обладают такими же свойствами, что и степени с рациональными показателями. Освежим их в памяти.






Решить графически уравнение:
Решить уравнение:
Решить уравнение:
Решить уравнение:
Решить уравнение:
Найти корни уравнения:
Решить уравнения:
При каждом значении параметра  определить число корней уравнения:
определить число корней уравнения:
Найти значение параметра  , при котором уравнение имеет два различных корня.
, при котором уравнение имеет два различных корня.
Найти значения параметра  , при которых уравнение не имеет корней.
, при которых уравнение не имеет корней.
7







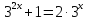
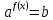 .
.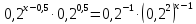
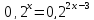
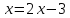
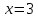
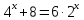
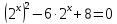
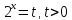 , тогда уравнение принимает вид:
, тогда уравнение принимает вид: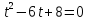
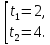
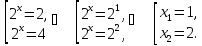
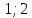 .
.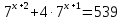
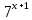 . Вынесем его за скобки (напомним, что вынести за скобки – значит разделить каждое слагаемое на этот общий множитель, а при делении степеней показатели вычитаются).
. Вынесем его за скобки (напомним, что вынести за скобки – значит разделить каждое слагаемое на этот общий множитель, а при делении степеней показатели вычитаются).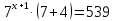
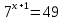
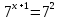
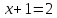
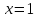
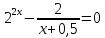
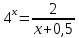
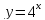 – показательная функция, график проходит через точку
– показательная функция, график проходит через точку 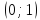 , возрастающий на всей области определения, т.к.
, возрастающий на всей области определения, т.к. 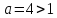 , дополнительные точки .
, дополнительные точки .



















