"Понятие объема. Объем прямоугольного параллелепипеда"

Объемы тел

Тема урока:

Понятие объема. Объем прямоугольного параллелепипеда

Величина части пространства, занимаемого геометрическим телом , называется объемом этого тела

Английские меры объема

• Бушель - 36,4 дм 3
• Галлон -4,5 дм 3
• Баррель (сухой)-
• 115,628 дм 3
• Баррель (нефтяной)-
• 158,988 дм 3
• Английский баррель для сыпучих веществ 163,65 дм 3

Русские меры объема

• Ведро - 12 дм 3
• Бочка - 490 дм 3
• Штоф - 1,23 дм 3 = 10 чарок
• Чарка -0,123 дм 3 =0,1 штофа= = 2 шкалика
• Шкалик -0,06 дм 3 = 0,5 чарки

Единицы объема

За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков.

Куб с ребром 1 см называют кубическим сантиметром и обозначают см 3 .

Свойства объемов

1 0 . Равные тела имеют равные объемы

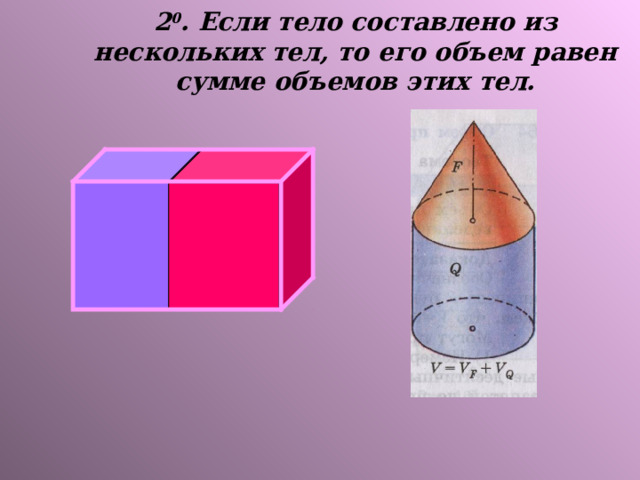
2 0 . Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.

АРХИМЕД (ок. 287-212 гг. до н.э.)

• На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3: 2.
• Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.

Объем прямоугольного параллелепипеда . Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений .

Следствие 1. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту Следствие 2. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту .

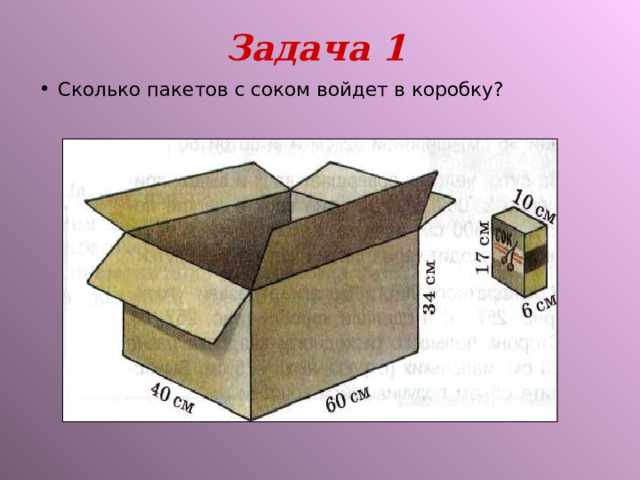
Задача 1

• Сколько пакетов с соком войдет в коробку?

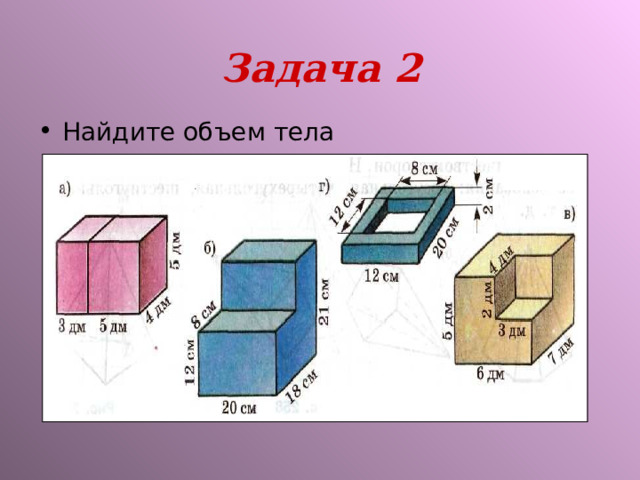
Задача 2

• Найдите объем тела

Задача 3

Сколько литров воды вмещает бак, имеющий форму куба с ребром 6 дм?

Задача 4

За сутки человек совершает вдох и выдох примерно 23 000 раз. За один вдох в легкие поступает 500 см 3 воздуха. Какой объем воздуха ( в литрах) проходит через легкие человека за сутки?

Задача 5

Больному прописали глазные капли, по 2 капли 3 раза в день в оба глаза. Во флаконе 10 мл лекарства. Объем капли 1 / 9 мл. Хватит ли одного флакона на неделю?

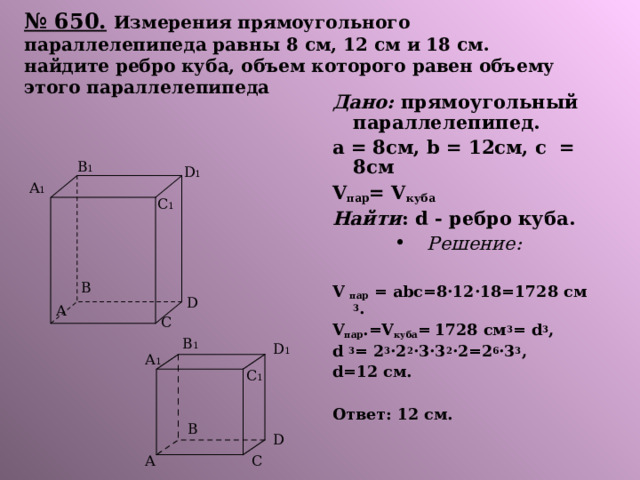
№ 650. Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. найдите ребро куба, объем которого равен объему этого параллелепипеда

Дано: прямоугольный параллелепипед.

а = 8см, b = 12см, с = 8см

V пар = V куба

Найти : d - ребро куба.

• Решение:

V пар = abc=8·12·18=1728 c м 3 .

V пар .=V куба = 1728 c м 3 = d 3 ,

d 3 = 2 3 ·2 2 ·3·3 2 ·2=2 6 ·3 3 ,

d=12 см.

Ответ: 12 см.

B 1

D 1

A 1

C 1

B

D

A

C

B 1

D 1

A 1

C 1

B

D

A

C

№ 653 . Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30 0 с плоскостью боковой грани и угол в 45 0 с боковым ребром. Найдите объем прямоугольного параллелепипеда.

Дано : ABCDA 1 B 1 C 1 D 1 - прямоугольный параллелепипед,. B 1 D - диагональ, B 1 D = 18 см,  (B 1 D; (АВВ 1 )) = 30 0 ,  B 1 D D 1 = 45 0

Найти: V параллелепипеда

• Решение

1 )Δ В 1 ВА – прямоугольный, т.к. В 1 В  АВ (по условию АВС DA 1 B 1 C 1 D 1 – прямоугольный параллелепипед).

 Δ B 1 AD -прямоульный, т.е. В 1 А = ПР ( АА1В ) B 1 D,

• 1 )Δ В 1 ВА – прямоугольный, т.к. В 1 В  АВ (по условию АВС DA 1 B 1 C 1 D 1 – прямоугольный параллелепипед).  Δ B 1 AD -прямоульный, т.е. В 1 А = ПР ( АА1В ) B 1 D,
• 1 )Δ В 1 ВА – прямоугольный, т.к. В 1 В  АВ (по условию АВС DA 1 B 1 C 1 D 1 – прямоугольный параллелепипед).  Δ B 1 AD -прямоульный, т.е. В 1 А = ПР ( АА1В ) B 1 D,

 ( B 1 D; (AA 1 B 1 )) =  DB 1 A = 30 0 .

2) Δ B 1 AD - прямоугольный c углом в 30 0 : AD = 9 см.

• 2) Δ B 1 AD - прямоугольный c углом в 30 0 : AD = 9 см.
• 2) Δ B 1 AD - прямоугольный c углом в 30 0 : AD = 9 см.

3) Δ B 1 D 1 D – прямоугольный, т.к.

• 3) Δ B 1 D 1 D – прямоугольный, т.к.
• 3) Δ B 1 D 1 D – прямоугольный, т.к.

4)По свойству диагонали прямоугольного параллелепипеда B 1 D 2 =AD 2 +DC 2 +DD 1 2 .

• 4)По свойству диагонали прямоугольного параллелепипеда B 1 D 2 =AD 2 +DC 2 +DD 1 2 .
• 4)По свойству диагонали прямоугольного параллелепипеда B 1 D 2 =AD 2 +DC 2 +DD 1 2 .

Ответ: см 3

C 1

B 1

A 1

D 1

B

C

D

A

Домашнее задание

• п. 63, п. 64

• № 643, №648(А)

• № 657, №660(В)

• ! Придумать задачу с практическим содержанием на нахождение объема прямоугольного параллелепипеда, решить ее