Позиционные и непозиционные системы счисления

Позиционные и непозиционные системы счисления

Способ наименования и записи чисел

принято называть системой счисления

Система счисления , в которой значения цифры зависят от ее места ( позиции ) в ряду цифр, изображающих число называется позиционной .

Система счисления , в которой значения цифры

Не зависят от ее места ( позиции ) в ряду цифр,

изображающих число называется непозиционной .

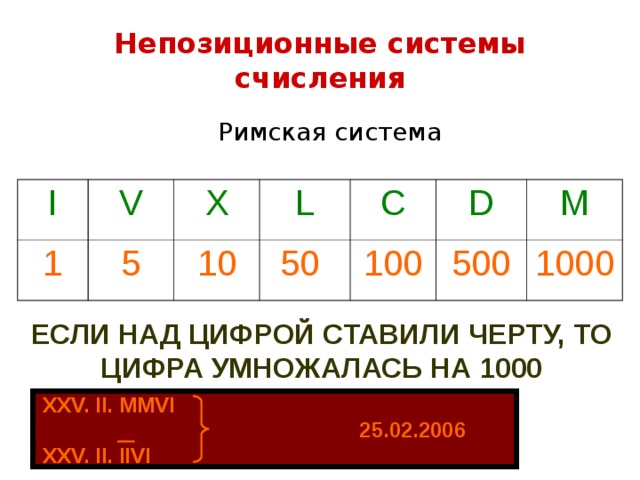
Непозиционные системы счисления

Римская система

I

V

1

5

X

L

10

C

50

D

100

M

500

1000

ЕСЛИ НАД ЦИФРОЙ СТАВИЛИ ЧЕРТУ, ТО ЦИФРА УМНОЖАЛАСЬ НА 1000

XXV. II. MMVI

25.02.2006

XXV. II. IIVI

Позиционные системы счисления

Позиции в позиционных системах счисления называются разрядами:

от 0 до бесконечности справа налево в целой части числа.

• Позиции в позиционных системах счисления называются разрядами: от 0 до бесконечности справа налево в целой части числа.

Например: 328

8 – нулевой разряд

2 – первый разряд

3 – второй разряд

Общепризнанной позиционной системой счисления является

ДЕСЯТИЧНАЯ

Позиционные системы счисления

Для простоты восприятия различных систем в индексе числа будем указывать основание системы:

3А65 16 – шестнадцатеричная

13427 8 – восьмеричная

11010110 2 – двоичная

Введем обозначения чисел различных систем счисления:

B 2 – ДВОИЧНЫЕ ЧИСЛА

D 10 – ДЕСЯТИЧНЫЕ ЧИСЛА

O 8 – ВОСЬМЕРИЧНЫЕ ЧИСЛА

H 16 – ШЕСТНАДЦАТЕРИЧНЫЕ

Запись вида Н 16 D 10 означает перевод числа шестнадцатеричного в десятичное

ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ

В записи десятичных чисел мы используем 10 цифр

(от 0 до 9).

Вообще запись числа означает представление этого числа в виде суммы степеней основания 10 с различными коэффициентами.

12 587 10 =1 · 10 4 + 2 · 10 3 + 5 · 10 2 + 8 · 10 1 + 7 · 10 0

Разложите самостоятельно:

1 вариант: 65782 10

2 вариант: 35921 10

ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ

Двоичная система счисления – это позиционная

система с основанием два. Для изображения чисел

в этой системе требуется лишь две цифры:0 и 1.

Таблицы сложения и умножения

х

+

0

0

0

0

1

0

1

1

0

1

0

1

1

0

10

1

Перевод чисел

Переведем число 395,375 10 в двоичную систему счисления.

Перевод производится в два этапа:

1) перевод целой части; 2) перевод дробной части.

395

197

1

1

98

0

49

1

24

12

0

0

6

0

3

1

1

1

,

0,

375

75

1,

5

1,

х2

:2

395,375 10 =110001011,011 2

Перевод чисел

Еще один пример для закрепления:

Перевести из D 10 в B 2 число 13,6 с точностью до четырех знаков после запятой.

При переводе дробной части

Опять появилась цифра 6,

Поэтому остальные цифры

В левой части повторятся, т.е.

Получим периодическую дробь.

13

6

1

3

0

1

1

1

,

1,

6

0,

2

4

0,

1,

8

6

Ответ: В 2 =1101,(1001) 2

Перевод чисел

А теперь переведем двоичное число в десятичное.

Перевести В2 в D10, если В2=110010,101.

Решение:

D 10 = (1·2 5 +1·2 4 +0·2 3 +0·2 2 +1·2 1 +0·2 0 )+(1·2 -1 +0·2 -2 +1·2 -3 ) =

= (32+16+2)+(0,5+0,125) = 50,625 10

Целая часть

Дробная часть

части

разряды

целая

число

5

4

1

1

3

2

0

0

1

дробная

0

1

0

-1

1

-2

0

-3

1

Задание №1

Вариант 1

А) D 10 →В 2 .

Вариант 2

А) D 10 →В 2 .

• 324
• 122

• 407
• 1 13

Б) В 2 → D 10 .

Б) В 2 → D 10 .

• 1001101
• 10110

• 1010011
• 10011

ДРУГИЕ СИСТЕМЫ СЧИСЛЕНИЯ

D 10

0

B 2

0

O 8

1

H 16

0

2

1

10

0

D 10

1

3

2

4

1

11

8

B 2

100

1000

2

9

O 8

3

5

101

4

6

3

1001

10

10

H 16

110

8

4

1010

11

7

11

5

111

9

1011

12

5

12

6

1100

6

A

7

13

13

1101

14

14

B

7

C

1110

15

15

D

16

1111

E

17

F

ДРУГИЕ СИСТЕМЫ СЧИСЛЕНИЯ

Перевод чисел из одной системы в другую можно через двоичную, пользуясь предыдущей таблицей.

Для этого решим четыре задачи:

• 231 10 → Н 16
• 1110101 2 → О 8
• 465 8 → В 2
• 4А2,3В 16 → О 8

Задача 1. 231 10 → Н 16

231 10 =11100111 2

• Для перевода в шестнадцатеричную систему разобьем целое двоичное число на группы по 4 цифры в каждом, и найдем соответствующие цифры по таблице.

11100111 2 =Е7 16

Задача 2. 1110101 2 → О 8

Для перевода в восьмеричную систему разобьем целое двоичное число на группы по 3 цифры в каждом, и найдем соответствующие цифры по таблице.

001110101 2 =165 8