Практическая работа №3
Тема: «Решение показательных уравнений и неравенств»
Цель: научиться применять свойства показательной функции для решения показательных уравнений и неравенств, закрепить знания и умения по применению методов решения показательных уравнений и неравенств для решения практических задач.
Основные теоретические положения
Определение. Уравнение вида 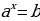 , где
, где 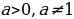 , называется показательным.
, называется показательным.
Если 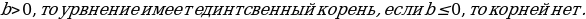
Способы решения показательных уравнений.
Приравнивание показателей.
Суть метода:
1. Уединить слагаемое, содержащее переменную;
2. Привести степени к одному основанию;
3. Приравнять показатели;
4. Решить полученное уравнение;
5. Записать ответ.
Пример:
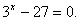
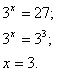
Ответ: x = 3.
Вынесение общего множителя за скобки.
Примечание: выносим за скобки множитель с меньшим показателем.
Пример:
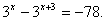

Ответ: x = 1
Введение новой переменной
Как правило, уравнения, решаемые этим способом, сводятся к квадратным.
Пример: 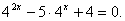
Пусть 4x = а тогда уравнение можно записать в виде:
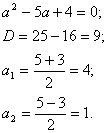
Сделаем обратную замену:
4x = 4 или 4x = 1;
х = 1 или х = 0
Ответ: х = 1 или х = 0
Использование однородности
Определение Показательные уравнения вида 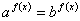 называются однородными.
называются однородными.
Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на 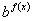 .
.
Пример: 2x = 3x
Разделим обе части уравнения на 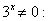
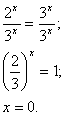
Ответ: x = 0.
Определение. Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.
Решение простейших показательных неравенств.
Простейшими считаются показательные неравенства вида: axy, axay . (ax≤ay, ax≥ay).
Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=ах является возрастающей (а1); eсли же показательная функция у=ах убывает (0), то знак нового неравенства меняют на противоположный:
axay → xy, если a1; знак сохранен, так как функция возрастает;
axay → xy, если 0; функция убывает – знак поменялся;
axay → xy, если a1; знак сохранен, так как функция возрастает
axay → xy, если 0; функция убывает – знак поменялся.
Примеры.
Решить неравенство:
1) 45-2x.
Представим правую часть в виде: 0,25=(25/100)=(1/4)=4-1;
45-2x-1; функция у=4х с основанием 41 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:
5-2x
— 2x
— 2x
x3.
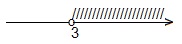
Ответ: (3; +∞).
2) 0,42х+1≥0,16.
Представим число 0,16 в виде степени числа 0,4. Получаем:
0,42х+1≥0,42; основание степеней – число 0,4 — удовлетворяет условию: 0; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:
2х+1≤2;
2 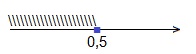 х≤2-1;
х≤2-1;
2х≤1 |:2
x≤0,5.
Ответ: (-∞; 0,5].
Ход работы
| 1 вариант |
| Решите уравнения | Решите неравенства |
| 1) 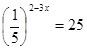 2) 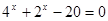 | 6) 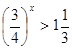 |
| 3) 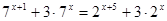 4) 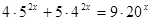 | 7) 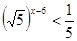 |
| Решите систему уравнений 5) 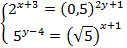 | 8) 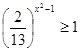 |
| 9) 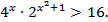 |
|
|
| 2 вариант |
| Решите уравнения | Решите неравенства |
| 1) 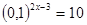 2) 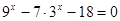 | 6) 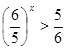 |
| 3) 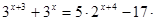 4) 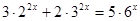 | 7) 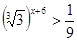 |
| Решите систему уравнений
5) 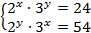 | 8) 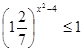 |
| 9) 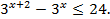 |
|
|
| 3 вариант |
| Решите уравнения | Решите неравенства |
| 1) 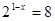 2) 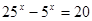 | 6) 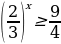 |
| 3) 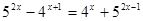 4) 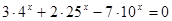 | 7) 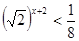 |
| Решите систему уравнений
5) 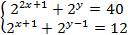 | 8) 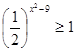 |
| 9) 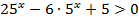 |
|
|
| 4 вариант |
| Решите уравнения | Решите неравенства |
| 1) 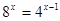 2) 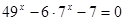 | 6) 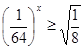 |
| 3) 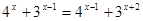 4) 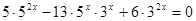 | 7) 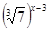 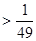 |
| Решите систему уравнений 5) 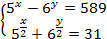 | 8) 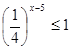 |
| 9) 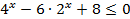 |
|
|
Сделайте вывод по проделанной работе
Контрольные вопросы
От чего зависит возрастание или убывание показательной функции?
Дайте определение показательного неравенства.
Какие условия должны выполняться при решении показательных неравенств?







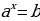 , где
, где 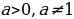 , называется показательным.
, называется показательным.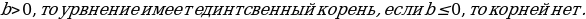
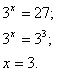

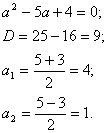
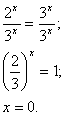
 х≤2-1;
х≤2-1;