Правильные многоугольники

Правильные многоугольники

Работу выполнили ученицы 9 «Б» класса

1

Гимназии им. А. Л. Кекина

Чистова Александра и Стрижич Диана

2019 г

ЗАДАЧИ

1) Ввести понятие правильного

многоугольника.

2) Вывести формулу для

вычисления угла правильного n-

угольника и показать ее

применение в процессе решения

задач.

ИСТРОЧЕСКАЯ СПРВКА

Построение правильного многоугольника с n сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на n равных частей, так как соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник. Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. очку в деле построения правильных многоугольников поставило нахождение построений 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.С тех пор проблема считается полностью решённой.

Понятие правильного многоугольника

Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

Формула для вычисления угла

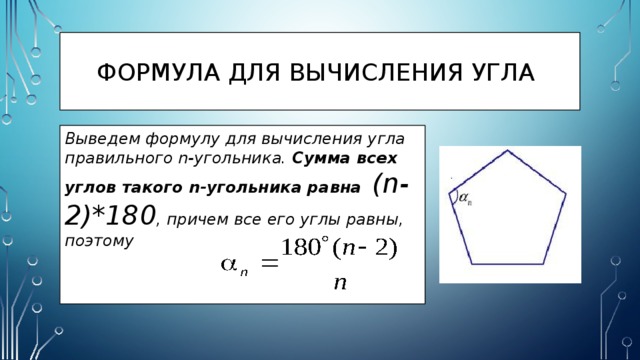
Выведем формулу для вычисления угла правильного n-угольника. Сумма всех углов такого n-угольника равна (n-2)*180 , причем все его углы равны, поэтому

Окружность, описанная около правильного многоугольника

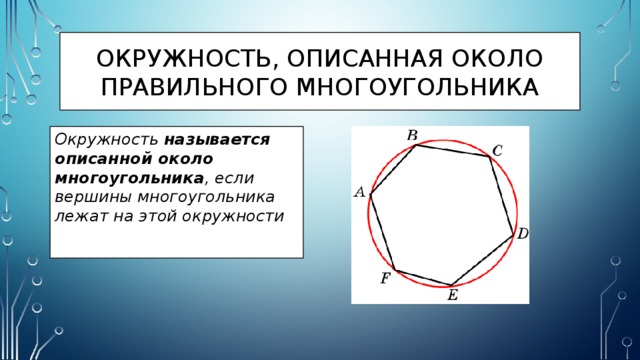
Окружность называется описанной около многоугольника , если вершины многоугольника лежат на этой окружности

Теорема : Около любого правильного многоугольника можно описать окружность, и притом только одну

Окружность, вписанная в правильный многоугольник

Окружность называется вписанной в многоульник , если все стороны многоугольника касаются этой окружности

Теорема : В любой правильный многоугольник можно вписать окружность, и притом только одну

Из этих двух теорем можно сформулировать следующие следствия:

Следствие 1 : Вписанная в правильный многоугольник окружность касается его в серединах его сторон.

Следствие 2 : Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.

Формулы для вычисления

Площадь правильного многоугольника

Сторона правильного многоугольника

Радиус вписанной окружности

Формулы для правильного n -угольника

Задачи на уровень «3»

Задача №1

Дано: Правильный шестиугольник, т.е. n = 6 . Найти: угол правильного шестиугольника

Задачи на уровень «3»

Задача №2

Сторона правильного треугольника равна 4 см. Найдите радиусы вписанной и описанной окружностей

Задачи на уровень «4» и «5»

Задача №1. В правильный шестиугольник ABCDEF, со стороной 6 см, вписан правильный треугольник A1B1C1. Найдите отношение радиуса окружности, вписанной в треугольник A1B1C1, к радиусу окружности, вписанной в шестиугольник ABCDEF.

Задачи на уровень «4» и «5»

Задача №2. Наглядно - поисковая задача. В правильный треугольник MNP вписана окружность. Отрезок NR перпендикулярен отрезку MP и пересекает его в точке K. Угол KMR=300. Найдите радиус вписанной окружности в треугольник MNP и её длину.

Задачи на уровень «4» и «5»

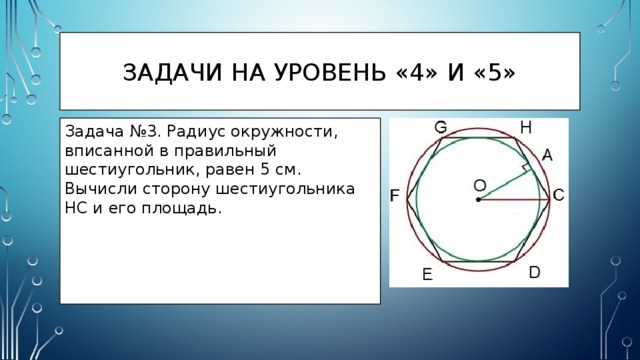
Задача №3. Радиус окружности, вписанной в правильный шестиугольник, равен 5 см.

Вычисли сторону шестиугольника HC и его площадь.

Решение

1. Сторона правильного шестиугольника равна радиусу описанной около него окружности HC=R=OC

CA=53√=53√3 см

r=OA=5 см

HC=2CA

ΔOAC — прямоугольный

HC=103√3 см

∢ ACO=60° (т.к. OC=HC=OH)

2. p=36HC21=3HC; p — полупериметр шестиугольника

tgC=противолежащий катетприлежащий катет=OACA

p=103√ см

tg60°=3√=5CA

S=p⋅rS=103√⋅5

S=503√см2

3√CA=5

Задачи на уровень «4» и «5»

Дан правильный многоугольник и длина радиуса R окружности описанной около многоугольника. Определи площадь многоугольника, если у многоугольника 12 сторон и R=18 см

Решение

1)Так как дан радиус описанной окружности, удобно вычислить площадь маленького треугольника по формуле SAOL=R2⋅sin30°2 и умножить на12.

Также как и первом случае, определим площадь треугольника AOB и умножим её на 10.

S12−уг.=12⋅182⋅sin30°2=972см2

S10−уг.=10⋅182⋅sin36°2=953см2

Ответ: 953 см2

Задачи на уровень «4» и «5»

Дан равносторонний треугольник. Вычисли неизвестные величины, если BO=4дм.

рЕШЕНИЕ

1. Если в равносторонний треугольник вписана окружность, то её центр находится на высоте треугольника и делит высоту в отношении 2:1, считая от вершины треугольника.

tgC=tg60°=3√

Поэтому радиус вписанной окружности равен половине радиуса BO описанной окружности. r=0,5⋅4=2дм

tgC=противолежащий катетприлежащий катет=BEEC

EO=r=2дм

6EC=3√1 (используем основное свойство пропорции)

2. BE=BO+r=4+2=6дм

EC3√=6 (делим обе части уравнения на 3√)

В равностороннем треугольнике высоты равны, поэтому AD=BE=

EC=63√ (умножаем числитель и знаменатель дроби на 3√)

6 дм

EC=263√31=23√дм

3. В равностороннем треугольнике углы равны по 60°. ΔBEC — прямоугольный, т.к. BE — высота.

Задачи на уровень «4» и «5»

Задача 119.

Дано:

Δ ABC - равносторонний,

периметр треугольника

PΔ = 18 см

айти: сторону квадрата, вписанного в ту же окружность

a4 = ?

решение

• Решение:

Т.к. Pn = n • an , то сторона треугольника

18 = 3 • a3 a3 = 6

Тогда радиус описанной окружности

a3 = R• R = = 2

Тогда сторона квадрата a4 = • R = • 2= 2

Ответ: 2.

Задачи по готовым чертежам №1

Решение

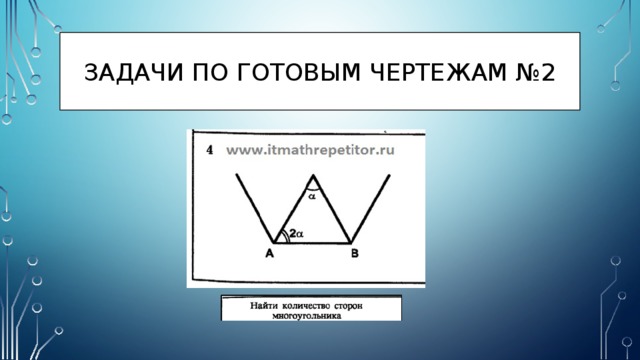
Задачи по готовым чертежам №2

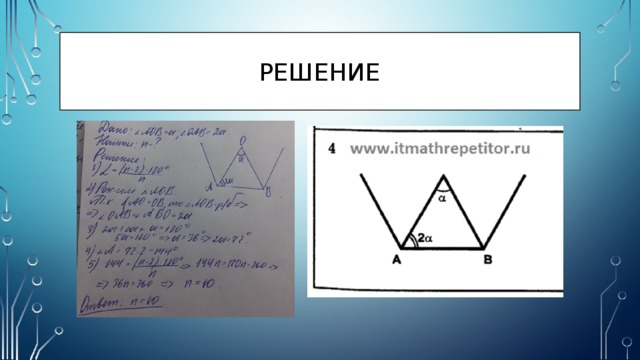
решение

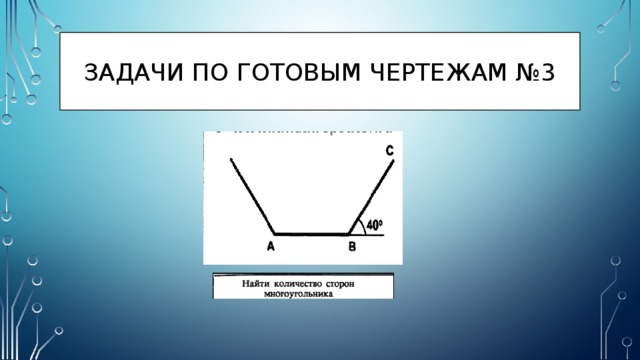
Задачи по готовым чертежам №3

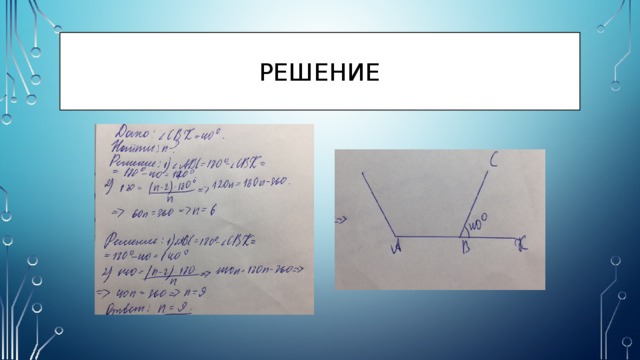
решение

Задачи по готовым чертежам №4

Дано: правильный многоугольник,

дуга AB= 72° ( AB = 72°)

AB - сторона правильного n-угольника

Найти:

количество сторон многоугольника n = ?

решение

Задачи по готовым чертежам №5

Дано:

A1A2A3A4A5 - правильный пятиугольник

αn = • 180° = 108°

решение

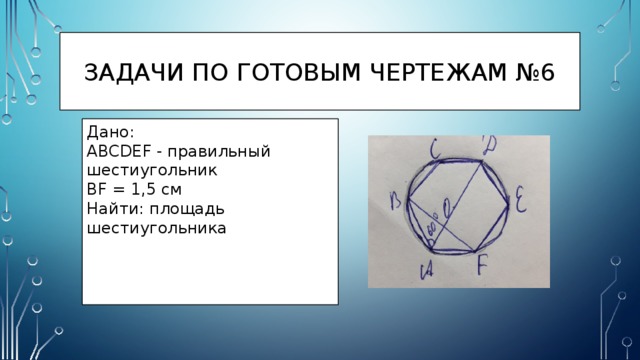
Задачи по готовым чертежам №6

Дано:

ABCDEF - правильный шестиугольник

BF = 1,5 см

Найти: площадь шестиугольника

решение

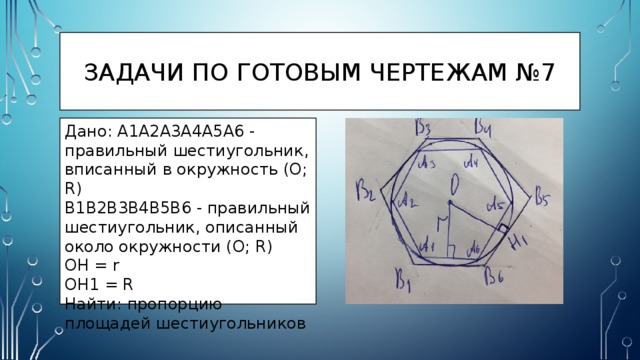
Задачи по готовым чертежам №7

Дано: A1A2A3A4A5A6 - правильный шестиугольник, вписанный в окружность (O; R)

B1B2B3B4B5B6 - правильный шестиугольник, описанный около окружности (O; R)

OH = r

OH1 = R

Найти: пропорцию площадей шестиугольников

Решение

Источники

http://uchitelya.com/geometriya/86735-konspekt-uroka-reshenie-zadach-po-teme-pravilnyy-mnogougolnik-9-klass.html

http://shkolniku.com/algebra/task2503204.html

https://ru.onlinemschool.com/math/formula/regular_polygon/

http://www.treugolniki.ru/pravilnyj-mnogougolnik/

https://dic.academic.ru/dic.nsf/ruwiki/151887