Россия, Оренбург
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 20.01.2020 21:04
Семенов Виктор Анатольевич
преподаватель отдельной дисциплины (математика, информатика и ИКТ)
55 лет
586
88 882 
Местоположение
Специализация
Правило перевода целых десятичных чисел в систему счисления с основанием q.
Категория:
Информатика
13.01.2020 23:16
Просмотр содержимого документа
«Тех_карта»
Просмотр содержимого презентации
«Перевод чисел в q-ичную cc»
Проверка домашнего задания
Задание № 30 .
1000
1111
1000
3333
1000
5555
1000
7777
Задание № 32 .
1
17
3
65
2
54
Проверка домашнего задания
Задание № 35 .
110 2 = 6, 111 2 = 7
77 8 = 63, 100 8 = 64, 101 8 = 65
1В 16 = 27, 1С 16 = 28, 1D 16 = 29, 1E 16 = 30
Задание № 50 .
1/13/20
Правило перевода чисел в сс с основанием q
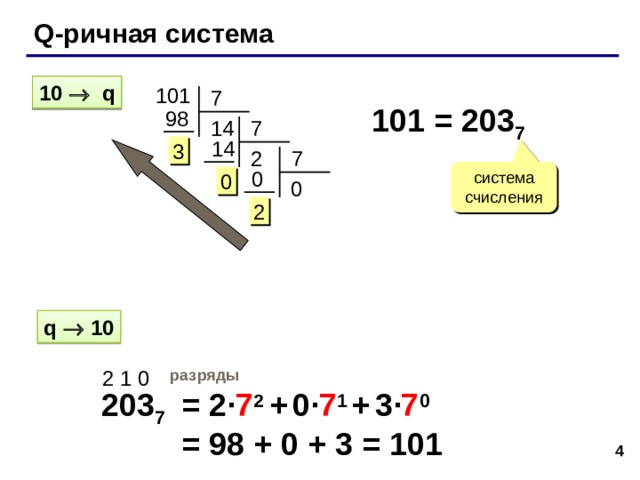
Q-ричная система
10 q
101
7
101 = 203 7
98
7
14
14
3
2
7
0
система счисления
0
0
2
q 10
2 1 0
разряды
203 7
= 2 · 7 2 + 0· 7 1 + 3· 7 0
= 98 + 0 + 3 = 101
Примеры:
406
= 12112 4
X 4
X 7
721
= 2050 7
234
X 3
= 22200 3
580
X 9
= 714 9
393
X 6
= 1453 6
Примеры:
406 7
= 4· 7 2 + 0· 7 1 + 6· 7 0 = 196 + 6 = 202
321 9
= 3· 9 2 + 2· 9 1 + 1· 9 0 = 243+ 18 + 1 = 262
542 6
= 5· 6 2 + 4· 6 1 + 2· 6 0 = 180 +24 + 2 = 206
2120 3
= 2· 3 3 + 1· 3 2 + 2· 3 1 + 0· 3 0 = 54 + 9 + 6 = 69
3233 4
= 3· 4 3 + 2· 4 2 + 3· 4 1 + 3· 4 0 = 192 + 32 + 12 + 3 = 239
Перевод в двоичную и обратно
10
- трудоемко
- 2 действия
8
2
8 = 2 3
Таблица восьмеричных чисел
X 10
X 8
0
1
X 2
0
1
2
000
2
X 10
001
3
3
X 8
4
010
011
X 2
4
5
5
100
6
7
101
6
7
110
111
{
{
{
{
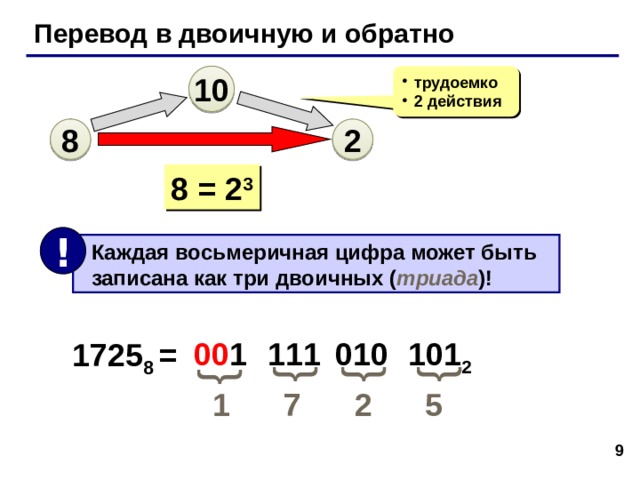
Перевод в двоичную и обратно
10
- трудоемко
- 2 действия
8
2
8 = 2 3
!
Каждая восьмеричная цифра может быть записана как три двоичных ( триада )!
1725 8 =
00 1
111
010
101 2
1 7 2 5
9
Примеры:
3467 8 =
11100110111 2
111011101010 2
7352 8 =
1010011001 2
1231 8 =
9
9
Перевод из двоичной системы
1001011101111 2
Шаг 1 . Разбить на триады, начиная справа:
00 1 001 011 101 111 2
Шаг 2 . Каждую триаду записать одной восьмеричной цифрой:
00 1 001 011 101 111 2
1
3
5
7
1
Ответ: 1001011101111 2 = 11357 8
9
9
Примеры:
5522 8
101101010010 2 =
11111101011 2 =
3753 8
1101011010 2 =
1532 8
9
9
Перевод в двоичную систему
10
- трудоемко
- 2 действия
16
2
16 = 2 4
9
9
Таблица шестнадцатеричных чисел
X 10
0
X 16
X 2
0
1
1
0000
2
X 10
0001
3
2
8
X 16
0010
4
3
X 2
9
8
4
5
0011
1000
9
10
6
5
0100
1001
0101
11
7
A
6
0110
B
12
1010
7
1011
C
0111
13
1100
14
D
E
1101
15
1110
F
1111
9
{
{
{
{
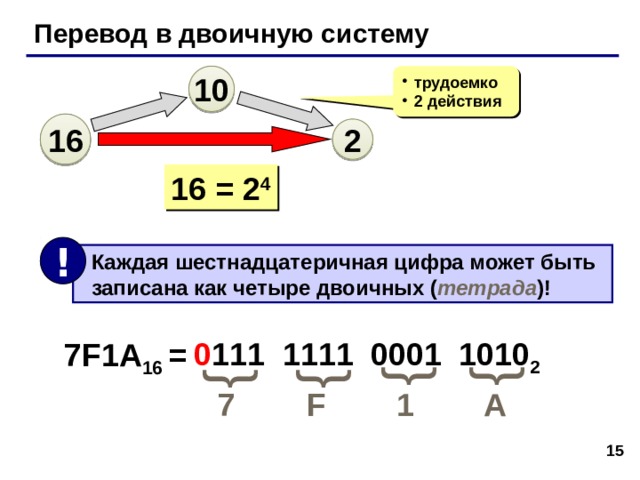
Перевод в двоичную систему
10
- трудоемко
- 2 действия
16
2
16 = 2 4
!
Каждая шестнадцатеричная цифра может быть записана как четыре двоичных ( тетрада )!
7F1A 16 =
0 111
1111
0001
1010 2
7 F 1 A
15
Примеры:
C73B 16 =
1100011100111011 2
10111111100001 2
2FE1 16 =
D4A3 16 =
1101010010100011 2
15
15
Перевод из двоичной системы
1001011101111 2
Шаг 1 . Разбить на тетрады, начиная справа:
000 1 0010 1110 1111 2
Шаг 2 . Каждую тетраду записать одной шестнадцатеричной цифрой:
000 1 0010 1110 1111 2
1
2
E
F
Ответ: 1001011101111 2 = 12EF 16
15
15
Примеры:
AB56 16
1010101101010110 2 =
3CDF5 16
111100110111110101 2 =
110110110101111110 2 =
36D7E 16
15
15
Перевод в восьмеричную и обратно
трудоемко
10
16
8
2
Шаг 1 . Перевести в двоичную систему:
3DEA 16 =
11 1101 1110 1010 2
Шаг 2 . Разбить на триады:
0 11 110 111 101 010 2
Шаг 3 . Триада – одна восьмеричная цифра:
3DEA 16 = 36752 8
15
15
Примеры:
A35 16 =
5065 8
4770 8
9F8 16 =
DB6 16 =
6666 8
765 8 =
1F5 16
723 8 =
1D3 16
753 8 =
1EB 16
15
15
Задачи:
Задача 1: Дано А = A7 16 , B = 251 8 . Найдите сумму A + B. Ответ укажите в двоичной системе.
Ответ: 101010000
Задача 2: Даны 4 целых числа, записанные в двоичной системе:
10001011, 10111000, 10011011, 10110100.
Сколько среди них чисел, больших, чем A4 16 +20 8 .
Ответ: 1
Задача 3: Вычислите: 10101101 2 − 255 8 + D 16 . Ответ запишите в десятичной системе счисления.
Ответ: 13
15
15
Домашнее задание
Устно
§ 1.1.5, стр. 10-12, выучить правило перевода.
Письменно (рабочая тетрадь на печатной основе):
№ 33, 43, 52, 55
15
15
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
