Представление информации в различных системах счисления

Представление информации в различных системах счисления

Системы счисления

Система счисления - совокупность приемов и правил для изображения чисел с помощью символов (цифр), имеющих определенные количественные значения.

Системы счисления делятся на непозиционные и позиционные .

Системы счисления

В непозиционных системах счисления вес цифры (то есть тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.

Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

    Например, в числе 357,6  первый символ  3 означает 3 сотни; второй символ 5 означает 5 десятков, третий символ  7 означает 7 единиц, а четвертый символ  6 означает 6 десятых долей единицы.

Системы счисления

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления - это количество различных символов, используемых для изображения чисел в данной системе счисления.

    В настоящее время, кроме хорошо известной нам десятичной системы счисления, в вычислительной технике используются  двоичная, восьмеричная, и шестнадцатеричная системы счисления. Все применяемые в настоящее время системы счисления позиционные.

Десятичная СС

В десятичной системе счисления для изображения чисел используются 10 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Поэтому основанием десятичной системы счисления является число 10 .

Например: число 123.

3 - три единицы,

2 - два десятка,

1 - одна сотня.

Десятичная СС

Позиция цифры в числе называется разрядом . Разряд числа возрастает справа налево, от младших разрядов к старшим.

Десятичная СС

В развернутой форме записи числа такое умножение записывается в явной форме. так, в развернутой форме запись 123 в десятичной СС будет следующим образом:

2 1 0

123 10 =

1* 10 2 +

2* 10 1 +

3* 10 0

Двоичная СС

В двоичной системе счисления для изображения чисел используется 2 символа: 0,  1 . Поэтому основанием двоичной системы счисления является число 2.

Например, число 5 в двоичной СС в полной форме записывается следующим образом:

5 = 1*2 2 +0*2 1 +1*2 0

В сокращенной и более привычной форме число 5 в двоичной системе записывается так:

5 10 = 101 2

Системы счисления

В восьмеричной системе счисления для изображения чисел используются 8 символов: 0, 1, 2, 3, 4, 5, 6, 7 . Основанием восьмеричной системы счисления является число 8 .

В шестнадцатеричной системе счисления для изображения чисел используются 16 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F , где:

А = 10;   B = 11;  C = 12;  D = 13;  E = 14;  F = 15.

Основанием шестнадцатеричной системы счисления является число 16 .

Перевод чисел из одной СС в другую.

Для преобразования чисел из двоичной, восьмеричной и шестнадцатеричной систем счисления в десятичную необходимо записать число в полной форме и вычислить его значение.

Число представляется в виде суммы произведений ЦИФРЫ на ВЕС РАЗРЯДА.

Вес разряда – это основание СС в степени равной номеру разряда .

Разряды нумеруются от разряда единиц- влево.

Разряд единиц имеет номер 0 .

Перевод из двоичной СС в десятичную

Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа .

Возьмем любое число, например, 1011 2 . Запишем его в полной форме и произведем вычисления:

Т. е число 11 десятичной системы счисления эквивалентно числу 1011 в двоичной системе счисления.

3 2 1 0

1*2 3 +

1011 2 =

1*2 1 +

1*2 0 =

1*8+

0*4+

1*2+

1*1=

0*2 2 +

11 10

Системы счисления

Аналогично происходит перевод чисел из других систем счислений в десятичную.

Пример:

675 8 =? 10

675 8 = 6*8 2 +7*8 1 +5*8 0 = 6*64+7*8+5*1=445 10

2 1 0

Практика

10111 2 =? 10

10111 2 =1*2 4 +0*2 3 +1*2 2 +1*2 1 +1*2 0 =16+0+4+2+1= 23 10

110011 2 =? 10

110011 2 =1*2 5 +1*2 4 +0*2 3 +0*2 2 +1*2 1 +1*2 0 =32+16+0+0+2+1= 51 10

1110011 2 =? 10

1110011 2 =1*2 6 +1*2 5 +1*2 4 +0*2 3 +0*2 2 +0*2 1 +1*2 0 =64+32+16+0+0+2+1= 115 10

26 8 =? 10

26 8 =2*8 1 +6*8 0 =16+6= 22 10

Практика

77 8 =? 10

77 8 =7*8 1 +7*8 0 =56+7= 63 10

1А 16 =? 10

1А 16 =1*16 1 +10*16 0 =16+10= 26 10

ВF 16 =? 10

ВF 16 =11*16 1 +15*16 0 =176+15= 191 10

9C 16 =? 10

9C 16 =9*16 1 +12*16 0 =144+12= 156 10

Перевод чисел из десятичной СС

Перевод чисел из десятичной СС в двоичную, восьмеричную, шестнадцатеричную более сложен. Рассмотрим алгоритм перевода чисел из десятичной СС в двоичную.

Исходное десятичное число многократно (до тех пор, пока частное не станет равным нулю) делится на основание двоичной системы, т.е. на 2. Если при делении образуется остаток, то в соответствующий двоичный разряд записывается 1, если делится без остатка, то записывается 0. Запись остатков в двоичное число ведется слева направо, т.е. от младшего разряда к старшим.

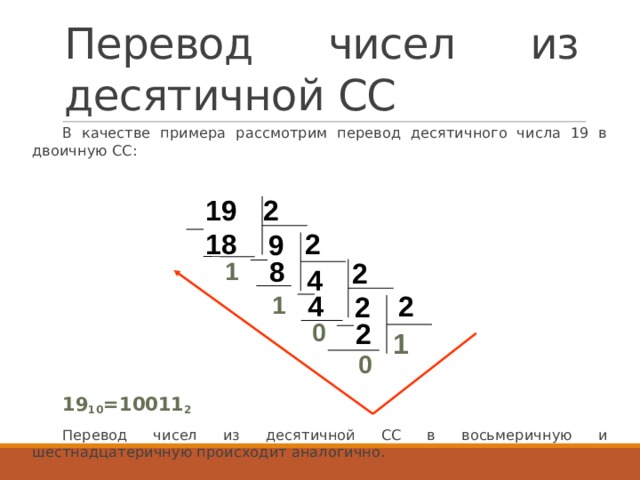
Перевод чисел из десятичной СС

В качестве примера рассмотрим перевод десятичного числа 19 в двоичную СС:

19 10 =10011 2

Перевод чисел из десятичной СС в восьмеричную и шестнадцатеричную происходит аналогично.

19

2

18

2

9

8

1

2

4

4

2

1

2

2

0

1

0

Практика

73 10 =? 2

73 10 =1001001 2

73 10 =? 8

73 10 =111 8

73 10 =? 16

73 10 =49 16

Домашнее задание:

• Выучить термины
• Решить ряд примеров:

• 111010 2 = ? 10 10001111 2 = ? 10 99 10 = ? 2 99 10 = ? 8 99 10 = ? 16
• 111010 2 = ? 10
• 10001111 2 = ? 10
• 99 10 = ? 2
• 99 10 = ? 8
• 99 10 = ? 16