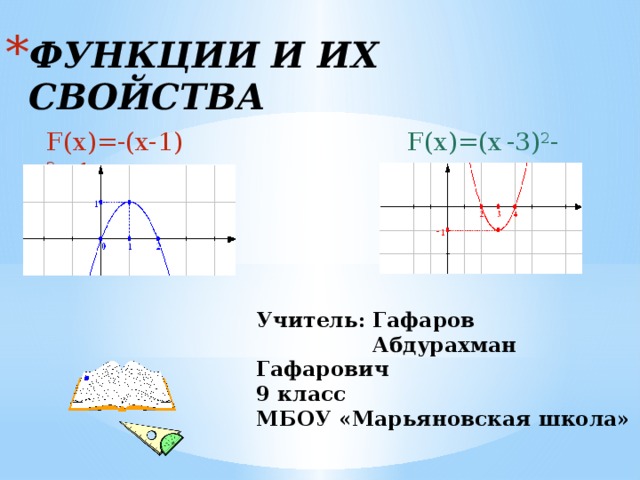
F(x)=-(x-1) 2 +1
F(x)=(x -3) 2 -1
Учитель: Гафаров
Абдурахман Гафарович
9 класс
МБОУ «Марьяновская школа»

- 1. Повторить и систематизировать материал по теме «Функции и их свойства».
- 2. Развивать у учащихся логическое мышление, внимание, формировать потребность приобретении знаний.
- 3. Развивать у учащихся навыки оценивания своих знаний самостоятельно.
- 4. Проверить уровень усвоения изученного материала в условиях диференциации.

- Сегодня на совете директоров должен решится вопрос, какой из присутствующих здесь банков получит кредит доверия на II- четверть в Марьяновской школе. Представляю эти банки:
- Альфа банк- Гура Владимир
- Дельта банк- Котюк Екатерина
- Омега банк- Белянская Виолета

- Активизация знаний учащихся
Линейные:
2) y=x 2 +2
Квадратичные:
3) y=x 2 +9

График какой функции получим, если график функции y=x2 параллельно перенесём:
А) На 4 единицы вниз (y=x²-4)
Б) На 2 единицы вправо (y=((x-2)²)
В) На 3 единицы вверх (y=x²+3)
Г) На 5 единиц влево и 2 единицы вверх (y=(x+5)²+2)
Д) На 1 единицу влево и 3 единицы вверх (y=(x+1)²+3)
Е) На 4 единицы вправо и 2 единицы вниз (y=(x-4)²-2
Ё) На 6 единиц вправо и 3 единицы вниз (y=(x-6)²-3)

Актуализация опорных знаний и умений учащихся
- Определение функции.
- Что такое область определения функции.
- Определение области изменения функции.
- Определение монотонно возрастающей функции.
- Определение монотонно убывающей функции.
- Определение квадратичной функции.
- Что такое максимум функции.
- Что такое минимум функций.
- Определение квадратных уравнений.
- Алгоритм решения квадратных уравнений.

Схема построения графика квадратичной функции y= a x 2 - b x+ c :
- Построить вершину параболы.
- Провести через вершину параболы прямую,
параллельную оси ординат, - ось симметрии
параболы.
- Найти нули функции, если они есть, и построить
на оси абсцисс соответствующие точки параболы.
- Построить дополнительные точки.
- Провести через построенные точки параболу.

- Каждый банк получает задание в виде карточки.
- На обсуждение заданий даётся время 10-15 минут, затем обсуждение прекращается и начинается защита заданий.
- Каждый участник банка принимает участие при защите задания. Представители остальных банков внимательно следят за защитой, и если есть ошибки, они их исправляют.

- Карточка №1
- 1.Алгоритм разложения квадратного трёхчлена на линейные множители. Сократите дробь:
- 2.Схема построения графика функции у= х²-4х+3.
- 3.Постройте график функции у=2(х+1)²-3.

- Алгоритм разложения квадратного трехчлена на линейные множители .
Сократите дробь:
=0 . =0.
D=169-120=49 (7) , D=4 +32=36 (6),
X 1 = = X 1 = ,
X 2 = = . X 2 = .
6(x2-13x+5)=6(x- )*(x-)= 8(8x2-2x-1)=8(x+*(x-
=3(x-5)(2x-1). =(4x+1)*(2x-1).
=
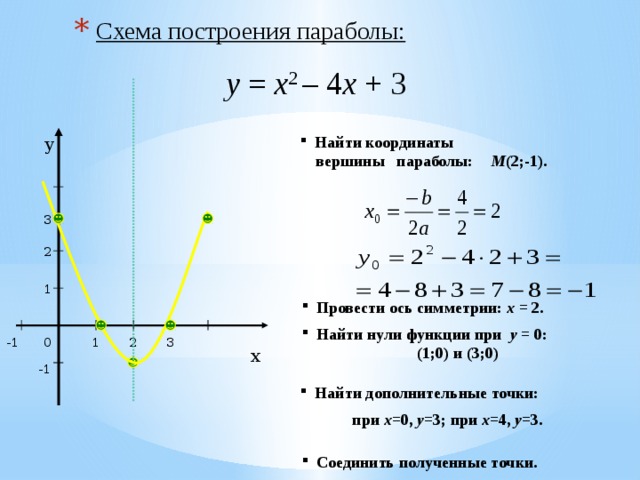
- Схема построения параболы:
у = х 2 – 4 х + 3
вершины параболы: М (2;-1).
у
3
2
1
- Провести ось симметрии: х = 2.
- Найти нули функции при у = 0:
(1;0) и (3;0)
0
1
2
-1
3
х
-1
- Найти дополнительные точки:
при х =0, у =3; при х =4, у =3.
- Соединить полученные точки.
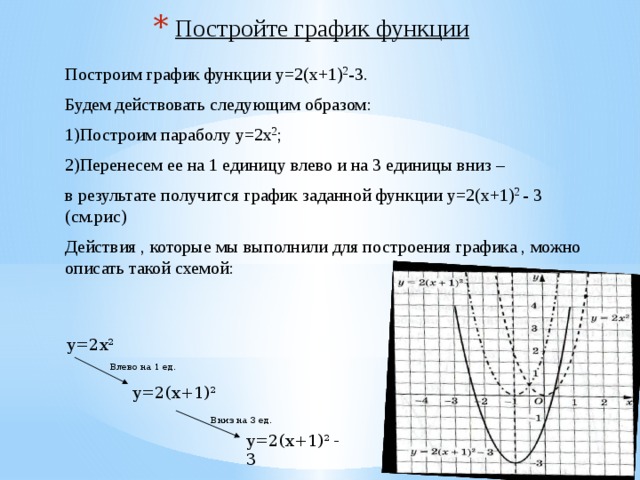
Построим график функции y=2(x+1) 2 -3.
Будем действовать следующим образом:
1)Построим параболу y=2x 2 ;
2)Перенесем ее на 1 единицу влево и на 3 единицы вниз –
в результате получится график заданной функции y=2(x+1) 2 - 3 (см.рис)
Действия , которые мы выполнили для построения графика , можно описать такой схемой:
y=2x 2
Влево на 1 ед.
y=2(x+1) 2
Вниз на 3 ед.
y=2(x+1) 2 - 3

Карточка №2
- 1. Функция y=ax², её свойства и график.
- 2. Исследуйте график функции y=3x²+12x+9.
- 3. Постройте график функции y=-2(x+3)²+2.
 0 1 2 -2 0 -2 2 0 1 х х 2 Построим график функции y=-2x 2 а‹0 x -3 y = 2 x 2 -2 -18 -1 -8 0 -2 1 0 2 -2 3 -8 -18 у=-2х 2 " width="640"
0 1 2 -2 0 -2 2 0 1 х х 2 Построим график функции y=-2x 2 а‹0 x -3 y = 2 x 2 -2 -18 -1 -8 0 -2 1 0 2 -2 3 -8 -18 у=-2х 2 " width="640"
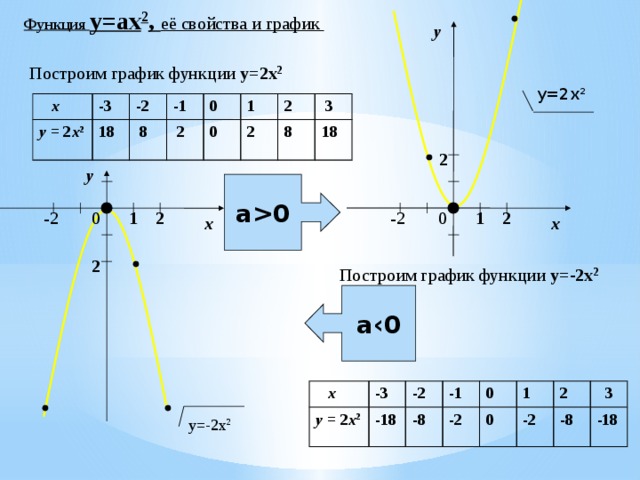
Функция y=ax 2 , её свойства и график
у
Построим график функции y=2x 2
у=2х 2
x
y = 2 x 2
-3
-2
18
-1
8
0
2
1
0
2
2
8
3
18
2
у
а0
1
2
-2
0
-2
2
0
1
х
х
2
Построим график функции y=-2x 2
а‹0
x
-3
y = 2 x 2
-2
-18
-1
-8
0
-2
1
0
2
-2
3
-8
-18
у=-2х 2
 0. M(x 0 ;y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3. M(-2;3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 +4x+3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -1 -2 -3 1 0 x -3 x y 0 -1 9 0 " width="640"
0. M(x 0 ;y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3. M(-2;3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 +4x+3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -1 -2 -3 1 0 x -3 x y 0 -1 9 0 " width="640"
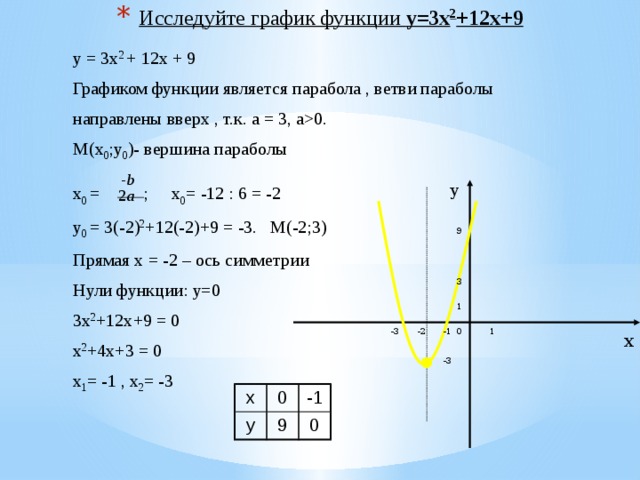
- Исследуйте график функции y=3x 2 +12x+9
y = 3x 2 + 12x + 9
Графиком функции является парабола , ветви параболы
направлены вверх , т.к. а = 3, a0.
M(x 0 ;y 0 )- вершина параболы
x 0 = ; x 0 = -12 : 6 = -2
y 0 = 3(-2) 2 +12(-2)+9 = -3. M(-2;3)
Прямая х = -2 – ось симметрии
Нули функции: y=0
3x 2 +12x+9 = 0
x 2 +4x+3 = 0
x 1 = -1 , x 2 = -3
2 а
- b
у
9
3
1
-1
-2
-3
1
0
x
-3
x
y
0
-1
9
0
m = -3
n = 2
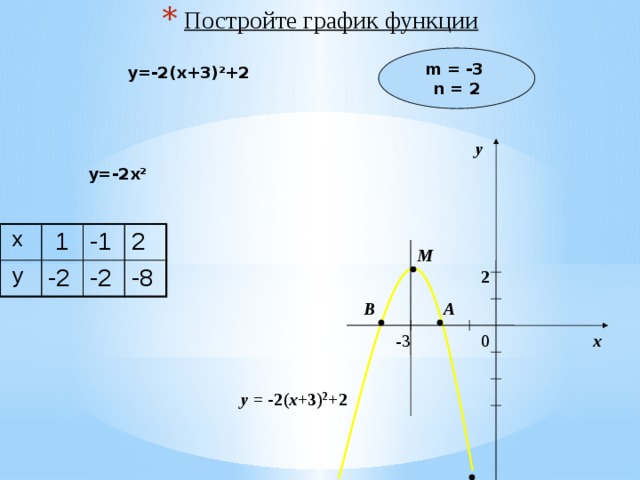
y=-2(x+3) 2 +2
у
у=-2х 2
х
1
у
-1
-2
2
-2
-8
М
2
А
В
-3
х
0
у = -2( x +3) 2 +2

Карточка №3
- Общая схема исследования квадратичной функции
Ответ:
1. Найти область определения и значения функции.
2. Выяснить, является ли функция четной.
3. Вычислить координаты точек пересечения графика с осями координат.
4. Найти промежутки знакопостоянства функции.
5.Найти промежутки возрастания и убывания функции.
6. Найти точки экстремума, экстремумы функции.
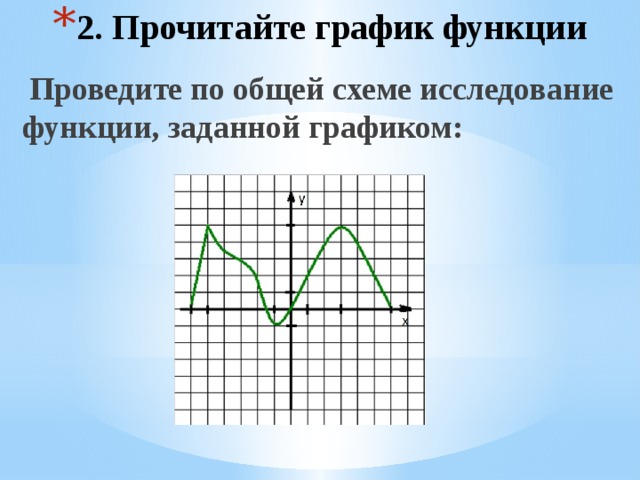
- 2. Прочитайте график функции
Проведите по общей схеме исследование функции, заданной графиком:
 0: (-6;-1,5) U (0;6). f(x) 4.Нули функции: -6; -1,5; 0; 6. Функция возрастает: [-6;5] U [-1;3]. Функция убывает: [-5; -1] U [3;6]. 5.Наибольшие и наименьшие значения функции: min f(x)=-1 max f(x)=5. " width="640"
0: (-6;-1,5) U (0;6). f(x) 4.Нули функции: -6; -1,5; 0; 6. Функция возрастает: [-6;5] U [-1;3]. Функция убывает: [-5; -1] U [3;6]. 5.Наибольшие и наименьшие значения функции: min f(x)=-1 max f(x)=5. " width="640"
- 1.D(х)=[-6;6]. 2.Е(у)=[-1;5].
- 2.Функция не является ни чётной, ни нечётной.
- 3.Промежутки знакопостоянства.
- f(x)0: (-6;-1,5) U (0;6).
- f(x)
- 4.Нули функции: -6; -1,5; 0; 6.
- Функция возрастает: [-6;5] U [-1;3].
- Функция убывает: [-5; -1] U [3;6].
- 5.Наибольшие и наименьшие значения функции:
- min f(x)=-1 max f(x)=5.
 0 2) g Данный график получается смещением параболы у = ах² по оси Оу на g единиц вверх (если g 0) или вниз (если g " width="640"
0 2) g Данный график получается смещением параболы у = ах² по оси Оу на g единиц вверх (если g 0) или вниз (если g " width="640"
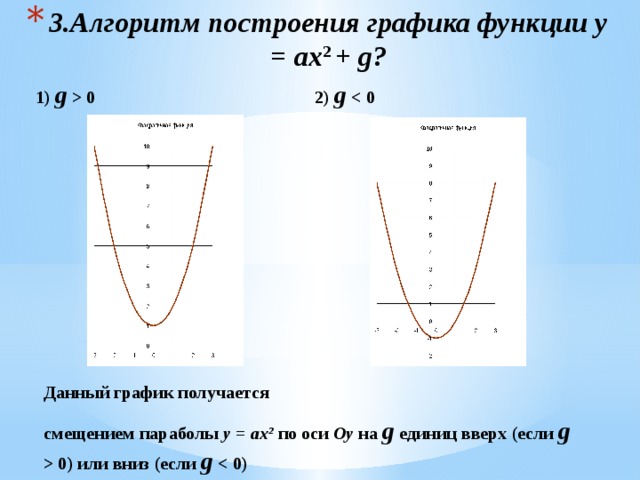
- 3.Алгоритм построения графика функции у = ах 2 + g?
1) g 0 2) g
Данный график получается
смещением параболы у = ах² по оси Оу на g единиц вверх (если g 0) или вниз (если g

Сегодня на уроке:
- я научился…
- я узнал(а)…
- расширил(а) представления о…
- мне было трудно…
- мне было особенно интересно…
- я остался доволен…
- какими приемами сегодня на уроке мы пользовались?

Спасибо за урок!



















 0 1 2 -2 0 -2 2 0 1 х х 2 Построим график функции y=-2x 2 а‹0 x -3 y = 2 x 2 -2 -18 -1 -8 0 -2 1 0 2 -2 3 -8 -18 у=-2х 2 " width="640"
0 1 2 -2 0 -2 2 0 1 х х 2 Построим график функции y=-2x 2 а‹0 x -3 y = 2 x 2 -2 -18 -1 -8 0 -2 1 0 2 -2 3 -8 -18 у=-2х 2 " width="640"
 0. M(x 0 ;y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3. M(-2;3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 +4x+3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -1 -2 -3 1 0 x -3 x y 0 -1 9 0 " width="640"
0. M(x 0 ;y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3. M(-2;3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 +4x+3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -1 -2 -3 1 0 x -3 x y 0 -1 9 0 " width="640"



 0: (-6;-1,5) U (0;6). f(x) 4.Нули функции: -6; -1,5; 0; 6. Функция возрастает: [-6;5] U [-1;3]. Функция убывает: [-5; -1] U [3;6]. 5.Наибольшие и наименьшие значения функции: min f(x)=-1 max f(x)=5. " width="640"
0: (-6;-1,5) U (0;6). f(x) 4.Нули функции: -6; -1,5; 0; 6. Функция возрастает: [-6;5] U [-1;3]. Функция убывает: [-5; -1] U [3;6]. 5.Наибольшие и наименьшие значения функции: min f(x)=-1 max f(x)=5. " width="640"
 0 2) g Данный график получается смещением параболы у = ах² по оси Оу на g единиц вверх (если g 0) или вниз (если g " width="640"
0 2) g Данный график получается смещением параболы у = ах² по оси Оу на g единиц вверх (если g 0) или вниз (если g " width="640"





















