Презентация к уроку "Общие методы решения уравнений" в 11 классе

• Общие методы решения уравнений

«Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, что, следуя нашему методу, мы достигли цели».

Готфрид Лейбниц

01.07.1646 – 14.11.1716 гг.

• Назовите виды уравнений:

• Что называют решением уравнения?

• Что значит – решить уравнение?

- Что называют областью допустимых значений переменной (ОДЗ)?

Найдите ОДЗ уравнения

2.

3.

4.

6.

7.

8.

9.

10. =

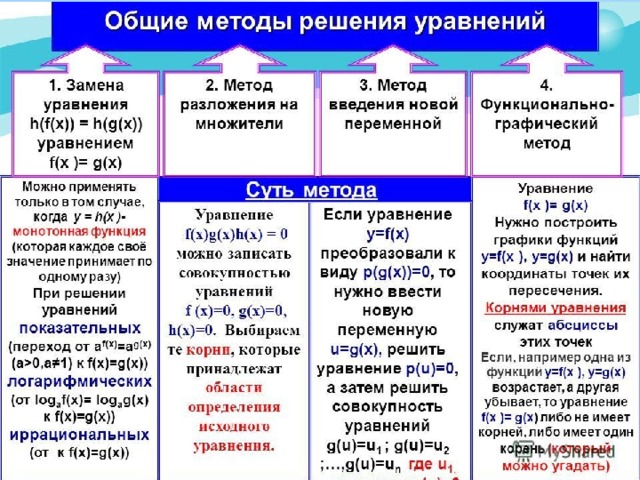
Методы решения уравнений – это способы, приёмы, с помощью которых можно решить то или иное уравнение.

Общие методы решения уравнений – это такие способы, приёмы, с помощью которых можно решить  уравнения разного типа.

Функционально-графический метод

Метод разложения на множители

Общие методы решения уравнений

Метод введения новой переменной

Замена уравнения

h=h

Уравнением f=g

Метод замены уравнения h(f(х)) = h(g(х)) уравнением f(х) = g(х)

- Когда применяется этот метод? - Когда нельзя применять этот метод?

Если функция h(х) монотонная , то она принимает каждое своё значение только один раз .

Метод разложения на множители

- В чем заключается суть данного метода? - Как правильно отобрать корни?

f(x) g(x) h(x) = 0 заменяют совокупностью уравнений f(x) = 0 , g(x) = 0 , h(x) = 0 .

Метод введения новой переменной

- В чем заключается суть данного метода? - На что важно обратить внимание, если мы ввели новую переменную?

Функционально-графический метод решения уравнения f(х) = g(х)

- В чем заключается идея данного метода?

С троят графики функций у = f(х) и у = g(х) .

Затем находят точки пересечения этих графиков, определяют их абсциссы.

1. Определите метод решения уравнения:

а) x 3 – 9 x 2 + 20 х = 0

2. Решите уравнение:

5. Работа в парах ( 6 уравнений)

1 пара:

2 пара:

3пара:

4 пара:

5 пара:

6 пара:

Ответы:

1 пара

1 пара

Ответы:

8; 22.

2 пара

8; 22.

2 пара

3 пара

3 пара

4 пара

4 пара

10;

5;

5 пара

5 пара

6 пара

6 пара

1

1

1

1

Метод мажорант

Метод мажорант  основан на том, что множество значений некоторых функций ограничено. При использовании  метода мажорант  мы выявляем точки ограниченности функции, то есть в каких пределах изменяется данная функция,  а затем используем эту информацию для решения уравнения или неравенства.

Пусть f ( x ) и g ( x ) – некоторые функции, определённые на множестве D. Пусть f ( x ) ограничена на этом множестве числом А сверху, а g ( x ) ограничена на этом множестве тем же числом А , но снизу.

Тогда уравнение f ( x ) = g ( x ) равносильно системе:

Самостоятельная работа

Вариант№1

а)

№ задания

1

Ответ

А)

2

В)

3

4

В)

5

б)

Г)

6

В)

Б)

В)

Вариант№2

№ задания

а)

1

Ответ

2

В)

3

Б)

4

Г)

5

б)

6

В)

В

А)

Б)

Вариант№3

а)

№ задания

Ответ

1

2

А)

3

В)

4

В)

б)

5

В)

6

Г)

Г)

Б)

Вариант№4

№ задания

а)

Ответ

1

В)

2

3

Б)

4

Г)

б)

5

В)

В)

6

А)

А)