Презентация к уроку "Площадь трапеции"

• Там, где с морем сливается Нил, В древнем жарком краю пирамид Математик греческий жил – Многознающий, мудрый Евклид. Геометрию он изучал, геометрии он обучал. Написал он великий труд. Эту книгу «Начала» зовут.

13.12.19

Свойство площадей равных фигур

• Равные многоугольники имеют равные площади

Свойство площадей

• Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

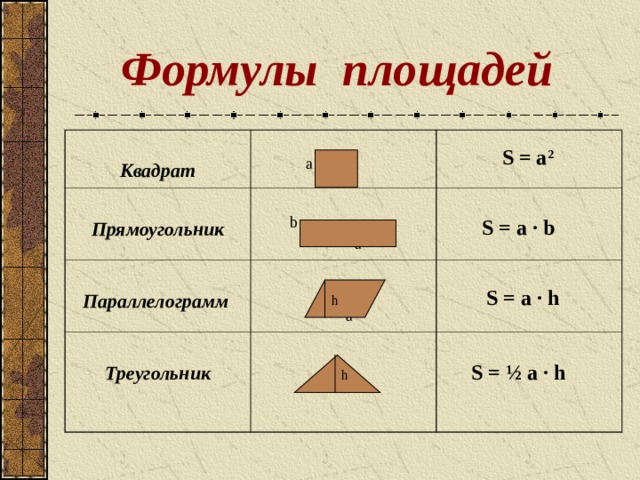
Формулы площадей

Квадрат

а

Прямоугольник

b

a

Параллелограмм

a

Треугольник

a

S = a 2

S = a · b

S = a · h

h

h

S = ½ a · h

• Еще 4-5 тыс.лет назад вавилоняне умели определять площадь трапеции в квадратных единицах.
• Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы: сумма параллельных сторон делилась пополам и умножалась на высоту.

13.12.19

Определение площадей геометрических фигур - одна из древнейших практических задач . Правильный подход к их решению был найден не сразу . Один из самых простых и доступных способов вычисления площадей был открыт Евклидом. При вычислении площадей он использовал простой прием , называемый методом разбиения .

13.12.19

Вычисление площадей на Руси

Потребность измерения площадей привела к созданию на Руси рукописей геометрического содержания чисто практического характера в XVI веке.

В рукописи «Книга сошного письма» собраны правила измерения площадей. Трапеция: площадь трапеции выражается произведением полусуммы оснований на «хобот», т.е. на боковую сторону, что тоже неверно.

Вопреки сохранившимся рукописям создание «русскими мастерами каменных дел» различных сооружений кремлевских стен и башен, храмов говорит о том, что эти мастера обладали знаниями в области геометрии. Без таких знаний в 1560 году не было бы и храма Василия Блаженного в Москве.

13.12.19

• Что называется трапецией?
• Что такое основания трапеции?
• Как называют две другие стороны?
• Какие виды трапеций знаете?

« Трапеция » - слово греческое, означающее в древности «столик». Отсюда идет название трапеза, трапезная. В «Началах» Евклида ( III в.до н.э.) трапеция – любой четырехугольник (не параллелограмм). Трапеция в нашем смысле встречается впервые у древнегреческого математика Пасидона. Только в XVIII веке это слово приобретает современный смысл.

Четыре яркие звезды созвездия α, β, γ и δ располагаются в вершинах трапеции – туловища льва. А голову льва образуют звезды, располагающиеся в виде серпа. Поэтому этот астеризм и называется «серп».

B

8 см

C

H

6см

30º

A

D

K

Решение :

трапеция ABCD состоит из 2 Δ : Δ ABD и Δ BCD

Чтобы найти её площадь надо найти площади этих треугольников.

Проведём высоту BK в Δ ABD

и DH в Δ BCD ;

S ABD = ½ AD  BK

S ABCD = S ABD + S BCD

S BCD = ½ BC  DH

S ABCD = ½ AD  BK + ½ BC  DH

= ½  BK  (AD+BC)

S ABCD = ½ BK  (AD+BC)

BK - высота, AD,BC - основания

Теорема : Площадь трапеции равна произведению полусуммы её оснований на высоту

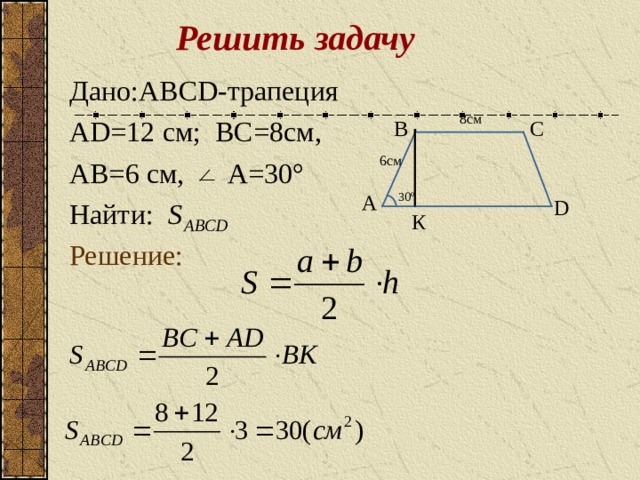
Решить задачу

Дано: ABCD -трапеция

AD=12 см; BC=8 см,

AB=6 см, A=30°

Найти:

Решение:

8 см

C

B

6см

30º

A

D

К

13

• Дайте определение высоты трапеции:

а) Назовите высоту у прямоугольной трапеции.

б) Сколько высот можно построить для трапеции?

Что о них можно сказать?

13

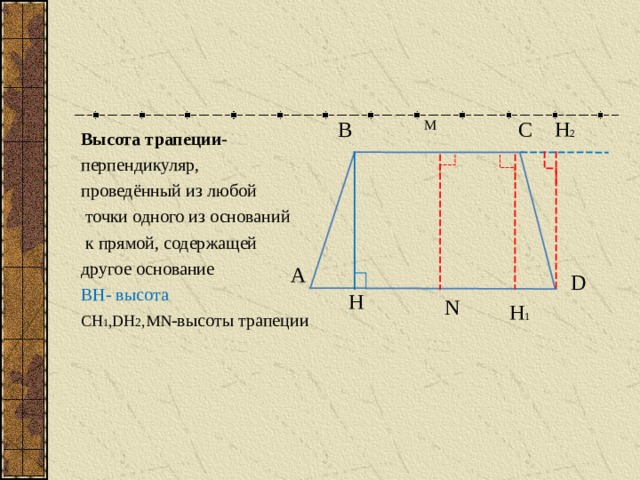
M

H 2

C

B

Высота трапеции -

перпендикуляр,

проведённый из любой

точки одного из оснований

к прямой, содержащей

другое основание

BH - высота

CH 1 ,DH 2 ,MN -высоты трапеции

A

D

H

N

H 1

13

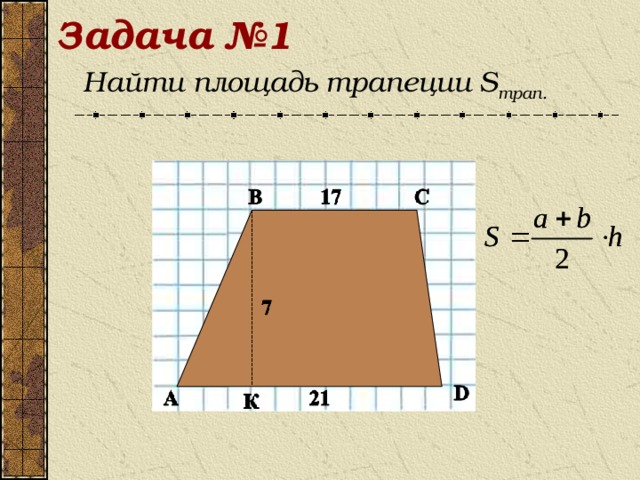
Задача №1

Найти площадь трапеции S трап.

Задача №2

Найти площадь трапеции S трап.

C

B 2

8

30 º

D

К

A 16

Задача №3

Найти площадь трапеции S трап.

B

C

К

12

D

A Е

ED=18

Задача №4

Найти площадь трапеции S трап.

AD=15

B

C

7

12

30 º

A H

D

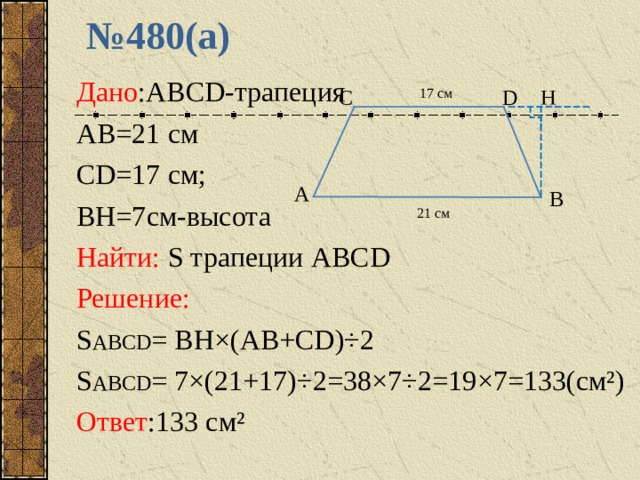
№ 480(а)

Дано : ABCD -трапеция

AB=21 см

CD=17 см;

BH=7 см - высота

Найти: S трапеции ABCD

Решение:

S ABCD = BH×(AB+CD)÷2

S ABCD = 7×(21+17)÷2 = 38×7÷ 2= 19×7=13 3(см²)

Ответ :133 см²

H

17 см

D

C

A

B

21 см

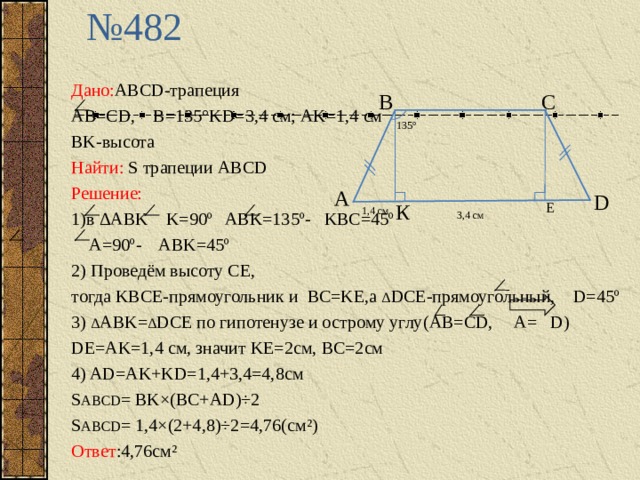
№ 482

Дано: ABCD -трапеция

AB=CD , B= 1 3 5 °KD=3,4 см; AK=1,4 см

BK- высота

Найти: S трапеции ABCD

Решение:

1) в Δ ABK K=90º ABK=135º- KBC=45º

A=90º- ABK=45º

2) Проведём высоту С E ,

тогда KBCE- прямоугольник и BC=KE, а Δ DCE -прямоугольный, D=45º

3) Δ ABK= Δ DCE по гипотенузе и острому углу( AB=CD, A= D )

DE=AK=1,4 см, значит KE=2 см, BC=2 см

4) AD=AK+KD=1,4+3,4=4,8 см

S ABCD = BK×(BC+AD)÷2

S ABCD = 1,4×(2+4,8)÷2 = 4,76 (см²)

Ответ : 4,76 см²

C

B

135°

A

D

E

К

1,4 см

3,4 см

Подведем итог:

• На уроке вывели формулу трапеции. Она имеет вид:

S трап =

2. Научились применять эту формулу для решения задач.

22

• П. 53
• № 480(б,в)
• № 481

22

Желаю успеха!

«К большому

терпению

придет

и уменье.»