Презентация к уроку "Уравнения. Общие методы решения уравнений"

«Уравнения. Общие методы решения уравнений»

Цель :

• Обобщить теоретические знания по теме «Общие методы решения уравнений».
• Рассмотреть решения заданий базового и повышенного уровня сложности.

Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, что, следуя нашему методу, мы достигли цели.

Готфрид Лейбниц

Теоретические знания:

1. Что называют корнем уравнения?

• (называют то значение переменной, при котором данное уравнение обращается в верное равенство.)

2. Что значит – решить уравнение?

• (это значит найти все его корни или доказать, что корней нет.)

3. Что называют областью допустимых значений переменной (ОДЗ)?

• ( Областью определения уравнения f(x)=g(x) или ОДЗ называют множество тех значений переменной х, при которых одновременно имеют смысл выражения f(x) и g(x))

4. Какие уравнения являются равносильными?

• (Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называют равносильными, если множества их корней совпадают)

5. Какие преобразования приводят к равносильным уравнениям?

• (Прибавление к обеим частям уравнения одного и того же числа, умножение обеих частей уравнения на одно и то же число, деление обеих частей уравнения на одно и то же число не равное нулю.)

6. Какие действия при преобразовании уравнений можно назвать «опасными» и почему?

7. Укажите ОДЗ уравнений:

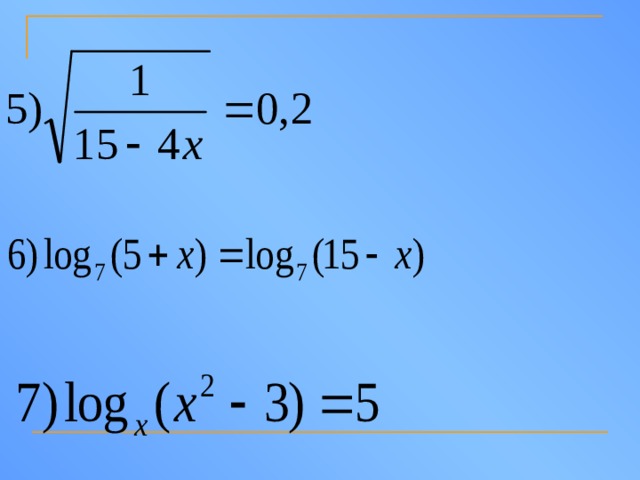
Ответы:

8. Виды уравнений.

9.Основные методы решения уравнений.

1 метод Замена

уравнени я

уравнением

При решении показательных уравнений

(а  0, а≠1)

При решении логарифмических уравнений

При решении иррациональных уравнений

Этот метод можно применять только тогда, когда y=h(x) – монотонная функция

Пример

=

ОДЗ:

-х=15-3х

+2х-15=0

Х=-5 х=3

ОДЗ удовлетворяют все корни

Ответ: -5;3.

0

1

5

Можно ли применить этот метод при решении уравнений:

=

=

НЕТ

НЕТ

у=- немонотонная функция.

у=- немонотонная функция.

Потеря корня (х=1)

Потеря бесконечного множества корней.

2 метод Разложения на множители

Уравнение

заменить

совокупностью уравнений

Необходима проверка корней

Пример :

ОДЗ:

С учётом ОДЗ:

Ответ:

3 метод Введения новой переменной

Уравнение

преобразуем к виду:

вводим новую переменную:

решаем совокупность уравнений

Пример :

не удовлетворяет

Ответ:

4 метод Функционально - графический

для решения уравнения

строим графики функций

ПРИМЕР 1. Решить уравнение

Решение.

1)

2) А(1;1), В(4;2)

3) х 1 =1 ; х 2 = 4 .

Ответ: 1; 4.

ПРИМЕР 2. Решить уравнение

Решение.

1) Подбором находим корень х = 2 .

3)

Ответ: 2.

Значит, х = 2 – единственный корень.

Определить метод решения уравнений.

Замена

Введение новой переменной

Разложение на множители

Функционально-графический

Введение новой переменной

«Держать в голове»

При решении уравнения каждый раз выделять три этапа:

1. Технический.

2. Анализ.

3. Проверка (Необязательно. Но если анализ показал , что проверка обязательна, а вы ее не сделали, то уравнение не может считаться решенным верно).

Физминутка

Рефлексия (итог урока)

• Какую цель ставили перед собой на уроке?
• Cмогли ли её достичь?
• Оцените свою деятельность на уроке.
• Какой вид деятельности вам больше понравился?