Презентация по Теме "Призма"

КГБ ПОУ «Чугуевский колледж сельского

хозяйства и сервиса»

«ПРИЗМА»

Усова Ирина Александровна

преподаватель

Призма - это многогранник, состоящий из двух плоских многоугольников, лежащих в разных параллельных плоскостях и всех отрезков, соединяющих соответствующие точки этих многоугольников.

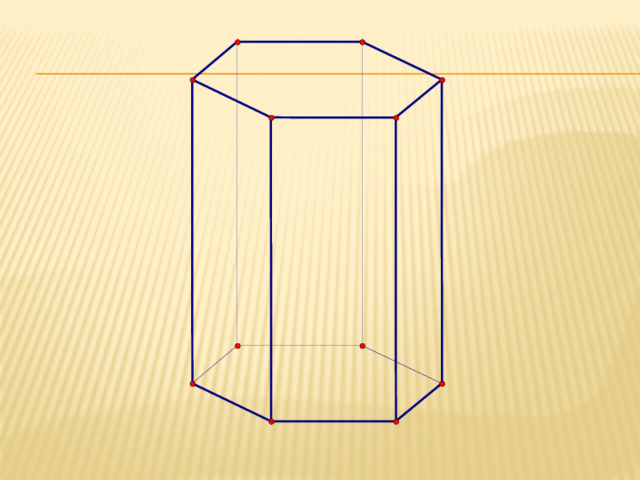
Элементы призмы

Верхнее основание

вершина

Боковое ребро

Боковая грань

Нижнее основание

высота

Элементы призмы

• Основания – это грани, совмещаемые параллельным переносом.
• Боковая грань – это грань, не являющаяся основанием.
• Боковые рёбра – это отрезки, соединяющие соответствующие вершины оснований.
• Вершины – это точки, являющиеся вершинами оснований.
• Высота – это перпендикуляр, опущенный из одного основания на другое.
• Диагональ – это отрезок, соединяющий две вершины, не лежащие в одной грани.

призма

прямая

наклонная

правильная

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой , в противном случае – наклонной .

Прямая призма называется правильной , если в её основании лежит правильный многоугольник

Правильная призма

Четырехугольная

Шестиугольная Треугольная

призма призма призма

Диагональные сечения параллелепипеда

Площадь боковой поверхности призмы

Теорема о площади боковой поверхности прямой призмы

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы

P - периметр

h – высота призмы

Площадь полной поверхности призмы

Площадью полной поверхности призмы называется сумма площадей всех ее граней.

Призмы встречающиеся в жизни

Здание под шпилем, Барнаул

Здание вокзала, Барнаул

Александрийский маяк

Задача № 229 (б), стр.68

В правильной n-угольной призме сторона основания равна а и высота равна h . Вычислите площади боковой и полной поверхности призмы, если: n = 4, а = 12 дм, h = 8 дм.

Дано: n = 4

а = 12 дм

h = 8 дм

Найти:

Sбок – ?

Sпол – ?

взаимопроверка

РЕШЕНИЕ:

Т.К. n = 4, то призма четырехугольная .

Sбок = = 4 а h

Sбок = 4 · 8 · 12 = 384 (дм 2 )

Sпол = 2Sосн + Sбок

Sосн = а 2 = 12 2 = 144 (дм 2 )

Sпол= 2 · 144 + 384 = 672 (дм 2 )

Ответ: 384 дм 2 , 672 дм 2

Сверяем ответ

РЕШЕНИЕ:

Т.К. n = 6, то призма шестиугольная.

Sбок = 6 · 50 · 23 = 6900 (см2) = 69 (дм 2 )

Sпол = 3 а · (2h + √3 · а )

Sпол = 69 · (100 + 23√3) = 69 · 140 = 9660 (см 2 ) = 97 (дм 2 )

Ответ: 69 дм 2 , 97 дм 2

Герон Александрийский

Фо́рмула Геро́на

Древнегреческий ученый, математик,

физик, механик, изобретатель.

позволяет вычислить

площадь треугольника ( S )

Математические работы Герона

по его сторонам a, b, c :

являются энциклопедией античной

прикладной математики. В лучшей из

них- "Метрике" - даны правила и

формулы для точного и приближенного

вычисления площадей правильных

где р — полупериметр треугольника:

многоугольников, объемов усеченных

конуса и пирамиды, приводится

формула Герона для определения

площади треугольника по трем сторонам,

даются правила численного решения

квадратных уравнений и приближенного

извлечения квадратного и кубического

корней .

неизвестно,

вероятно

I в .

Решить задачу

• В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы равна 18 см. Найдите площадь полной поверхности и объём призмы.

Сверяем ответ

РЕШЕНИЕ:

Р = 10+17 +21 = 48(см)

Sбок = 48· 18 = 864 (см 2 )

Sосн =

= 84(см 2 )

Sосн =

Sпол = 864 + 168 = 1032 (см 2 )

V= S осн ∙h = 84 ·18 = 1512 (см 3 )

Ответ:

1032 (см 2 )

, 1512 (см 3 )

Продолжите фразу:

• “ Сегодня на уроке я узнал…”
• “ Сегодня на уроке я научился…”
• “ Сегодня на уроке я познакомился…”
• “ Сегодня на уроке я повторил…”
• “ Сегодня на уроке я закрепил…”