Презентация по теме "Теорема о трёх перпендикулярах"

Тема урока

Теорема о трёх перпендикулярах.

• festival.1september.ru
• Учительский портал
• www.cleverstudents.ru

Рассмотреть теорему

«О трёх перпендикулярах» и научиться применять её при решении задач.

• Перпендикуляр
• Наклонная
• Проекция
• Точка - вершина
• Прямая – ребро
• Плоскость – грань

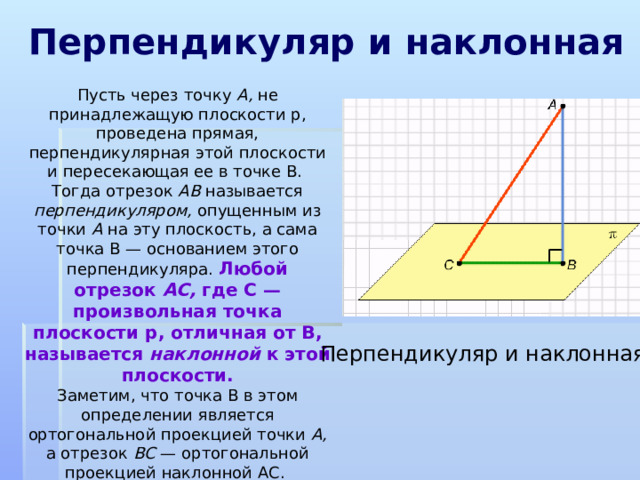
Перпендикуляр и наклонная

Пусть через точку А, не принадлежащую плоскости p , проведена прямая, перпендикулярная этой плоскости и пересекающая ее в точке В.

Тогда отрезок АВ называется перпендикуляром, опущенным из точки А на эту плоскость, а сама точка В — основанием этого перпендикуляра. Любой отрезок АС, где С — произвольная точка плоскости p , отличная от В, называется наклонной к этой плоскости.

Заметим, что точка В в этом определении является ортогональной проекцией точки А, а отрезок ВС — ортогональной проекцией наклонной A С.

Перпендикуляр и наклонная.

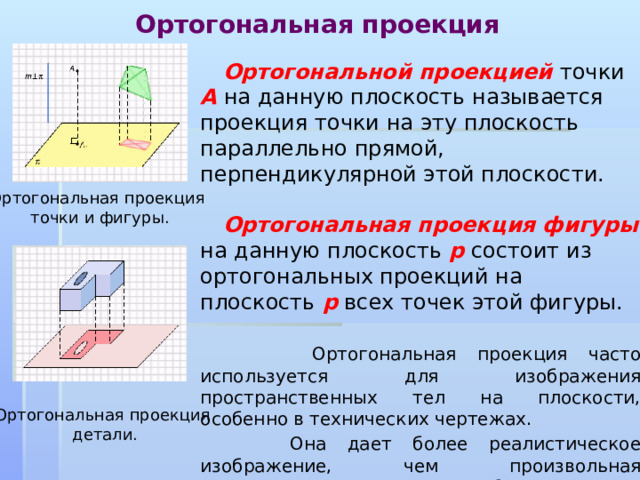
Ортогональная проекция

Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости.

Ортогональная проекция фигуры на данную плоскость p состоит из ортогональных проекций на плоскость p всех точек этой фигуры.

Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах.

Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел.

Ортогональная проекция

точки и фигуры.

Ортогональная проекция

детали.

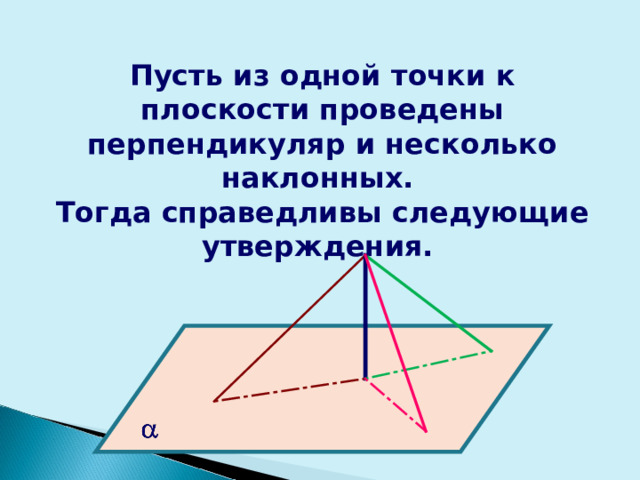
Пусть из одной точки к плоскости проведены перпендикуляр и несколько наклонных.

Тогда справедливы следующие утверждения.

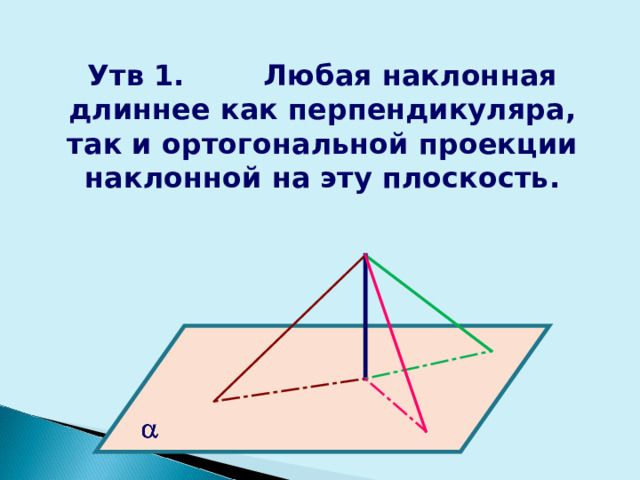
Утв 1. Любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость.

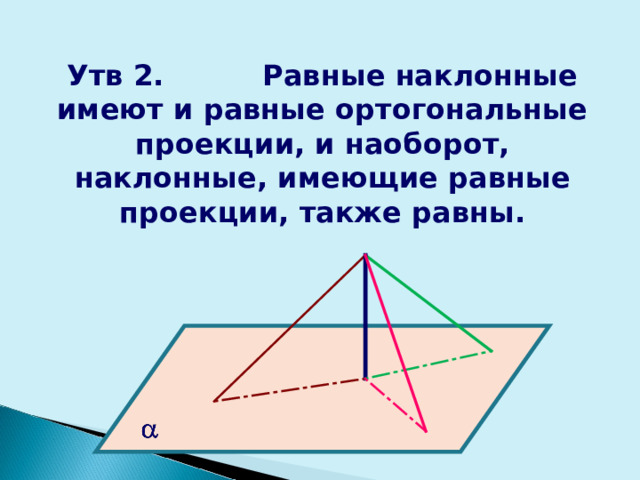
Утв 2. Равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны.

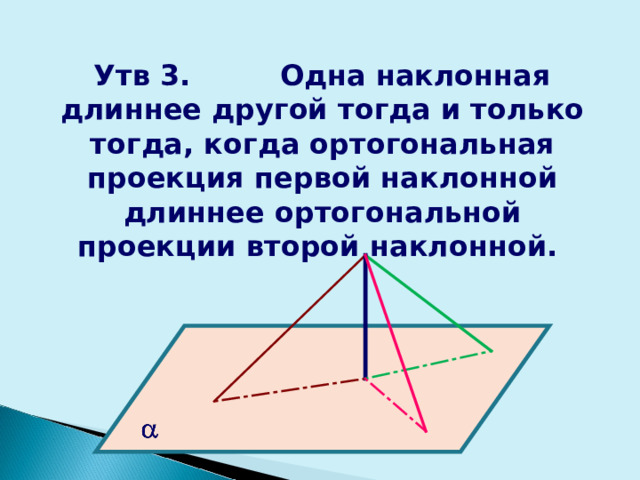
Утв 3. Одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной.

Расстояние от точки до плоскости

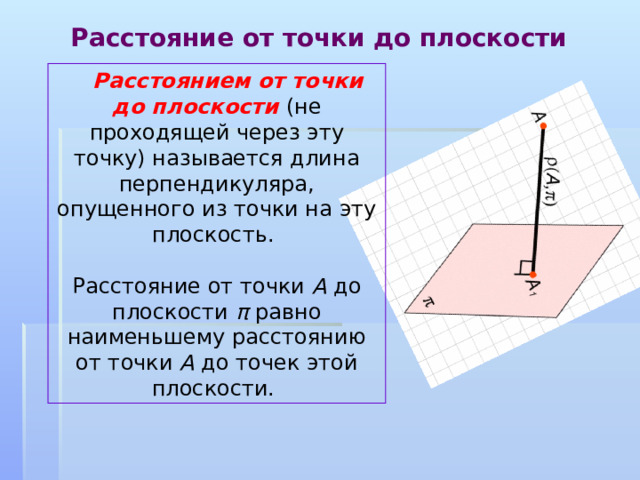
Расстоянием от точки до плоскости (не проходящей через эту точку) называется длина перпендикуляра, опущенного из точки на эту плоскость.

Расстояние от точки А до плоскости π равно наименьшему расстоянию от точки А до точек этой плоскости.

Свойство расстояния от середины отрезка

до плоскости

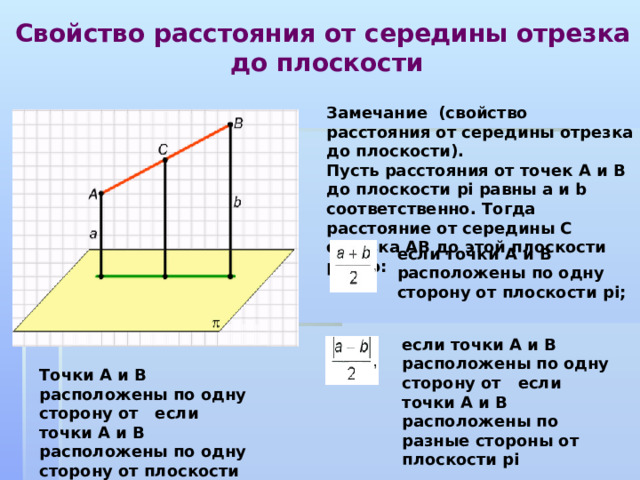
Замечание (свойство расстояния от середины отрезка до плоскости).

Пусть расстояния от точек А и B до плоскости pi равны а и b соответственно. Тогда расстояние от середины С отрезка АВ до этой плоскости равно:

если точки A и B расположены по одну сторону от плоскости pi ;

если точки A и B расположены по одну сторону от если точки А и B расположены по разные стороны от

плоскости pi

T очки A и B расположены по одну сторону от если точки А и B расположены по одну сторону от плоскости pi

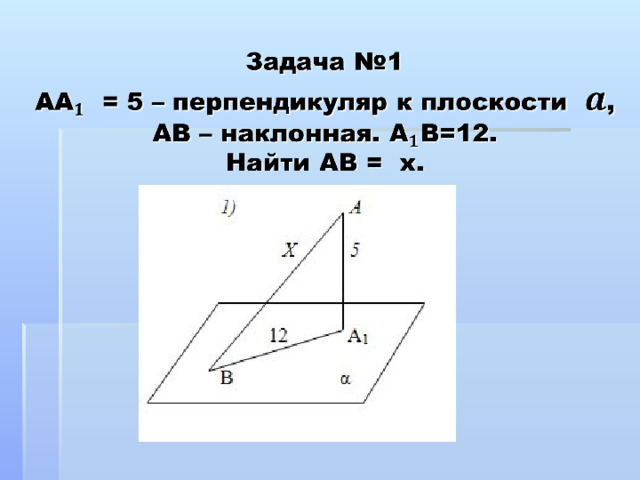
Теорема о трёх перпендикулярах.

Прямая, лежащая в

плоскости,

перпендикулярна

наклонной тогда и

только тогда, когда

она перпендикулярна

ее ортогональной

проекции.

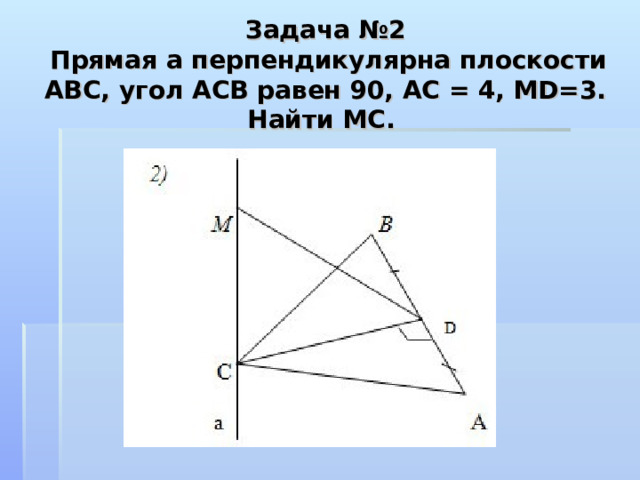
Задача №2 Прямая а перпендикулярна плоскости АВС, угол АСВ равен 90, АС = 4, МD=3. Найти МС.

Акцентируем теорию по теме.

1. Угол между прямыми равен 90˚. Как называются такие прямые?

Ответ: перпендикулярные.

2. Верно ли утверждение: «прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей этой плоскости»

Ответ: да.

3. Сформулируйте признак перпендикулярности прямой и плоскости.

Ответ: если пряма перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

4. Как определяется расстояние от точки до прямой на плоскости?

Ответ: как длина перпендикуляра, проведённого из точки к данной прямой.

5. По рисунку назовите:

перпендикуляр, основание

перпендикуляра, наклонную к

плоскости α , основание

наклонной и её проекцию на

плоскость α .

6. Сформулируйте теорему о трёх перпендикулярах.

P

D

K

α

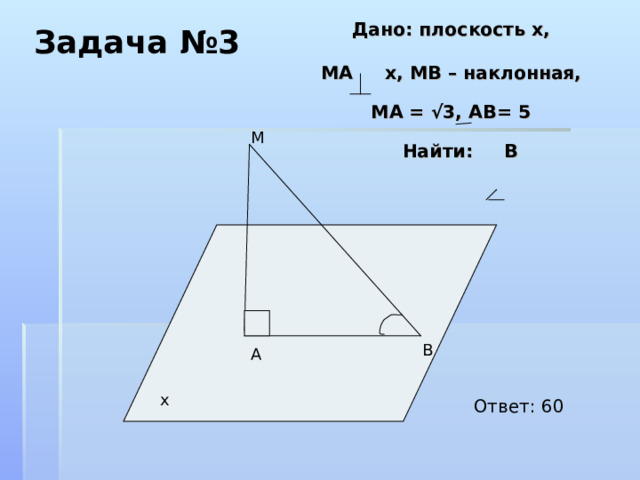
Дано: плоскость х,

МА х, МВ – наклонная,

МА = √3, АВ= 5

Найти: В

Задача №3

М

В

А

х

Ответ: 60

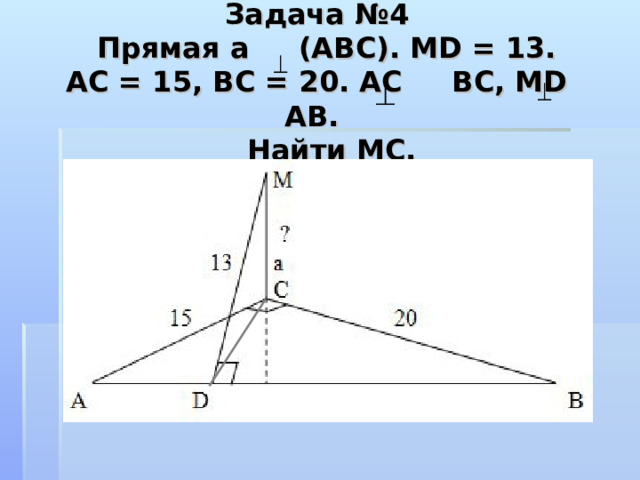
Задача №4 Прямая а (АВС). MD = 13. АС = 15, ВС = 20. АС ВС, МD АВ. Найти MC.

Думай

Задача №5

Прямая BD перпендикулярна к плоскости треугольника АВС. Известно, что BD = 9 см,

АС = 10 см, ВС = ВА = 13 см.

Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника ACD .

!

Д

У

М

А

Й

!

!

Задача 6

Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см, угол BAD равен 60 градусам, ВМ = 12,5 см.

!!!

Ш

Р

Й

А

Е

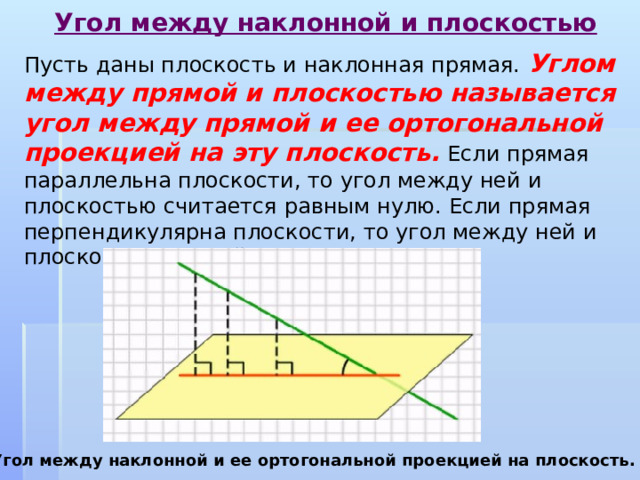
Угол между наклонной и плоскостью

Пусть даны плоскость и наклонная прямая. Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на эту плоскость. Если прямая параллельна плоскости, то угол между ней и плоскостью считается равным нулю. Если прямая перпендикулярна плоскости, то угол между ней и плоскостью прямой, т. е. равен 90°.

Угол между наклонной и ее ортогональной проекцией на плоскость.

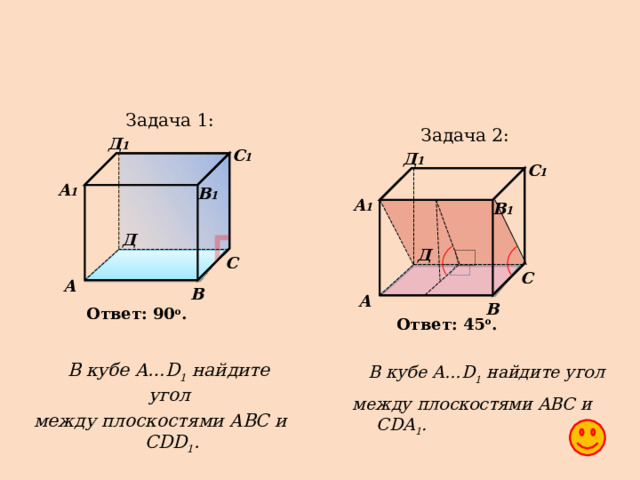
Задача 1:

Задача 2:

Д 1

С 1

Д 1

С 1

А 1

В 1

А 1

В 1

Д

Д

С

С

А

В

А

В

Ответ: 90 o .

Ответ: 45 o .

В кубе A … D 1 найдите угол

между плоскостями ABC и CDD 1 .

В кубе A … D 1 найдите угол

между плоскостями ABC и CDA 1 .

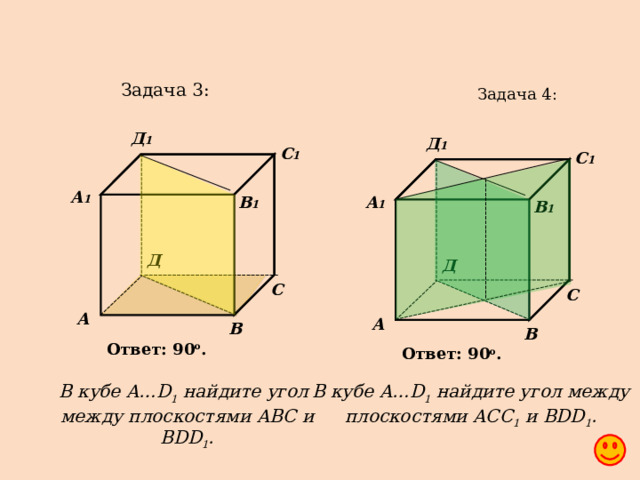
Задача 3:

Задача 4:

Д 1

Д 1

С 1

С 1

А 1

В 1

А 1

В 1

Д

Д

С

С

А

А

В

В

Ответ: 90 o .

Ответ: 90 o .

В кубе A … D 1 найдите угол между плоскостями ACC 1 и BDD 1 .

В кубе A … D 1 найдите угол между плоскостями ABC и BDD 1 .

I уровень (на «3»)

Дано:

АС ┴ ВС, SA = SB = SC =10 см; СМ =5 см –медиана.

Найти: SM (расстояние от точки S до плоскости (АВС)).

II уровень ( на «4»)

Дано:

ABCD – прямоугольник;

АК ┴ (АВС), KD = 6 см, КВ = 7 см, КС = 9 см.

Найти: расстояние от точки К до (АВС).

III уровень ( на «5»)

Дано:

АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС),

Найти: МЕ.

Разминка «Давайте вспомним»

«Учение без размышления бесполезно, но и размышление без учения опасно».

Конфуций.

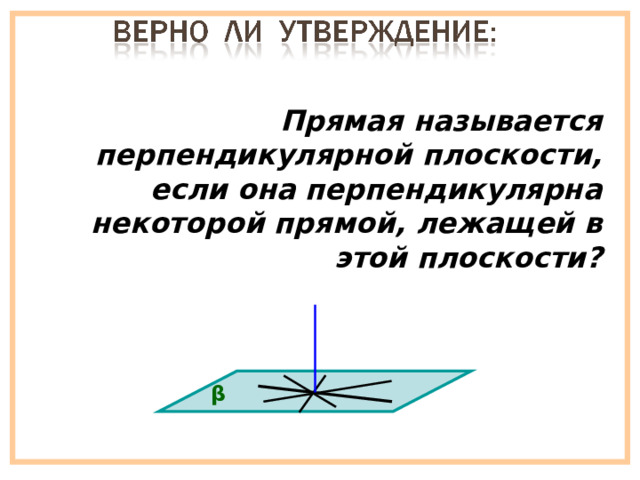
Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости?

β

А

Н

α

А

В

α

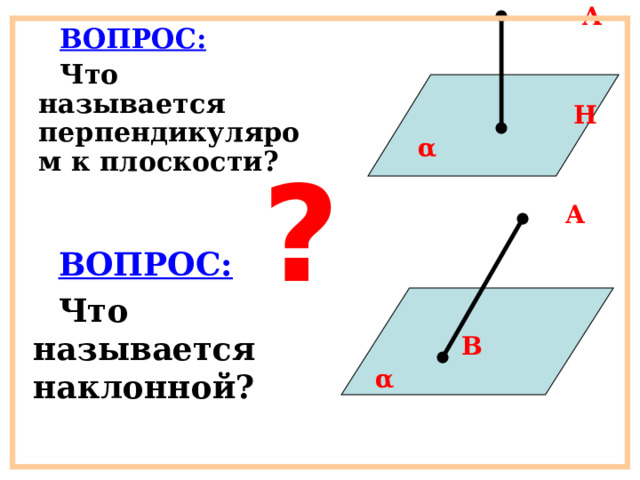
ВОПРОС:

Что называется перпендикуляром к плоскости?

?

ВОПРОС:

Что называется наклонной?

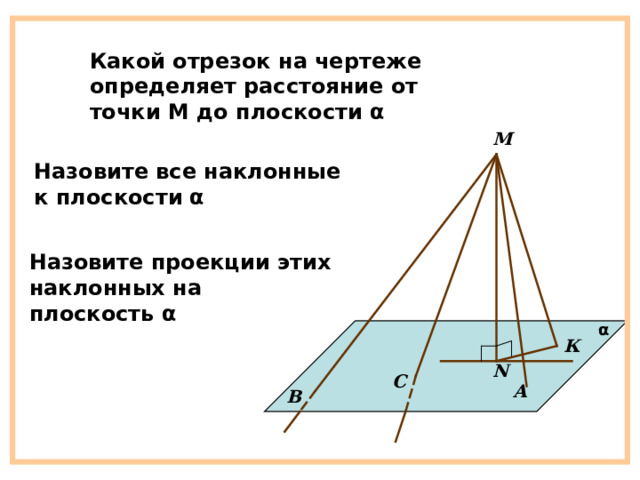
Какой отрезок на чертеже определяет расстояние от точки М до плоскости α

М

Назовите все наклонные к плоскости α

Назовите проекции этих наклонных на плоскость α

α

К

N

С

А

В

Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной на эту плоскость, то она перпендикулярна и самой наклонной.

A

а

B

C

β

Верно,

по теореме о трёх перпендикулярах

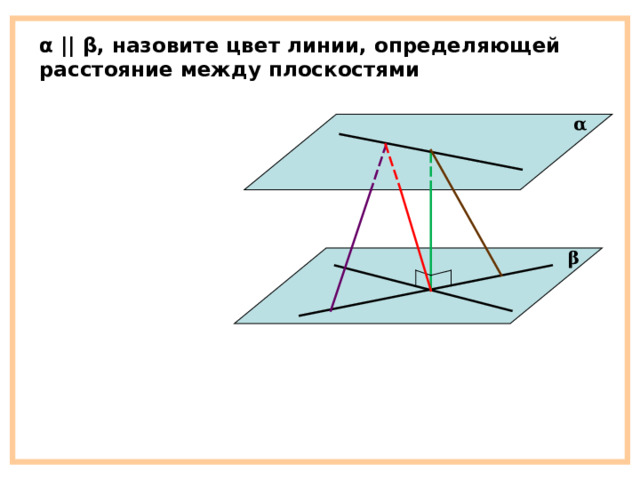
α || β , назовите цвет линии, определяющей расстояние между плоскостями

α

β

… Да, путь познания не гладок. Но знаем мы со школьных лет, Загадок больше, чем разгадок, И поиска предела нет. Пифагор.

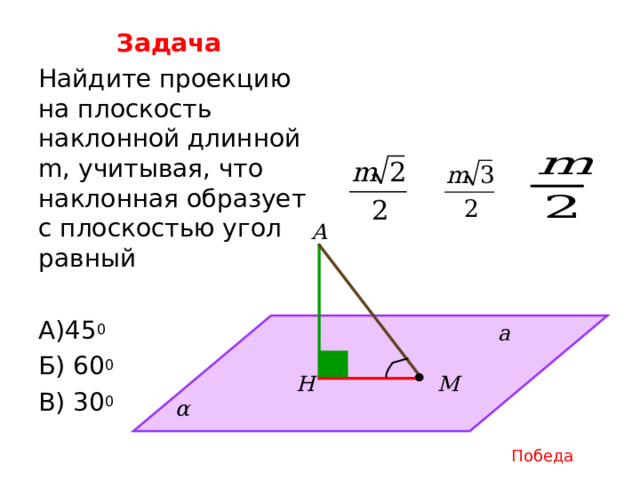
Задача

Найдите проекцию на плоскость наклонной длинной m , учитывая, что наклонная образует с плоскостью угол равный

А)45 0

Б) 60 0

В) 30 0

А

а

М

Н

α

Победа

Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие ее в точках Р и Е. Найдите РЕ,

если НР=4 см, НК=5 см, МЕ=12см.

Ответ: 12 см.

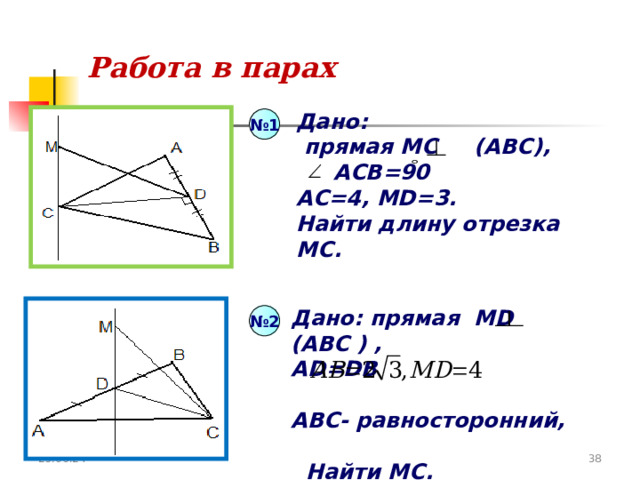
№ 1

№ 2

Работа в парах

Дано :

прямая МС (АВС),

АСВ=90

AC=4, MD=3.

Найти длину отрезка MC.

Дано: прямая MD (A ВС ) ,

AD=DB

АВС- равносторонний,

Найти МС.

25.06.24

34

Самостоятельная работа.

1 вариант.

1. Треугольник

ABC –равносторонний, точка O – его центр. Прямая OM

перпендикулярна к плоскости ABC .

a ) Докажите, что MA = MB = MC .

б) Найдите MA , если AB =6 см, MO =2см.

2 вариант.

1. ABCD – квадрат, точка O –

его центр. Прямая OM перпендикулярна к плоскости квадрата.

а) Докажите, что MA = MB = MC = MD .

б) Найдите MA , если AB =4 см, OM =1см.

2.Из точки к плоскости

проведены две наклонные. Известно , что разность длин наклонных равна 5см,а их проекции равны 7 и 18 см. Найдите расстояние от данной точки до плоскости.

2.Из точки к плоскости

проведены две наклонные. Известно , что длины наклонных равны 25 и 30см,а разность длин их проекций -1 см. Найдите расстояние от данной точки до плоскости.

25.06.24

Спасибо за урок !!!

К геометрии способность проявляй,

Не ленись, а ежедневно развивай,

Повторяй, учи, трудись, соображай,

С геометрией дружить не забывай.

Через сторону AD ромба ABCD проведена плоскость α . Найдите расстояние от прямой ВС до плоскости α , если площадь ромба равна 80 ,высота – 8 см, а угол между проекцией стороны CD и прямой AD равен 45 градусов.

Параллельные, перпендикулярные,

скрещивающиеся прямые

• festival.1september.ru
• Учительский портал
• www.cleverstudents.ru