Презентация "Теорема о трёх перпендикулярах"

Теорема о трех перпендикулярах

Цели урока:

• Доказать теорему о трёх перпендикулярах
• Научиться применять теорему о трех перпендикулярах при решении задач

1. Как называется отрезок АН?

2. Как называется точка Н?

3. Как называется отрезок АМ?

4. Как называется точка М?

5. Сравните АМ и АН.

6. Что называют расстоянием от точки А до плоскости  ?

А

Н

М





а

а

а

а

А

В







А 1

В 1















а

в

D

Дано:

AD  (ABC)

 ACB = 90 0

Доказать, что:

a ) AD  CB;

б) CB  (ADC);

В

А

в) CB  CD .

С

Теорема о трёх перпендикулярах.

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

А

Дано:



АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  НМ

Доказать, что

а  АМ.

М

Н



а

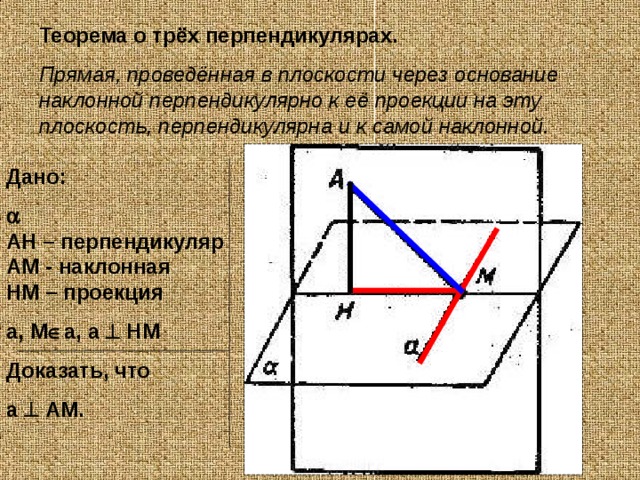
Теорема о трёх перпендикулярах.

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

Дано:



АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  НМ

Доказать, что

а  АМ.

Н

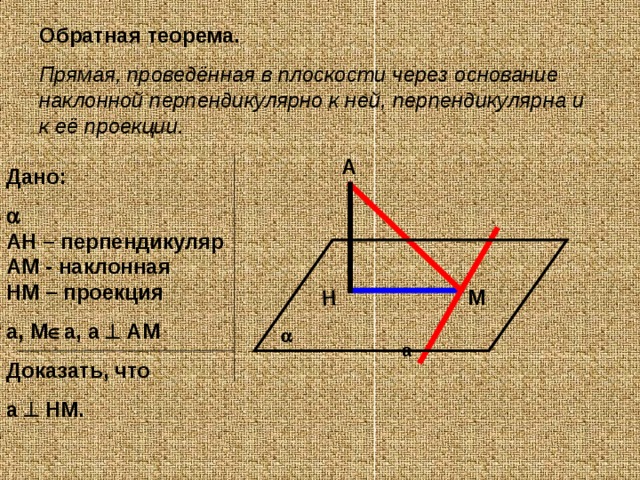
Обратная теорема.

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

А

Дано:



АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  АМ

Доказать, что

а  НМ.

М



а

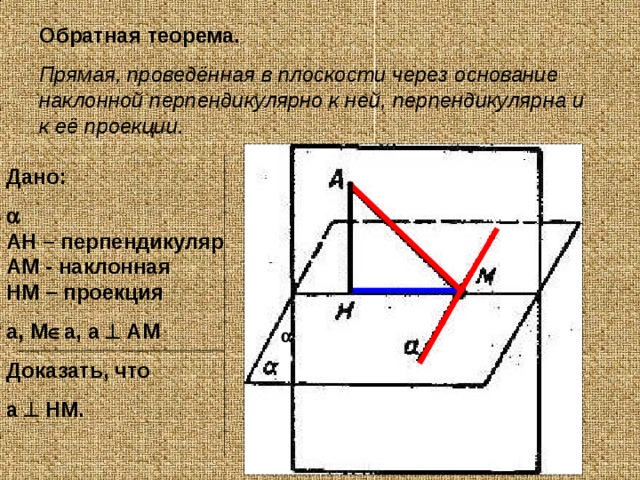
Обратная теорема.

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

Дано:



АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  АМ

Доказать, что

а  НМ.



Н

Три перпендикуляра – АН, НМ и АМ.

Дано:



АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  НМ

Доказать, что а  АМ.

Дано:

 ,

АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  АМ

Доказать, что а  НМ.

А

А

М

Н

М





а

а

Решение задач

№ 145

D

Дано:

• АВС,  С=90 0

А D  (АВС)

ВС=а DC = в

Доказать, что:

• СВ D – прямоугольный

В D - ?

С

А

В

В

М

№ 147

Дано:

АВС D – прямоугольник

МВ  (АВС D )

Доказать, что

 АМ D и  МС D - прямоугольные

А

В

D

C

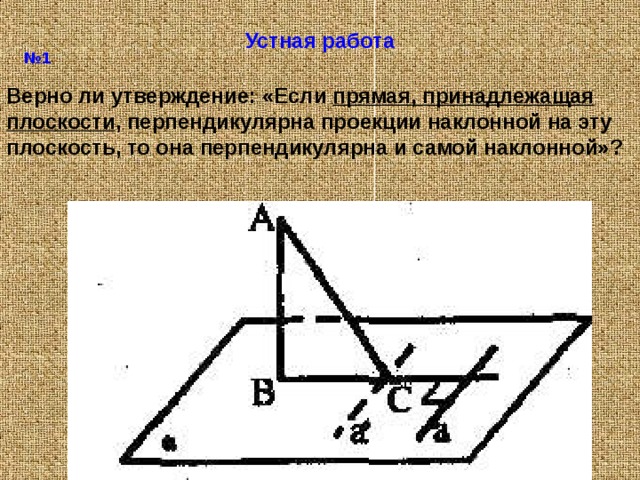
Устная работа

№ 1

Верно ли утверждение: «Если прямая, принадлежащая плоскости , перпендикулярна проекции наклонной на эту плоскость, то она перпендикулярна и самой наклонной»?

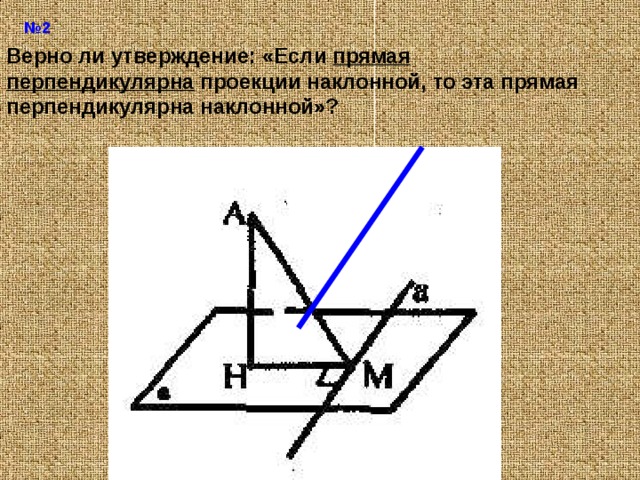
№ 2

Верно ли утверждение: «Если прямая перпендикулярна проекции наклонной, то эта прямая перпендикулярна наклонной»?

b 1

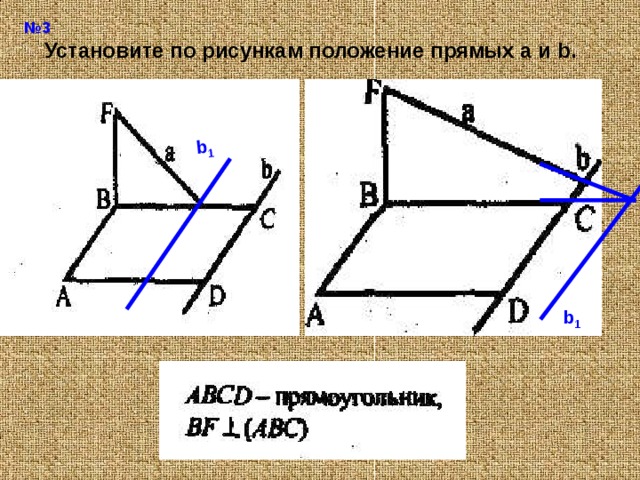
№ 3

Установите по рисункам положение прямых а и b.

b 1

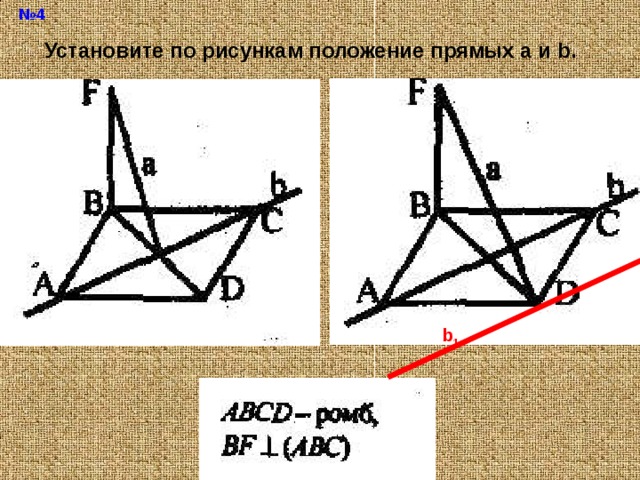
№ 4

Установите по рисункам положение прямых а и b.

b 1

Решение задач

№ 1

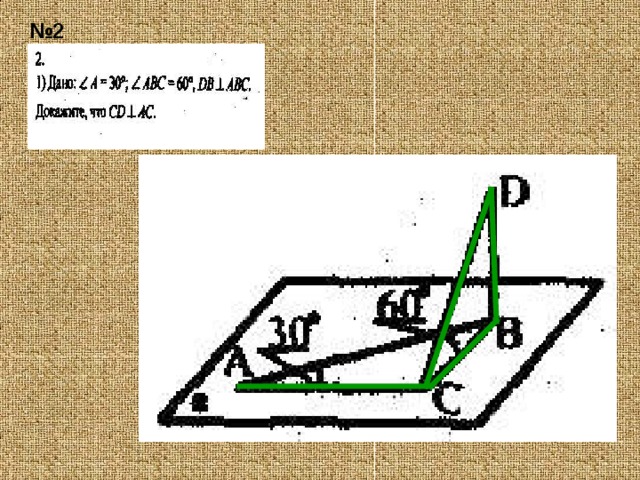
№ 2

№ 2

№ 3

№ 4

Н

Три перпендикуляра – АН, НМ и АМ.

Дано:



АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  НМ

Доказать, что а  АМ.

Дано:

 ,

АН – перпендикуляр

АМ - наклонная

НМ – проекция

а, М  а, а  АМ

Доказать, что а  НМ.

А

А

М

Н

М





а

а

Решение задач

№ 154

№ 156

Домашнее задание

п. 20 выучить теоремы

№ 148

№ 149

№ 155