Презентация по теме "Вписанная окружность"

Вписанная окружность

Определение

Если все стороны многоугольника

касаются окружности, то

окружность называется вписанной

в многоугольник,

а многоугольник – описанным около

этой окружности.

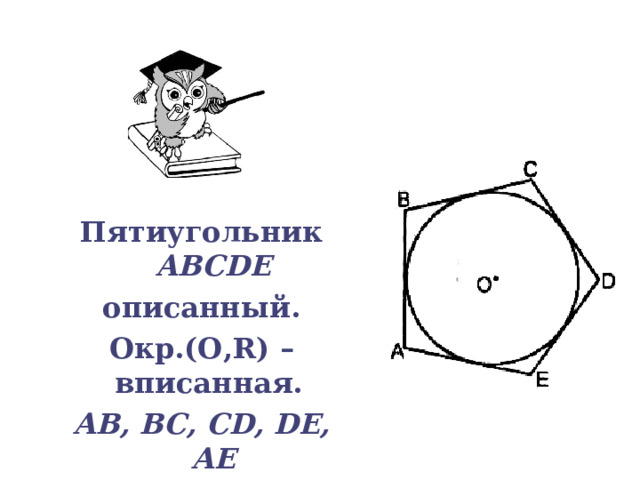
Пятиугольник ABCDE

описанный.

Окр.(О ,R) – вписанная.

АВ, ВС, CD, DE, АЕ

касательные

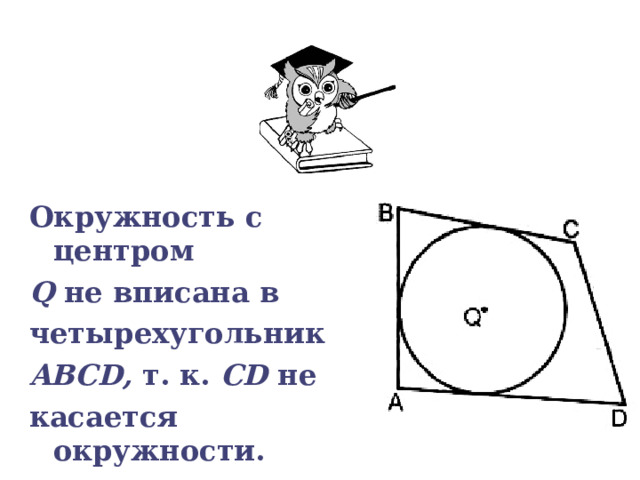
Окружность с центром

Q не вписана в

четырехугольник

ABCD, т. к. CD не

касается окружности.

ТЕОРЕМА

В любой треугольник можно

вписать окружность.

Замечание: в треугольник можно

вписать только одну окружность.

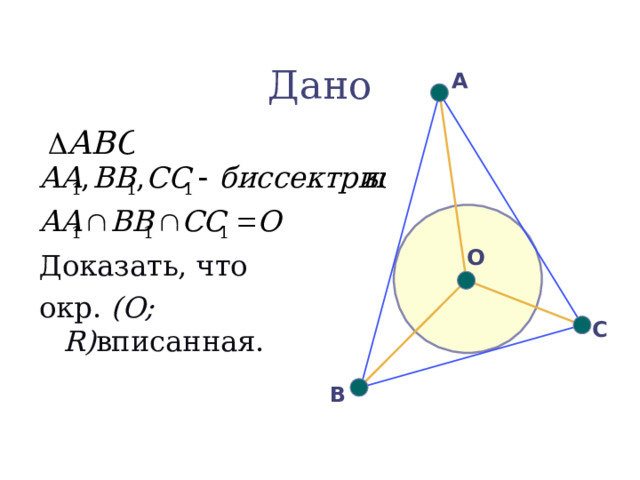
Дано

А

Доказать, что

окр. (О ; R) вписанная.

О

С

В

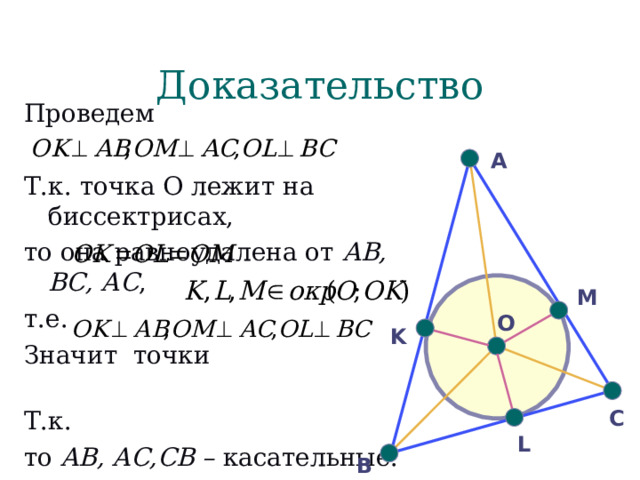
Доказательство

Проведем

Т.к. точка О лежит на биссектрисах,

то она равноудалена от АВ, ВС, АС ,

т.е.

Значит точки

Т.к.

то AB, AC,CB – касательные.

Значит окр .(О ; О R) вписанная.

А

M

О

K

С

L

В

Важный вывод 1

Центр вписанной в

треугольник окружности

лежит в точке пересечения

его биссектрис и

равноудален от его сторон.

Важный вывод 2

Радиус окружности

вписанной в треугольник

равен расстоянию от центра

окружности до сторон

треугольника.

Не во всякий четырехугольник

можно вписать окружность.

Если же в четырехугольник

можно вписать окружность, то

его стороны обладают

следующим свойством:

Свойство

В любом описанном четырехугольнике

суммы противоположных

сторон равны.

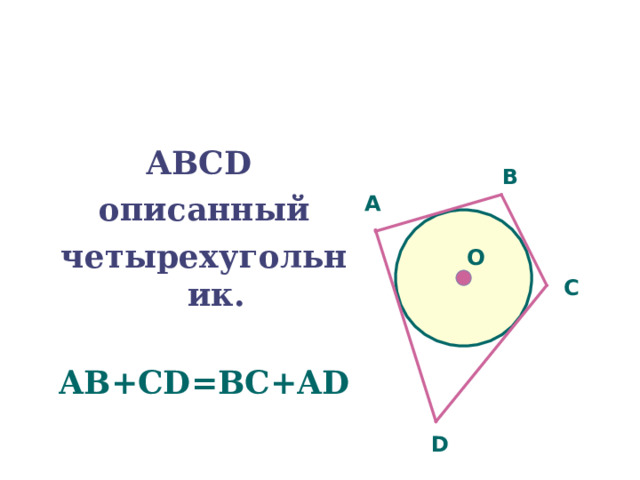
АВС D

описанный

четырехугольник.

AB+CD=BC+AD

В

А

O

С

D

Верно и обратное утверждение

Если суммы противоположных сторон

выпуклого четырехугольника равны,

то в него можно вписать окружность.

Это признак описанного

четырехугольника.

Свойство описанного многоугольника

Площадь описанного

многоугольника равна половине

произведения его периметра на

радиус вписанной окружности.