Просмотр содержимого документа
«Презентация урока по теме : "Сфера и шар"»

Тема урока: «Сфера и шар»
Выполнила:
Иманова Людмила Алексеевна
учитель математики МОБУ «Лицей 9»
г.Оренбург

Цели урока:
Обучающая: ввести понятие сферы и шара и их элементов.
Развивающая: развитие пространственного мышления, графических навыков учащихся.
Воспитательная:воспитывать критическое отношение к себе.

Математический диктант
- 1.Напишите формулу площади боковой поверхности цилиндра
- 2. Напишите 2 формулы площади боковой поверхности конуса.
- 3.Напишите формулу площади боковой поверхности усеченного конуса.
- 4.Напишите формулу площади полной поверхности конуса
- 5.Осевое сечение конуса-правильный треугольник со стороной 10см. Найдите площадь полной повехности конуса.
6.Высота и радиус основания конуса равны 2см. Через две образующие, угол между которыми равен 30°, проведена секущая плоскость. Найдите площадь сечения.

Где шар? Где сфера?

Сфера – это поверхность, состоящая из всех точек
расположенных на данном расстоянии (R)
Шар – это тело, ограниченное сферой.
от данной точки (C) .
Центр сферы (С)
Центр шара (С)
R
R
С
С
R
R
R
R
Радиус сферы (R)
Диаметр шара
Радиус шара (R)
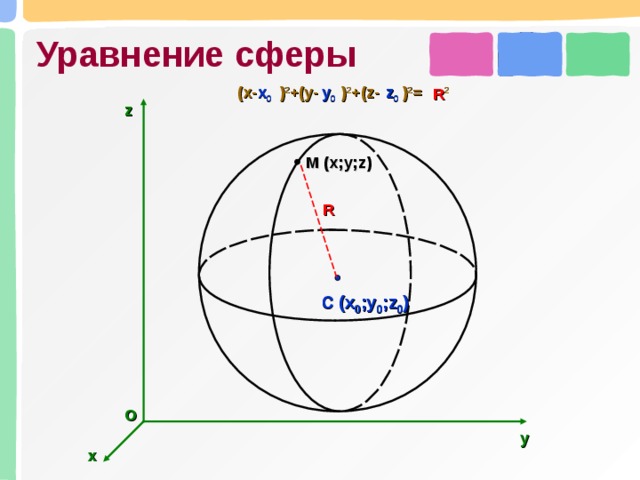
Уравнение сферы
z 0
y 0
x 0
(x- ) 2 +(y- ) 2 +(z- ) 2 = 2
R
z
M (x;y;z)
R
C (x 0 ;y 0 ;z 0 )
O
y
x
 R " width="640"
R " width="640"
Взаимное расположение сферы и плоскости
d – расстояние от центра сферы до плоскости
R – радиус сферы
z
z
z
C (0;0; d )
R
C (0;0; d )
C (0;0; d )
R
O
O
O
y
y
y
R
x
x
x
d R
d = R
d R
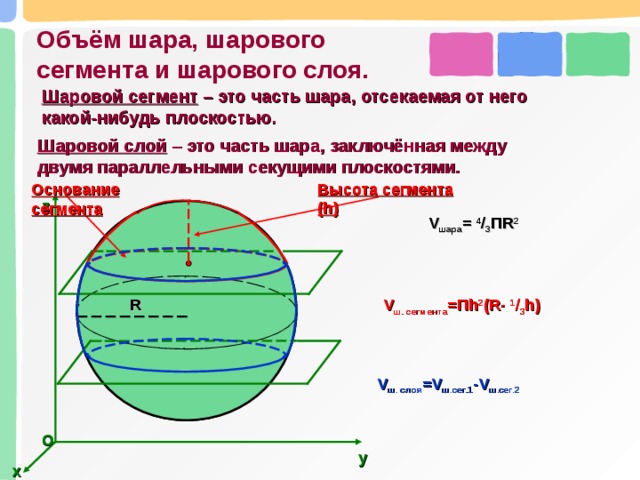
Объём шара, шарового сегмента и шарового слоя.
Шаровой сегмент – это часть шара, отсекаемая от него какой-нибудь плоскостью.
Шаровой слой – это часть шара, заключённая между двумя параллельными секущими плоскостями.
Высота сегмента (h)
Основание сегмента
z
V шара = 4 / 3 ПR 2
V ш. сегмента =Пh 2 (R- 1 / 3 h)
R
V ш. слоя =V ш.сег.1 -V ш.сег.2
O
y
x
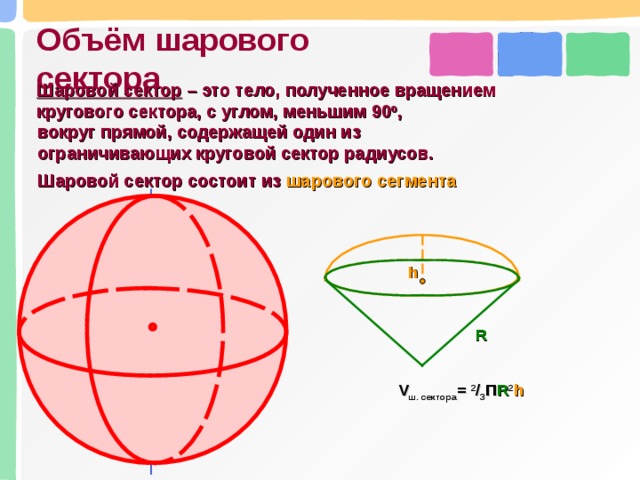
Объём шарового сектора
Шаровой сектор – это тело, полученное вращением кругового сектора, с углом, меньшим 90 о ,
вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Шаровой сектор состоит из шарового сегмента
h
R
V ш. сектора = 2 / 3 П R 2 h

Площадь сферы
R
S сферы = 4П R 2

Составить уравнение сферы радиуса R и центром О, если:
О(2; 5; 3), R=2
(х-2) 2 +(у-5) 2 +(z-3) 2 =4
О(-2;-6; 7), R=1
(х+2) 2 +(у+6) 2 +(z-7) 2 =1
О(0; 0; 1), R=
х 2 +у 2 +(z-1) 2 =5

Укажите координаты центра и радиус сферы
(х-4) 2 +(у-8) 2 +(z-1) 2 =4
х 2 +у 2 +(z+9) 2 =1
(х+52) 2 +(у+8) 2 +z 2 =3
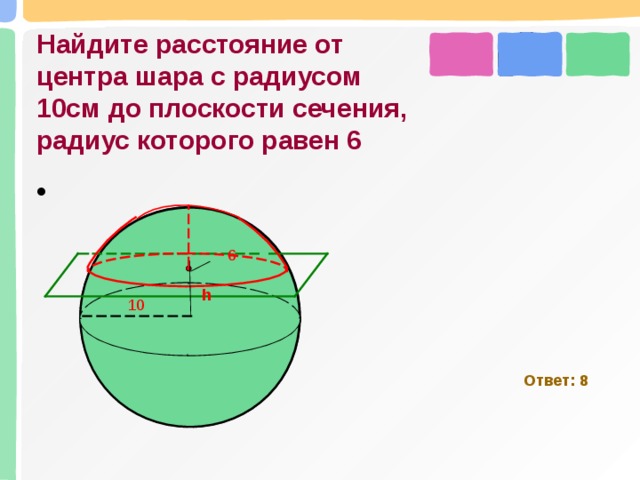
Найдите расстояние от центра шара с радиусом 10см до плоскости сечения, радиус которого равен 6
6
h
10
Ответ: 8

Задача
Диаметр шара разделён на три части в отношении 1:3:2,
через точки деления проведены перпендикулярные ему плоскости.
Найдите площадь сферы. если сумма площадей сечений равна 52 П.
Ответ: 144П

Домашнее задание
- Составить тест по теме «Сфера и шар»
- включить 4-5 теоретических вопросов и
- 4-5 задачь; расположить по мере возрастания трудности.

Спасибо за урок!













 R " width="640"
R " width="640"



















