Россия, Владикавказ
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 10.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 10.04.2025 08:11
Скодтаева Земфира Айдаруковна
Учитель астрономии, информатики, технологии, физики, математики
1 529 073
3 
Местоположение
Специализация
Презентация "Возрастание и убывание функции"
Категория:
Математика
23.06.2022 19:47
Просмотр содержимого документа
«Презентация "Возрастание и убывание функции"»
Применение производной к исследованию функции
Возрастание и убывание функции
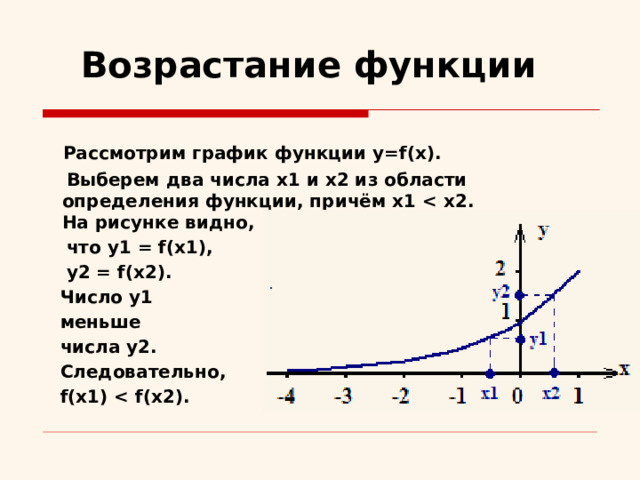
Возрастание функции
Рассмотрим график функции y=f(x).
Выберем два числа x1 и x2 из области определения функции, причём x1 На рисунке видно,
что y1 = f(x1),
y2 = f(x2).
Число y1
меньше
числа y2.
Следовательно,
f(x1)
Определение 1
Функция называется монотонно возрастающей
(или просто возрастающей) в интервале a ≤ x ≤ b,
если из условия x1
При этом a ≤ x1 ≤ b, a ≤ x2 ≤ b.
Другими словами, функция называется монотонно возрастающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему значению аргумента соответствует большее значение функции.
Примечание : представьте, что двигаясь по оси OX
слева направо, по графику функции движемся вверх.
g(x2). " width="640"
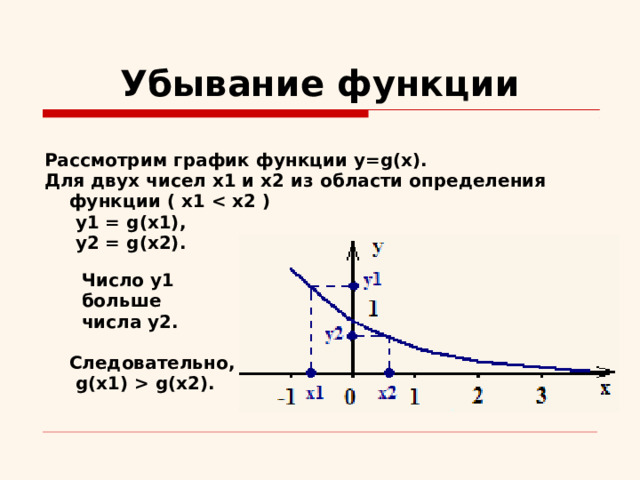
Убывание функции
Рассмотрим график функции y=g(x).
Для двух чисел x1 и x2 из области определения
функции ( x1
y1 = g(x1),
y2 = g(x2).
Число y1
больше
числа y2.
Следовательно,
g(x1) g(x2).
x1 следует, что g( x2 ) При этом а = Другими словами, функция называется монотонно убывающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему соответствует меньшее значение функции. Примечание : представьте, что двигаясь по оси OX слева направо, по графику функции движемся вниз. " width="640"
Определение 2
Функция y = g ( x ) называется монотонно убывающей
(или просто убывающей) в интервале a =
если из условия x2 x1 следует, что g( x2 )
При этом а =
Другими словами, функция называется монотонно убывающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему соответствует меньшее значение функции.
Примечание : представьте, что двигаясь по оси OX слева направо, по графику функции движемся вниз.
Промежутки монотонности
Промежутки возрастания и убывания называются промежутками монотонности функции.
Определение постоянной функции
Рассмотрим график функции y=k.
График функции - это прямая, параллельная оси OX.
Очевидно, что эта функция не возрастающая и не
убывающая на всём множестве действительных
чисел.
Определение 3.
Функция, не
возрастающая
и не убывающая
на всей области
определения
Называется
постоянной .
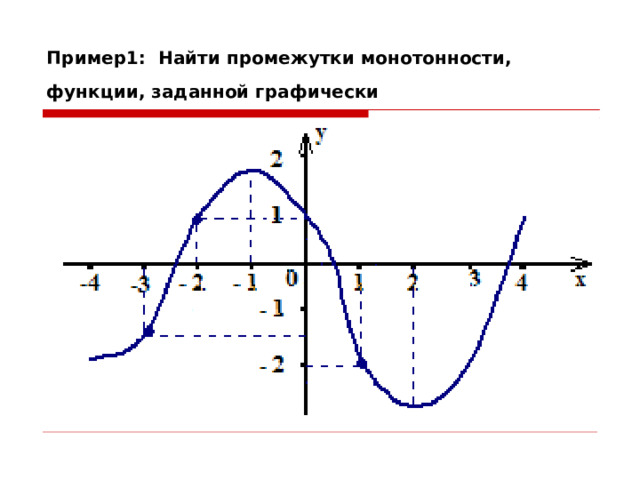
Пример1: Найти промежутки монотонности, функции, заданной графически
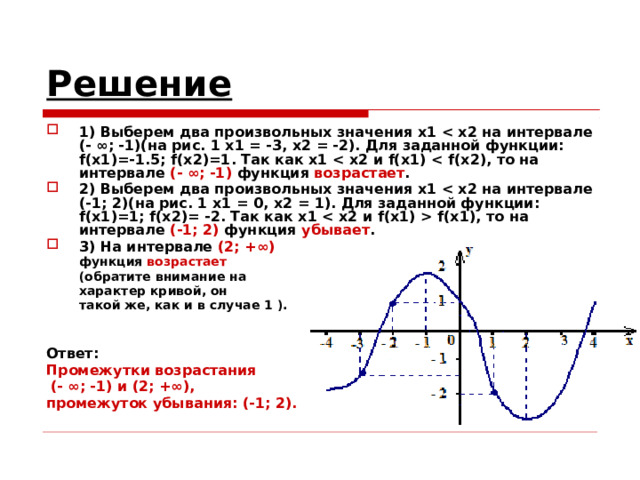
Решение
- 1) Выберем два произвольных значения x1 (- ∞; -1) функция возрастает .
- 2) Выберем два произвольных значения x1 f(x1), то на интервале (-1; 2) функция убывает .
- 3) На интервале (2; +∞)
функция возрастает
(обратите внимание на
характер кривой, он
такой же, как и в случае 1 ).
Ответ:
Промежутки возрастания
(- ∞; -1) и (2; +∞),
промежуток убывания: (-1; 2).
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 4 секунд
