Практическая работа № 1: «Приближенные вычисления»
Цель:
- научиться определять абсолютную и относительную погрешности числа;
- научиться определять верные значащие цифры числа;
- научиться определять погрешности функций.
Указания:
Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.
Порядок выполнения работы:
-
Рассмотрите теоретический материал по теме и примеры решения задач.
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы
Теоретический материал
Разность точного и приближенного значений величины называется погрешностью приближения (обозначается 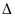 х), т.е.
х), т.е. 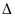 х=х-а - погрешность приближения, откуда х=а+
х=х-а - погрешность приближения, откуда х=а+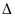 х, т.е. истинное значение равно сумме приближенного значения и погрешности приближения.
х, т.е. истинное значение равно сумме приближенного значения и погрешности приближения.
Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближенного значения числа х.
т.е. 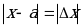 -абсолютная погрешность приближения.
-абсолютная погрешность приближения.
Запись х= а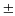 h означает, что истинное значение величины х заключено между границами, т.е. а - h
h означает, что истинное значение величины х заключено между границами, т.е. а - h 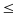 х
х 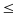 а + h
а + h
Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 -1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 - 1280 = 4.
Пример 2. Даны приближенные значения числа х =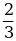 ;
; 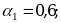
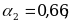
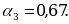 Какое из этих трех приближений является лучшим?
Какое из этих трех приближений является лучшим?
Решение: Находим 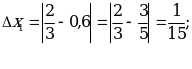
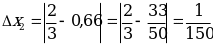 ;
; 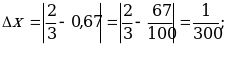 Лучшим приближением числа х является
Лучшим приближением числа х является 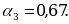
Пример 3. Длина детали х (см) заключена в границах 33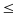 х
х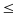 34. Найти границу абсолютной погрешности измерения детали.
34. Найти границу абсолютной погрешности измерения детали.
Решение: Примем за приближенное значение длины детали среднее арифметическое границ: а=(33+34)/2 = 33,5 (см). Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см). Величину 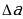 можно найти и как полуразность верхней и нижней границ, т.е.
можно найти и как полуразность верхней и нижней границ, т.е. 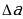 = (34-33)/2 = 0,5 (см). Длина детали х, найденная с точностью до
= (34-33)/2 = 0,5 (см). Длина детали х, найденная с точностью до 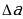 =0,5 (см), заключена между приближенными значениями числа х: 33,5-0,5
=0,5 (см), заключена между приближенными значениями числа х: 33,5-0,5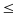 х
х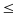 33,5+0,5; х=33,5
33,5+0,5; х=33,5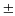 0,5 (см). Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения и обозначается
0,5 (см). Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения и обозначается 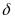 .
.
Т.е. 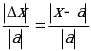 =
=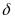 является относительной погрешностью приближения.
является относительной погрешностью приближения.
Пример 4. При измерении длины L и диаметра проводника получили L=(10,0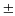 0,1) м, d = (2,5
0,1) м, d = (2,5 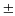 0,1) мм. Какое из этих измерений точнее?
0,1) мм. Какое из этих измерений точнее?
Решение: Измерение длины проводника производилось с точностью до 0,1м=100мм, а измерение диаметра проводника – с точностью до 0,1мм.
При измерении длины проводника допускается абсолютная погрешность в 100мм на 10000мм, и, следовательно, допустимая абсолютная погрешность составляет  измеряемой величины.
измеряемой величины.
При измерении диаметра допустимая абсолютная погрешность составляет
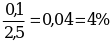 измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.
измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.
Пример 5. Известно, что 0,111 является приближенным значением для 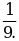 Найти абсолютную и относительную погрешности этого приближения.
Найти абсолютную и относительную погрешности этого приближения.
Решение: Здесь х=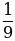 , а=0,111. Тогда
, а=0,111. Тогда 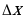 = х-а = 1/9 – 0,111 = 1/9000-а.п.п,
= х-а = 1/9 – 0,111 = 1/9000-а.п.п,
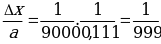 -о.п.п
-о.п.п
Пример 6. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-197 = 3. Относительная погрешность равна 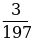 или, округленно,
или, округленно,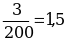 %. В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
%. В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
Пример 7. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая— 50 г. Взвешивание дало 3600 г. Это число — приближенное. Точная масса арбуза неизвестна. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит 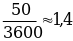 %.
%.
Самостоятельная работа
|
|
| 1 вариант | 2 вариант |
|
| 1 | Найдите абсолютную погрешность округления до единиц следующих чисел: |
|
|
| 1) 0,8; 2) 7,6; (1 балл) (1 балл) | 1) 19,3; 2) 563,58. (1 балл) (1 балл) |
|
| 2 | Граница абсолютной погрешности приближенного значения 386 числа х = 0,5. Укажите границы, в которых заключено число х. (2 балла) | Найдите границу абсолютной погрешности измерений, полученных в виде неравенства 37 . (2 балла) |
|
| 3 | Амперметр дает точность 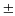 0,02 А. При измерении силы тока получили 10,63 А. Укажите границы этого числа. (2 балла) 0,02 А. При измерении силы тока получили 10,63 А. Укажите границы этого числа. (2 балла) | Атомная масса водорода 1,0082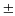 0,0005, а меди 63,44 0,0005, а меди 63,44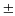 0,15. Укажите границы приближенных значений этих чисел. (2 балла) 0,15. Укажите границы приближенных значений этих чисел. (2 балла) |
|
| 4 | Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 320 рублей в воскресенье? (2 балла) | В университетскую библиотеку привезли новые учебники по геометрии для 2—3 курсов, по 280 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 7 полок, на каждой полке помещается 30 учебников. Сколько шкафов можно полностью заполнить новыми учебниками? (2 балла) |
|
| 5 | Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения? (2 балла) | Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения? (2 балла) |
|
| 6 | Граница абсолютной погрешности приближенного значения a равна h. Найдите границы, в которых заключено число x, если: |
|
|
| a=23; h=0.5; (2 балла) | a=1.5; h=0.01; (2 балла) |
|
|
|
|
|
| Критерии оценки |
|
| количество набранных баллов | оценка |
|
| 6-8 | 3 |
|
| 9-10 | 4 |
|
| 11-14 | 5 |
|
Форма контроля: Проверка письменных работ.





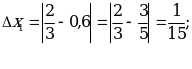
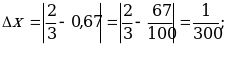 Лучшим приближением числа х является
Лучшим приближением числа х является 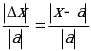 =
=


















