Презентация к уроку алгебры "Построение квадратичной функции" (9 класс).

«Ровно встали, тихо сели, Головами повертели. Очень сладко потянулись И друг другу улыбнулись. Прозвенел сейчас звонок, Начинаем наш урок»

Девиз урока: « Ум прилагается не только в знании, но и в умении прилагать знания в деле» (Аристотель)

Актуализация знаний.

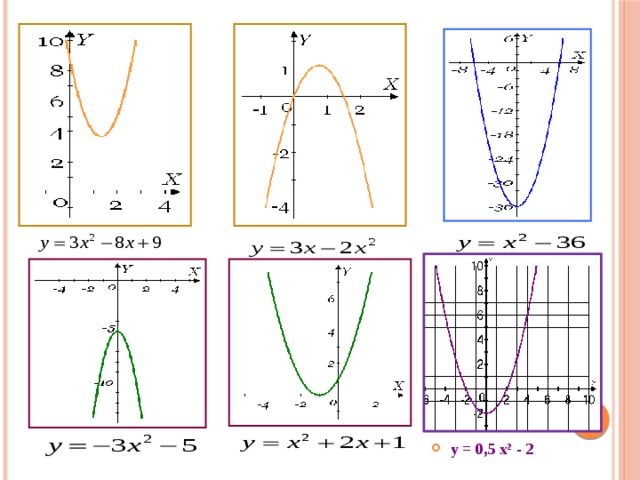
• Выбрать из приведенного списка уравнений функций только те, которые относятся к квадратичным.

Актуализация знаний.

• Выбрать из приведенного списка уравнений функций только те, которые относятся к квадратичным.

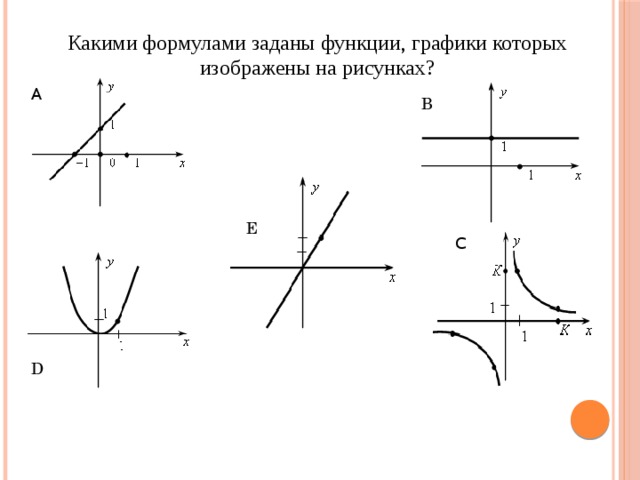
Какими формулами заданы функции, графики которых изображены на рисунках?

А

B

Е

С

D

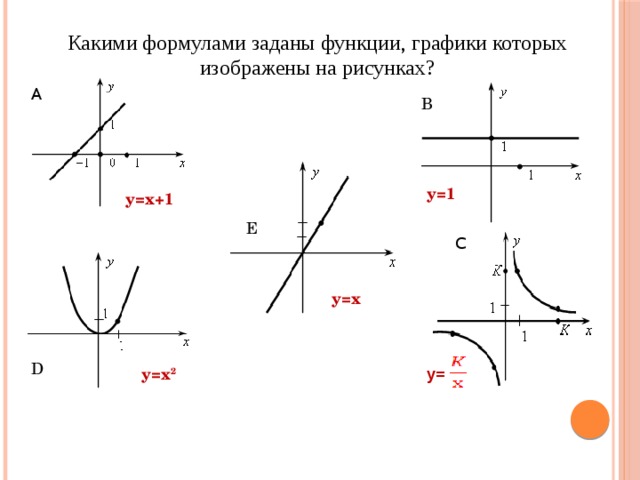
Какими формулами заданы функции, графики которых изображены на рисунках?

А

B

y=1

y=x+1

Е

С

y=x

D

y=

y=x 2

Е

Тема урока: «Построение графика квадратичной функции»

Цель урока: изучить свойства квадратичной функции, закрепить их знание при построении графиков квадратичной функции, познакомиться с алгоритмом построения любой квадратичной функции, изучить особенности расположения графика в прямоугольной системе координат; применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения поставленных задач.

• y = 0,5 x 2 - 2

0, ветви параболы направлены вверх Алгоритм построения графика квадратичной функции 1 . Построить систему координат, отметить единичный отрезок и подписать координатные оси. 2. Определить направление ветвей параболы ( a0, ветви направлены вверх, a ). 3. Определить координату х вершины параболы. Для этого нужно использовать формулу 4. Определить координату y вершины параболы. Для этого подставить в уравнение параболы найденное значение x. 5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу. 6. Построить таблицу значений. 7. Отметить полученные точки на координатной плоскости. 9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси. 10. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика. Вершина параболы Ось симметрии " width="640"

а0, ветви параболы направлены вверх

Алгоритм построения графика квадратичной функции

1 . Построить систему координат, отметить единичный отрезок и подписать координатные оси.

2. Определить направление ветвей параболы ( a0, ветви направлены вверх, a ). 3. Определить координату х вершины параболы. Для этого нужно использовать формулу

4. Определить координату y вершины параболы. Для этого подставить в уравнение параболы найденное значение x.

5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу.

6. Построить таблицу значений.

7. Отметить полученные точки на координатной плоскости.

9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси.

10. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика.

Вершина параболы

Ось симметрии

0, ветви направлены вверх, a ). 3. Определить координату х вершины параболы. Для этого нужно использовать формулу 4. Определить координату y вершины параболы. Для этого подставить в уравнение параболы найденное значение x. 5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу. 6. Построить таблицу значений. 7. Отметить полученные точки на координатной плоскости. 9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси. 10. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика. x -3.0 y -2.0 12 5 -1.0 0 0 1.0 -3 2.0 -4 -3 3.0 4.0 0 5.0 5 12 " width="640"

Задание. Построить график параболы у = х 2 -2x-3

Алгоритм построения графика квадратичной функции

1 . Построить систему координат, отметить единичный отрезок и подписать координатные оси.

2. Определить направление ветвей параболы ( a0, ветви направлены вверх, a ). 3. Определить координату х вершины параболы. Для этого нужно использовать формулу

4. Определить координату y вершины параболы. Для этого подставить в уравнение параболы найденное значение x.

5. Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Оу.

6. Построить таблицу значений.

7. Отметить полученные точки на координатной плоскости.

9. Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси.

10. Подписать график либо на выноске, либо, если позволяет место, вдоль самого графика.

x

-3.0

y

-2.0

12

5

-1.0

0

0

1.0

-3

2.0

-4

-3

3.0

4.0

0

5.0

5

12

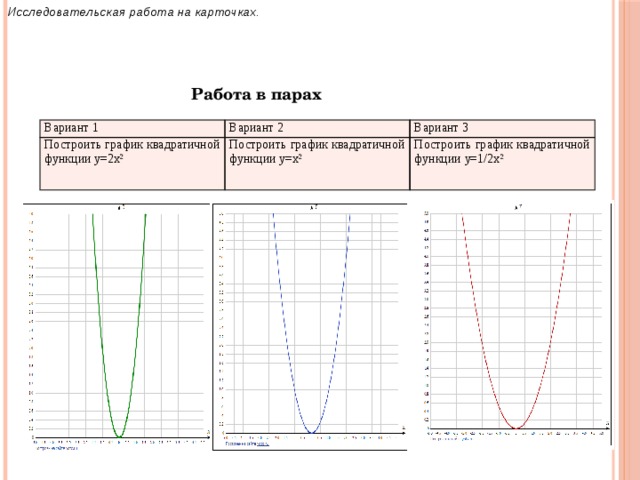
Исследовательская работа на карточках.

Работа в парах

Вариант 1

Вариант 2

Построить график квадратичной функции y=2x 2

Вариант 3

Построить график квадратичной функции y=x 2

Построить график квадратичной функции y=1/2x 2

Домашняя работа на карточках.

Красная карточка:

Ответьте на вопросы.

1. Какая функция:

а) является квадратичной,

б) назовите коэффициенты a, b, c у квадратичных функций;

в) определите направление ветвей параболы:

1) y = 2x² + x + 3;

2) y = 5x + 1;

3) y = 4x²;

4) y = 3x² - 1;

5) y = x³ + 7x - 1;

6) y = -3x² + 2x;

7) y = 6x³ - 5x² + 4x + 9;

8) y = 2х4.

№ 199(а)

Зеленая карточка:

Вместо многоточия вставить пропущенные слова.

1. Функция вида y = ax² + bx + c, где a, b и c заданные … числа, … ≠ 0,

x - … переменная, называется … функцией.

2. Функция y = x² - это … функция y = ax² + b… + c, при a = …, b = …, c = ….

3. Значения x, при которых квадратичная функция y (x) = 0, называются … этой функции.

4. Кривая, являющаяся графиком функции y = x², называется … .

5. Парабола y = x² касается оси ОХ в точке с координатами ( …; …).

6. График функции y = x² симметричен относительно оси … .

7. Ось ОУ является осью … параболы.

8. Точку пересечения параболы с её осью … называют … … .

9. Функция y = x² является … на промежутке x ≥ 0 и убывающей на промежутке x…0 .

При a … 0 ветви параболы y = ax² + bx + c направлены вверх, а при a … 0 - вниз.

№ 200(б).

• Рефлексия .

У вас три карточки: зелёная и жёлтая и красная. Если вам понравился наш урок это было интересно, полезно, вам было все понятно– покажите мне зелёную карточку, если остались какие-то вопросы или что-то не понравилось- желтую, а если совсем не понравился урок и было не понятно- красную.