Презентация к уроку "Касательная к окружности"

Общая часть

Предмет

геометрия

8 класс

Тема

Касательная к окружности

Планируемые образовательные результаты

Предметные

Метапредметные

Личностные

• Ввести понятие касательной к окружности,

• изучить свойство касательной, свойство отрезков касательных.

• коммуникативных – формирование мыслительной, речевой деятельности, навыка сотрудничества;

• регулятивных – умение управлять собственной деятельностью

• развивать умение излагать материал кратко, обобщённо (в виде схем, таблиц, алгоритмов)

• смыслообразование – умение субъектного целеполагания (постановка учебных целей самим учеником, сознательно принимает решение);

• самоопределение – самооценка (оценка результатов собственной деятельности на уроке).

Решаемые учебные проблемы

В процессе решения проблемы учащиеся научатся формулировать свойство касательной и доказывать теорему, выражающую свойство отрезков касательных, применять полученные знания к решению простейших задач.

Вид используемых на уроке ИКТ

Презентация

Методическое назначение средств ИКТ

Усилить мотивации, повысить интерес и расширить познавательные потребности обучаемых.

Усилить наглядность.

Организационная структура урока

Этап 1. Вхождение (погружение) в тему урока и создание условий для осознанного нового восприятия материала.

Формирование конкретного образовательного материала

Формулировка темы, цели и задач урока.

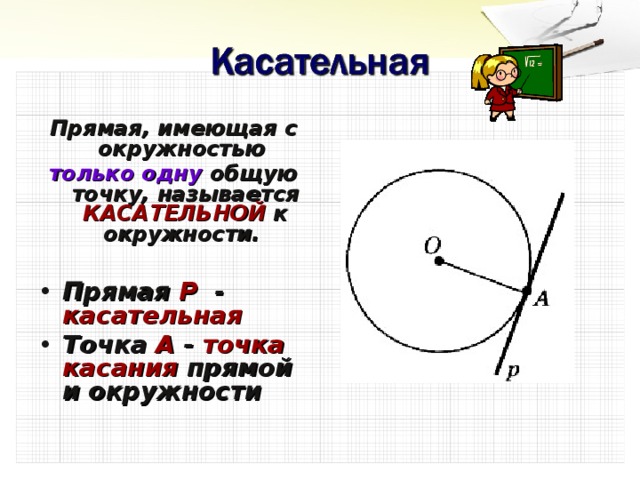
Основной вид деятельности, направленный на формирование образовательного результата.

Давайте переформулируем условие проекта на геометрический язык.

Дорожка – это… Граница бассейна – это….

- как расположена прямая по отношению к окружности? (имеет одну общую точку). А как иначе можно сказать про эту прямую, то есть как проходит по отношению к окружности? (касается)

-И поэтому эта прямая называется касательной.

- Как вы думаете какая тема нашего урока? (Касательная к окружности.(пишем на доске и в тетради, делаем чертеж- окр., касательная, точка -подписать)

- Пусть нам задана окружность – начертите в тетради любого радиуса, отметим на ней точку. Проведите касательную. А общая точка называется -точка касания.

- Касательная обладает свойствами, имеющими ценность при решении задач.

- Как вы думаете, что мы будем изучать на уроке? (касательную, ее свойства)

- А для чего нужно их изучить нам? (чтобы решать задачи)

- Итак, сегодня на уроке мы изучим свойства касательной и научимся применять их на практике.

Методы обучения

Мозговой штурм

Формы организации деятельности учащихся. Роль учителя.

Подготовка к формулированию целей и задач урока, организация деятельности.

Основные виды деятельности учителя

Организация погружения в тему, подготовка к освоению материала.

Этап 2. Организация и самоорганизация учащихся в ходе дальнейшего повторения и обобщения материала.

Организация обратной связи.

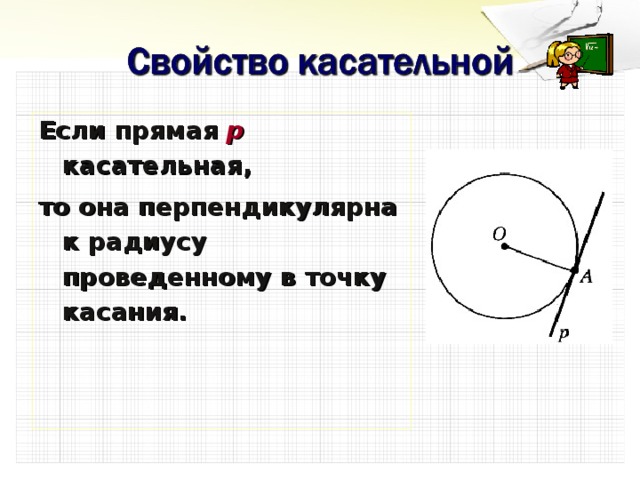
Формирование конкретного образовательного материала

Исследовательская работа

- Вернемся вновь к нашему проекту и я предлагаю вам провести небольшую творческую работу, в результате которой мы и познакомимся с одним из свойств касательной. Работу выполните согласно инструкции.

Инструкция для творческой работы.

1. Проложите дорожку к бассейну по – другому,

соблюдая все заданные условия.

1. Обозначьте точки касания буквами В и С.

2. Соедините центр бассейна с точками касания.

3. Определите градусную меру углов между

радиусами и касательными.

1. Сделайте вывод.

- Какой вывод вы получили? (спросить в двух группах)

- Это и есть одно из свойств касательной:

«Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания».

.

Основной вид деятельности, направленный на формирование образовательного результата.

1. Формирование системы научных знаний.

2. Использование знаний по предмету для решения конкретных задач.

Методы обучения

Работа в паре, фронтальный опрос.

Средства ИКТ для реализации данного вида деятельности

Презентация

Формы организации деятельности учащихся. Роль учителя.

Обсуждение. Создание личного продукта.

Организация деятельности.

Основные виды деятельности учителя

Организация. Разработка образца для сравнения личного продукта.

Этап 3. Практикум

Формирование конкретного образовательного материала

Решение практических задач

Основной вид деятельности, направленный на формирование образовательного результата.

Индивидуальная работа

Методы обучения

поисковый

Средства ИКТ для реализации данного вида деятельности

Презентация

Формы организации деятельности учащихся.

Роль учителя.

Работа с задачами на готовых чертежах. Выполнение задания.

Организация, консультация

Основные виды деятельности учителя

Организация работы в парах ,организация индивидуальной работы учащихся.

Адресная помощь

Этап 4. Подведение итогов, домашнее задание.

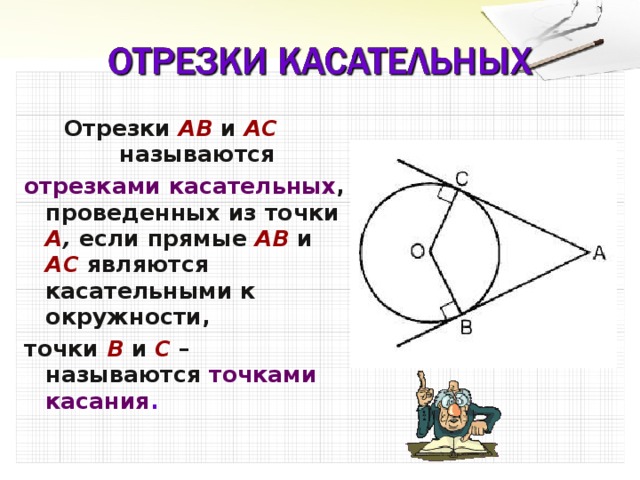
Рефлексия по достигнутым либо недостигнутым результатам

Как вы думаете в жизни можно встретить касательную к окружности?

-Все катались на велосипеде? Обращали внимание на цепь, которая помогает движению колес? Видим касательную? (даже 2)-слайд.

- А кто из вас помогал делать ремонт автомобиля?

- Обращали внимание на ремни – с помощью, которых происходит передача механической энергии от двигателя, различные конвейеры.

- Воздушный шар, наполненный горячим воздухом, на котором передвигались по воздуху.

Это говорит о том, что геометрические задачи находят широкое практическое применение: в инженерном деле, физике, строительстве и многих других областях

Вопросы:

1)Какая прямая называется касательной к окружности?

2)Назовите случаи взаимного расположения прямой и окружности?

3) Какая точка называется точкой касания?

4) Как наиболее точно провести касательную к окружности?

5) Сколько радиусов можно провести перпендикулярно к данной касательной?

6) Что вы знаете об отрезках касательных?

Этап 5. Домашнее задание.

Индивидуальные листы каждому из учащихся.

.

Используемые технологии

Мозговой штурм.

Формирование УУД

Коммуникативные

Умение слушать и слышать друг друга, точно выражать свои мысли в соответствии с задачей и условиями ситуации; вступать в диалог и участвовать в коллективном обсуждении проблемы.

Умение устанавливать и сравнивать разные точки зрения, аргументировать свою позицию.

Обмениваться знаниями с другими людьми для принятия совместного решения.

Познавательные

Умение анализировать известный материал

Умение формулировать собственные цели-мотивы

Умение делать выводы, обобщения и умозаключения.

Регулятивные

Планирование цели своей деятельности, пути её достижения.

Решение задач и принятие ответственности за это решение.

Умение контролировать своё эмоциональное состояние и поведение.

Способы оценки на уроках

Словесная оценка, отметка по диагностической карте.