Получите доступ к огромной базе учебных материалов на каждый урок с возможностью удалённого управления...

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 02.06.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 11.02.2023 08:04

Железнова Людмила Михайловна

учитель математики

54 года

16 384

2 044

Подписчики

Подписки

Местоположение

Россия, Новосибирская область, Татарский район, с.Новомихайловка

Специализация

Математика

Классному руководителю

Обо мне Блог Файлы Тесты Галерея Активность Награды

Презентация к уроку по теме "Размещения", 9 класс

Категория: Математика

25.04.2017 12:22

Просмотр содержимого документа
«Презентация к уроку по теме "Размещения", 9 класс»

Размещения

9 класс

Математика нужна, Без нее никак нельзя. Учим, учим мы, друзья, Что же помним мы с утра?

«Прямо поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься»

«Приобретать знания – это храбрость, приумножать знания – это мудрость, а умело применять – великое искусство»

Восточная мудрость

Теоретическая разминка !

Что называется комбинаторикой?
Что означает слово «комбинаторика»?
Какие вы знаете методы комбинаторики?
Что такое перестановки?
По какой формуле вычисляется число перестановок из n элементов?
В каких областях знаний нашли широкое применение методы комбинаторики?

Области применения комбинаторики:

учебные заведения ( составление расписаний);
сфера общественного питания (составление меню);
агротехника (размещение посевов на полях);
география (раскраска карт);
биология (расшифровка кода ДНК);
лингвистика (рассмотрение вариантов комбинаций букв);

Области применения комбинаторики:

спортивные соревнования (расчёт количества игр между участниками);
химия (анализ возможных связей между химическими элементами);
экономика (анализ вариантов купли-продажи акций);
доставка почты (рассмотрение вариантов пересылки);
военное дело (расположение подразделений).

Самостоятельная работа

«Прежде чем решать задачу – прочитай условие !»

Жак Адамар

1) Установите соответствие

А)

Б)

В)

Г)

Д)

Проверка !

2) Из букв a, b, c, d составлены различные комбинации. Какие из них не являются перестановками?

1) a, b, d

4) a, c, b, d

2) b, c, a

7) d, d, c, c

5) c, d, b, a

3) c, a, d

6) b, c, a, d

8) b, a, c, b

9) d, d, a, a

Проверка !

2) Из букв a, b, c, d составлены различные комбинации. Какие из них не являются перестановками?

1; 2; 3; 7; 8; 9

1) a, b, d

2) b, c, a

4) a, c, b, d

7) d, d, c, c

5) c, d, b, a

3) c, a, d

8) b, a, c, b

6) b, c, a, d

9) d, d, a, a

Задача !

3) Государственные флаги некоторых стран состоят из трёх горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?

Решение задачи

Р 3 = 3! = 1 ∙ 2 ∙ 3 = 6

Ответ: 6 вариантов.

Комбинаторика

В течение 1 минуты составьте как можно больше слов, состоящих из букв слова КОМБИНАТОРИКА

Проверка !

Ком, комбинат, комбинатор , тор, рот, банк, банка, кот, ток, рота, тина, тон, нота, каток, мина, бином, мот, том, икра, мир,…

Математический диктант

1. Какой раздел математики изучает перестановки?

а) Логика б) Алгебра

в) Геометрия г) Комбинаторика

2. Перестановкой из n элементов называется каждое расположение в _________ определённом порядке.

а) других элементов б) этих элементов

в) части элементов г) дополнительных элементов

3. Значение 4! =

а) 2 б) 36 в)24 г)20

4. Сколькими способами можно разместить на трёхместной скамье троих учеников?

а) 24 б) 8 в) 12 г) 6

5. Сколько различных четырёхзначных числа можно составить из цифр 9,8,7 и 6 без повторения их в записи числа?

а) 24 б) 120 в) 30 г) 12

Проверка !

Задача!

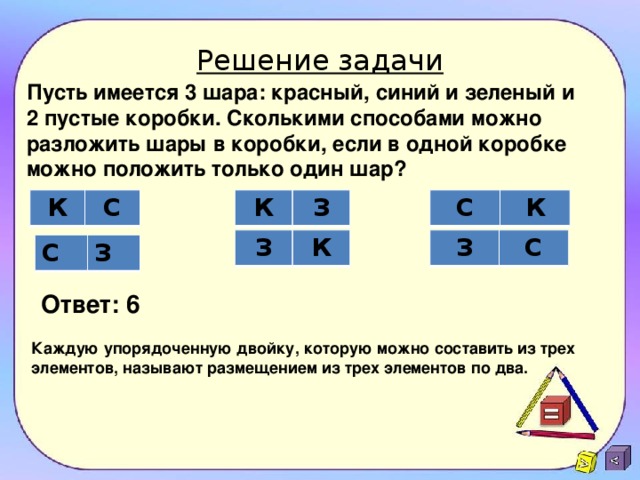
Пусть имеется 3 шара: красный, синий и зеленый и 2 пустые коробки. Сколькими способами можно разложить шары в коробки, если в одной коробке можно положить только один шар?

Решение задачи

Ответ: 6

Каждую упорядоченную двойку, которую можно составить из трех элементов, называют размещением из трех элементов по два.

Определение

Запомните !

Размещением из n элементов по k (k ≤ n) называется любое множество, состоящее из k элементов, взятых в определенном порядке из данных n элементов.

Если k =n, то формула …?

Тест по теме «Размещения»

«Математику нельзя изучать, наблюдая, как это делает сосед»

Айвен Нивен

Тест по теме « Размещения »

1) Из 5 обучающихся 9 класса надо выбрать завуча класса, старосту и физорга . Сколькими способами это можно сделать?

а) 6 б) 60 в) 120

2) Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?

а) 24 б) 36 в) 12

3) На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?

а) 680 б) 720 в) 840

4) На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места 2 фотографии?

а) 30 б) 12 в) 24

5) В конкурсе песен участвуют 15 человек. Сколькими способами могут распределиться между ними 1 ое , 2 ое , и 3 е места?

а) 24360 б) 2730 в) 6720

Проверка !

2017

2017

Домашнее задание

Повторить п. 32;

№ 758; № 767,

карточка «ОГЭ».

Составить интересную задачу практической направленности по данным школьной жизни (по желанию)

Работа в парах

ОГЭ, № 19

Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?

Проверка !

1 бросок

2 бросок

3 бросок

Ответ: 8 способов

Дополнительное задание

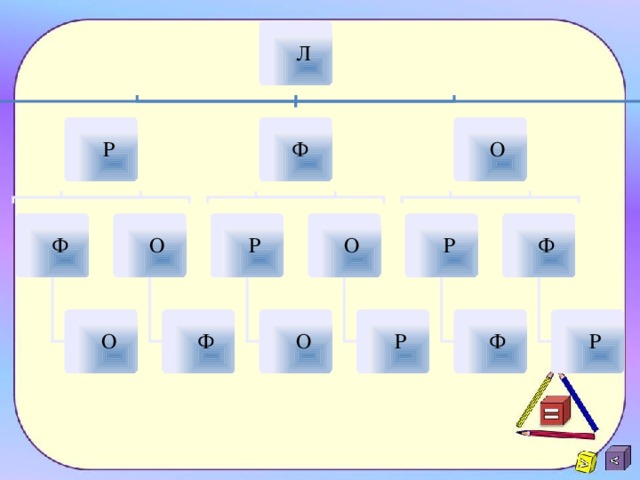
Составить расписание на завтра из 5 уроков: математика, литература, обществознание, русский язык, физкультура. Сколько можно составить вариантов расписания на день, зная точно, что математика – последний урок?

«Счастлив тот, кто имеет возможность выбора»

Блез Паскаль

Р 4 = 4!=24 24 варианта расписания!

ЛОРФ

ЛОФР

ОЛФР

ОЛРФ

ЛРОФ

РЛФО

ФЛРО

РЛОФ

ОРЛФ

ЛРФО

ОРФЛ

ФРЛО

ЛФОР

РОЛФ

ФОЛР

РОФЛ

ЛФРО

ОФЛР

ФОРЛ

ОФРЛ

РФЛО

ФЛОР

РФОЛ

ФРОЛ

Дополнительное задание

Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр

2, 0, 1, 7?

Решение:

Из цифр 2, 0, 1, 7 можно получить Р 4 перестановок. Из них надо исключить те перестановки, которые начинаются с 0. Число таких перестановок равно Р 3. Значит, искомое число четырехзначных чисел равно Р 4 – Р 3 .

Получаем Р 4 – Р 3 = 4!-3! = 24-6=18.

Оцени себя!

8 - 10 баллов- «3»;
11 -15 баллов- «4»;
Больше 16 баллов - «5».

Подведем итоги!

Что сегодня на уроке мы повторили?
Что изучили?
Для чего вы это делали?
Может ли нам комбинаторика помочь в реальной жизни?

Оцени своё отношение!

– урок полезен, все понятно.

– лишь кое-что чуть-чуть неясно, ещё придется потрудиться.

– да, трудно все-таки учиться!

Всем спасибо за урок!

До новых встреч!

Притча

Шел мудрец, а навстречу ему три человека везли под горячим солнцем тележки с камнями для строительства Храма. Мудрец остановился и задал каждому по вопросу.

У первого спросил: « Что ты делал целый день?» И тот с ухмылкою ответил, что целый день возил проклятые камни.

У второго спросил: « А ты что делал целый день?»

И тот ответил: « Я добросовестно выполнял свою работу».

А третий улыбнулся ему, лицо засветилось радостью и удовольствием, и ответил:

«А я принимал участие в строительстве Храма».

- Ребята! Кто работал, так как первый человек?

-Кто работал добросовестно?

-А кто принимал участие в строительстве Храма знаний?