Презентация на тему " Многочлены"

7 класс Арифметические операции над многочленами

Задания для интерактивной доски

МОУ Барановская сош

После многочисленного перерыва, длившегося пятнадцать столетий, были возрождены Олимпийские игры. Произошло это в 1896 году в Греции. За прошедшее столетие Олимпийские игры однажды проводились и в Москве. Узнайте в каком году это было. Для этого упростите выражение и найдите его значение при указанных значениях переменной :

• 2 ab (10b – 1) – (b – 6) x ab =
• Если a = 4; b. = 5;

2

Ответ : 2 ab (10b -1) – (b – 6) x ab =19ab + 4ab. Олимпийские игры проводились в Москве в 1980 году.

Упростите выражение и, используя данные таблицы и найденные ответы, узнайте :

• А) как назывались победители Олимпийских игр в древности :
• (x – 3) (x + 7) – (x + 5) (x – 1) =
• Б) как назывались судьи и распорядители игр :
• (x – 5) (x + 8) – (x + 4) (x - 1) =

-36

элладоники

8x -25

6x - 44

лауреаты

-44

атлеты

-16

чемпионы

олимпионики

25 – 8x

гоплиты

Ответ :

• А) Олимпионики ;
• Б) Элладоники ;

Представьте многочлен в стандартном виде и заполните таблицу буквами в соответствии с найденными ответами :

• C 13a – 5ab – 3ab =
• И 3 ab – 5 a -8 ba =
• Е 6 ab – 2b -6ba + 5a + 0 , 6b =
• X 2ab – 5ab +3ab – 8ba – 2ba =
• A -4a x ba +2ab + 0,2ab – 2ab =
• Л 3ab + 5a x 0,2ab – 4ab x 0,5b + 2ab =

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

3

2

2

2

2

- герой древнегреческой мифологии, участник Троянской войны. Какое крылатое выражение связано с именем этого героя ?

-1,8 ab – 2ab

3ab -13 ab

-5ab – 5a

ab +3ab

3ab +ab

5a – 1.4b

13a -8ab

2

2

2

2

2

3

2

2

2

2

3

2

2

Ответ : Ахиллес.

• Его мать, Фетида, окунула младенца в воды подземной реки, делающие человека неуязвимым. При этом погружении она держала Ахиллеса за пятку, которая осталась сухой и, следовательно, уязвимой. Во время Троянской войны стрела врага попала Ахиллесу в пятку, в результате чего он и умер.
• Выражение «Ахиллесова пятка» в переносном смысле означает «слабое, уязвимое место».

Долгое время одну из известных в древности планет в периоды утренней и вечерней видимости греки считали двумя разными светилами.

Упростите заданные алгебраические выражения. Зачеркните в таблице названия планет, связанные с найденными ответами. Оставшееся название позволит вам узнать, с какой планетой это заблуждение было связано.

(2 a – 1) – 4a =

4a (a -2) –(a -2) +4 =

(a +2) (a + 4) – (a + 1) =

(a – 1) – (a + 1) (a + 2) =

2

2

2

2

2

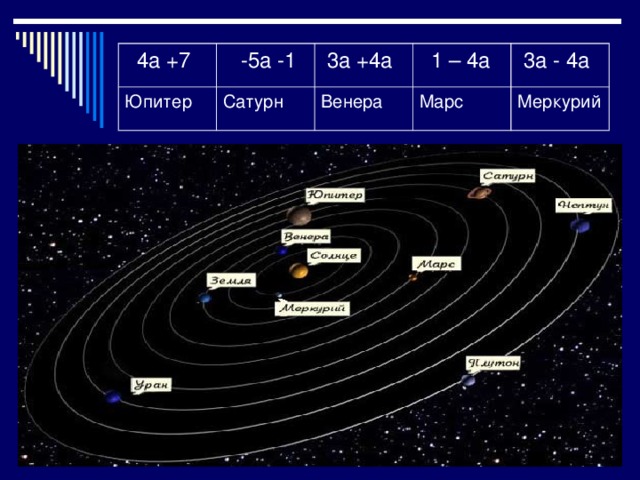
4a +7

-5a -1

Юпитер

3a +4a

Сатурн

1 – 4a

Венера

3a - 4a

Марс

Меркурий

Ответ : это планета Венера

В IV веке до н.э. греки дали планетам имена своих богов. Венера, например, вместо названия Фосфорос стала называться именем богини красоты Афродиты. Об этих новых названиях планет писал в своих работах Аристотель.

• Упростите алгебраические выражение. По совпадающим ответам соотнесите греческие названия планет с римскими, ныне используемыми.

2

• Арес : (х - 4) + 8 (х – 2) =
• Кронос : х + 4 – (х + 2) =
• Зевс : (х + 5) – х (х + 10) – 50 =
• Гермес : (х + 2) – (х – 2) =
• Сатурн : (4х – 5) – 4х (4х -9) – 25 =
• Меркурий : 4(х + 1) – 4 (1 – х) =
• Марс : (2х + 1) – (х + 1) (3х + 1) =
• Оставшееся греческое название - …….. – соответствует римскому, ныне употребляемому названию – Юпитер.

2

2

2

2

2

2

2

2

2

2

2

2

Ответ : римляне, перенявшие греческую культуру, просто перевели на свой язык имена планет, которые мы используем и сейчас.

• Гермес – Меркурий
• Арес – Марс
• Зевс – Юпитер
• Кронос – Сатурн

Преобразуйте произведения в многочлены стандартного вида и запишите в таблицу буквы, соответствующие найденным ответам :

2

2

• Е (х – у) (х + у) =
• А (2 – х) (х + 2) =
• М (2х +1) (1 – 2х) =
• Т (2х – у) (2х + у) =
• С (2х +3у) (2х – 3у) =
• К (х – 2) (2 + х ) =
• О (3х – 0,2у ) (0,2у +3х ) =
• И (2/3х + 0,5у) (0,5у – 2/3х ) =

9у – 4х

Х – у

1-4х

0,25у – 4/9х

9х – 0,04у

4х – у

0,25у – 4/9х

Х – 4

4 – х

2

2

2

2

2

4

4

2

2

2

2

2

2

2

2

2

6

3

3

4

2

Ответ :

2

2

9у – 4х

С

Х – у

Е

1-4х

М

0,25у – 4/9х

И

9х – 0,04у

О

4х – у

Т

0,25у – 4/9х

И

Х – 4

К

4 – х

А

2

2

2

2

2

4

4

2

2

6

2

4

2

• Э

Заполните пропуски :

• Полученное слово – « …..» - название науки о знаках.
• Вам уже известны некоторые знаки и символы, используемые в математике. Например, знак + обозначает ….. , знак % заменяет слово « ….. » , а знак - ….. .
• Использование знаков и символов дает возможность сделать записи более короткими и лаконичными.
• Аналогично, в других науках существуют свои условные обозначения.

Представьте выражение в виде многочлена. Запишите в таблицу буквы, соответствующие найденным ответам. Прочитайте слово. Что оно означает?

• Р (2х – 3) (2х + 3) =
• Г (2х + 3) (3 – 2х) =
• Л 3 – (3 – 2х) (3 + 2х) =
• Д (2х – 3) (2х – 3) =
• Ь (2х + 3) (-2х – 3) =
• Е (2х – 3) (3 – 2х) =
• К (2х + 3) (2х – 3) (4х +9) =
• И (2х – 3) – (2х + 3) =
• А (2х + 3) – (2х – 3) (2х + 3) =

2

2

2

2

Ответ

Буква

9 – 4х

-4х + 12х – 9

4х – 9

12х +18

4х – 6

-4х – 12х – 9

4х – 12х + 9

-24х

16х – 81

18 + 12х

2

2

2

2

2

2

4

Геральдика – наука о гербах

В настоящее время в денежном обороте находятся банкноты достоинством 5 , 10, 50, 100, 500 и 1000 рублей. Для художественного оформления банкнот используются изображения достопримечательностей городов России. Узнайте, какие это города и с банкнотами какого достоинства они связаны. Для этого выполните преобразования выражений и запишите результаты в стандартном виде. Используя найденные ответы как алгебраические коды, заполните таблицу названиями городов.

• Санкт-Петербург : (х – 2) (х + 2х + 4) =
• Красноярск : (1 + х) (х – х + 1) =
• Владивосток : х (1 – х) (1 + х + х ) =
• Архангельск : (х – 1) (х + 2х + 1) =
• Новгород : (х – 1) (х + 1) (х + х + 1) =
• Мурманск : (1 – х) (1 + х) (2 + 2х ) =
• Ярославль : (х + 3) (х + 9) – (х + 3) х 3х =

2

2

2

2

2

4

2

2

Достоинство

банкноты

Алгебраический код города

5 руб.

Название города

Х – 6

10 руб.

Х + 1

50 руб.

Х – 8

100 руб.

500 руб.

Х + х

Х – 2х + 1

1000 руб.

Х + 27

6

3

3

4

2

4

3

• Оставшаяся банкнота украшена достопримечательностями столицы России.
• Какого она года?
• Какое архитектурное сооружение на ней изображено?
• По проекту какого архитектора оно построено?

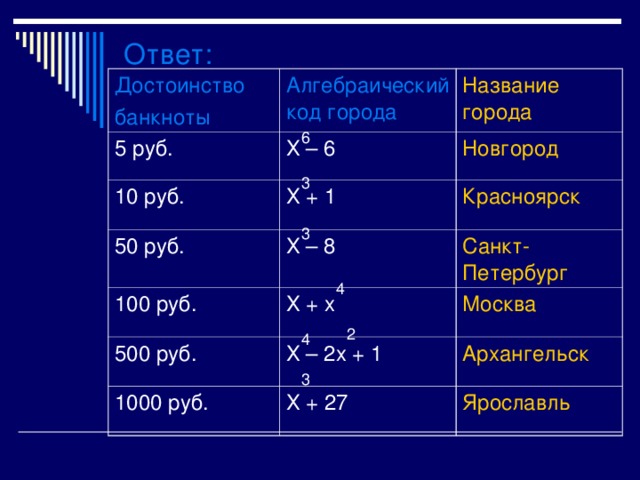
Ответ :

Достоинство

банкноты

Алгебраический код города

5 руб.

Название города

Х – 6

10 руб.

Новгород

Х + 1

50 руб.

Красноярск

Х – 8

100 руб.

500 руб.

Х + х

Санкт-Петербург

Х – 2х + 1

1000 руб.

Москва

Архангельск

Х + 27

Ярославль

6

3

3

4

2

4

3