Презентация по теме "Подобие треугольников"

Геометрия

глава 7

Подобные треугольники.

Подготовила Намазгулова Гульназ ученица 8б класса ГБОУ РПЛИ г.Кумертау

Учитель: Баянова Г.А.

Подобные треугольники

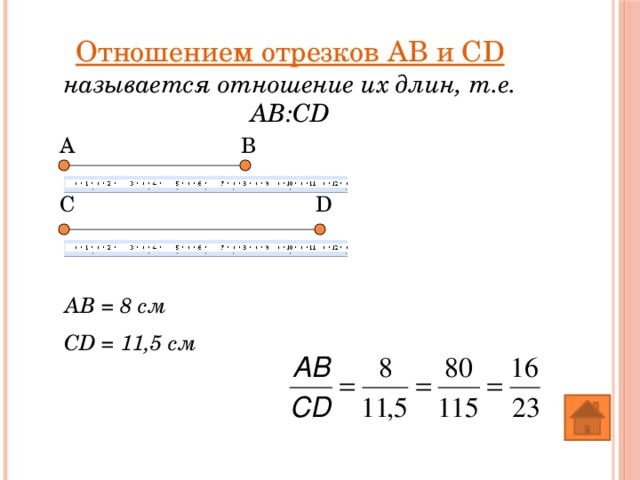
Отношением отрезков АВ и СD называется отношение их длин, т.е. АВ:CD

В

А

С

D

АВ = 8 см

СD = 11,5 см

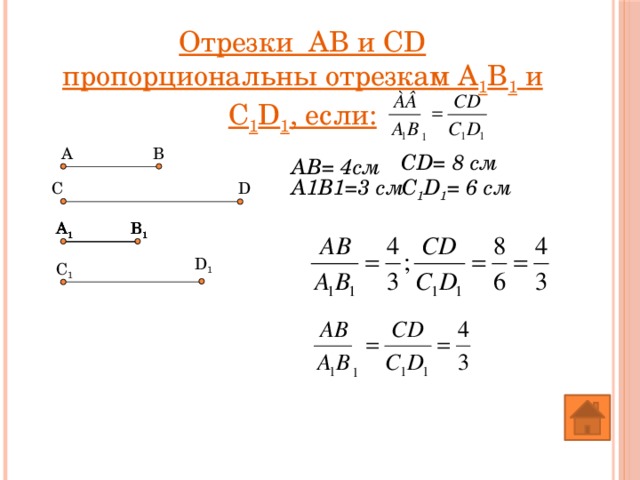
Отрезки АВ и CD пропорциональны отрезкам А 1 В 1 и С 1 D 1 , если:

В

А

CD= 8 см

АВ= 4см

С 1 D 1 = 6 см

А1В1=3 см

D

С

В 1

A 1

В 1

В 1

A 1

A 1

В 1

A 1

D 1

С 1

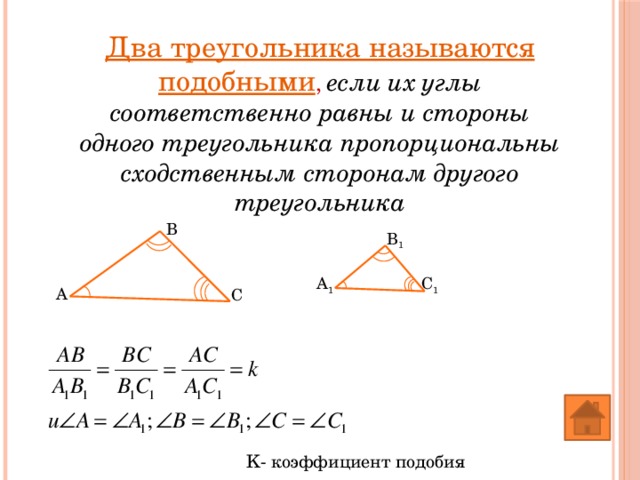
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника

B

B 1

A 1

C 1

A

C

K- коэффициент подобия

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия

B

B 1

Доказательство:

A 1

C 1

A

C

,коэффициент подобия равен К

Пусть

S и S 1 - площади треугольников, то

По формуле имеем

и

Поэтому

Признаки подобия треугольников

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны

Доказать:

Дано:

В

В 1

С 1

С

А 1

А

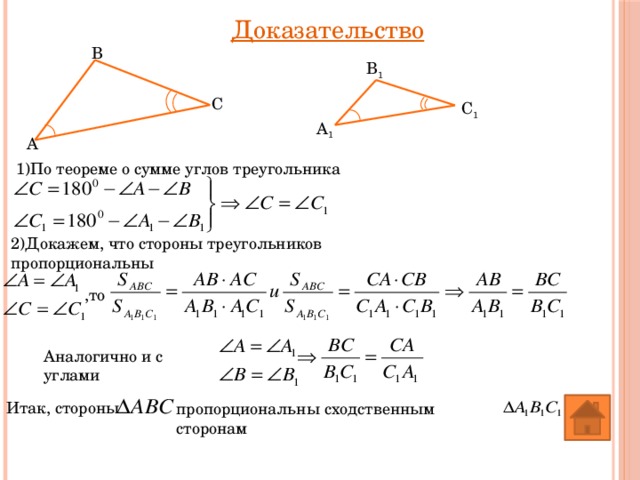
Доказательство

В

В 1

С

С 1

А 1

А

1)По теореме о сумме углов треугольника

2)Докажем, что стороны треугольников пропорциональны

,то

Аналогично и с углами

Итак, стороны

пропорциональны сходственным сторонам

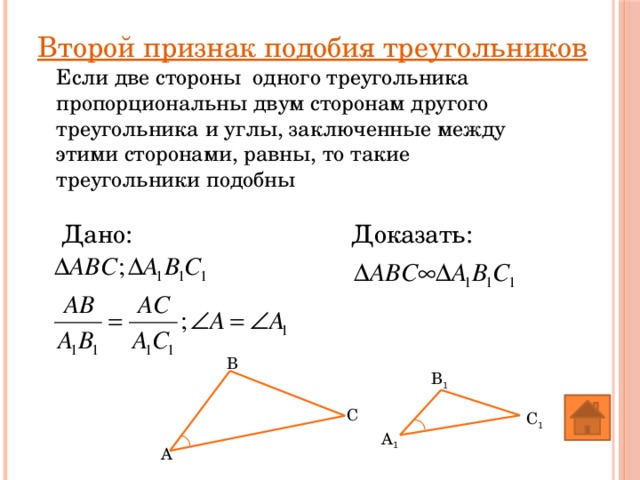
Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны

Доказать:

Дано:

В

В 1

С

С 1

А 1

А

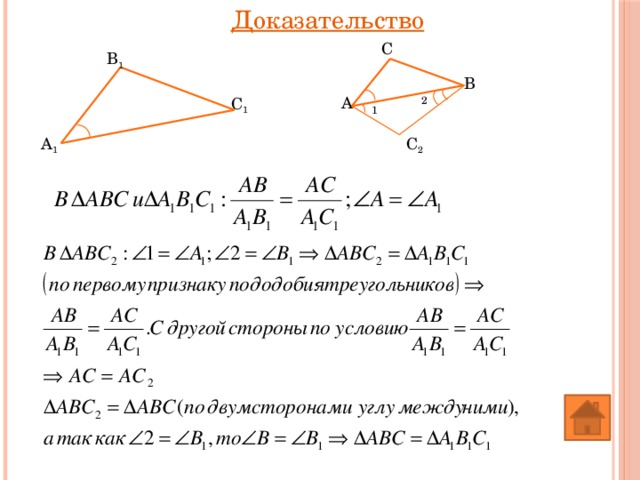
Доказательство

С

В 1

В

А

2

С 1

1

С 2

А 1

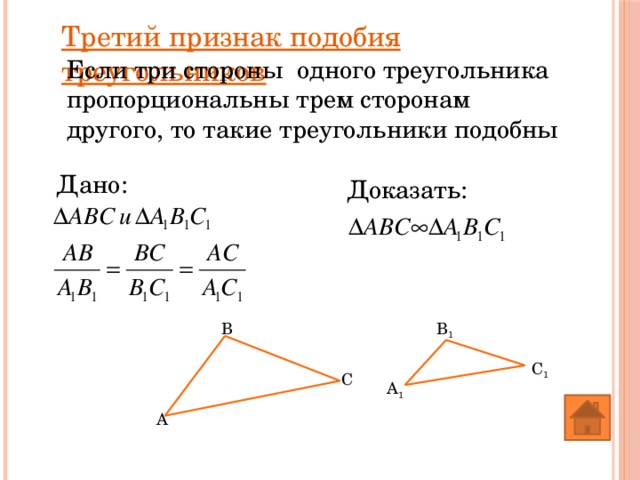
Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны

Дано:

Доказать:

В

В 1

С 1

С

А 1

А

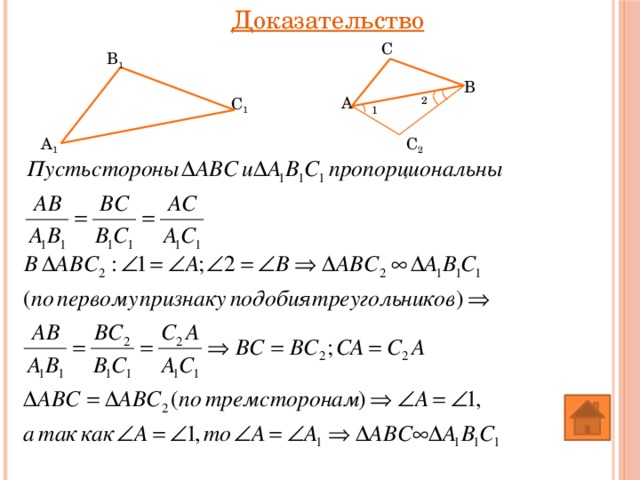
Доказательство

С

В 1

В

А

С 1

2

1

С 2

А 1

Применение подобия к доказательству теорем и решению задач

Средней линией называется отрезок, соединяющий середины двух его сторон

Теорема:

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны

Дано:

Доказать:

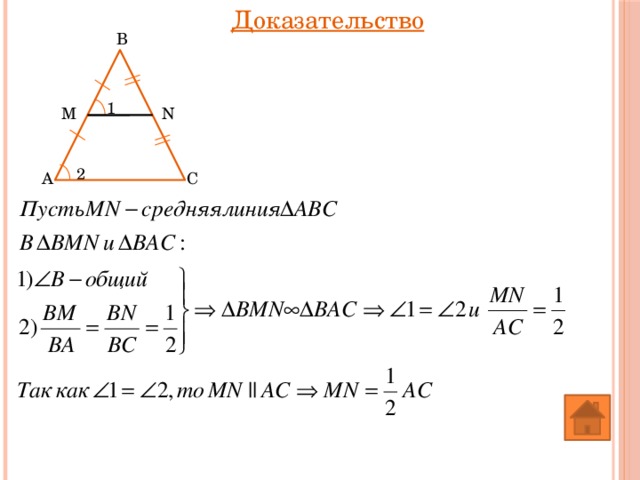
Доказательство

В

1

M

N

2

С

А

Теорема:

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины

Доказать:

Дано:

C

B 1

A 1

O

B

A

C 1

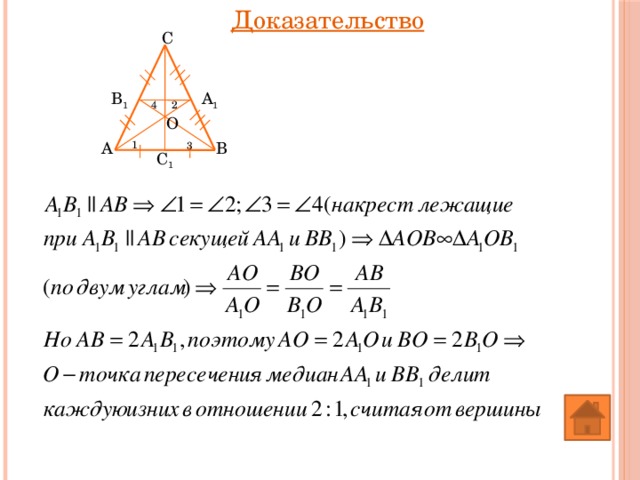
Доказательство

C

B 1

A 1

2

4

O

B

A

1

3

C 1

Теорема:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику

Доказать:

Дано:

Доказательство

C

A

B

D

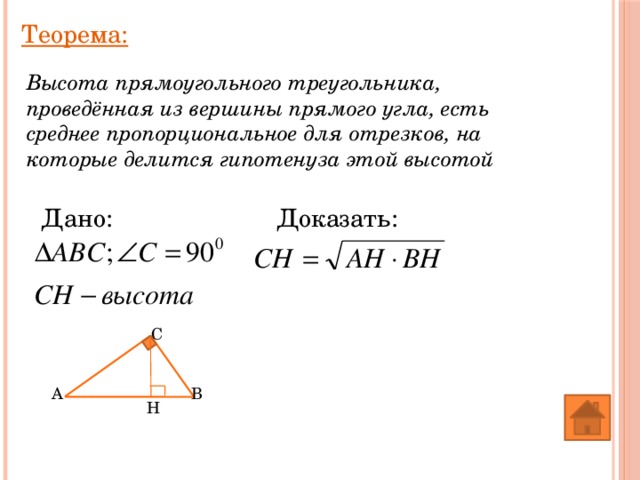
Теорема:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой

Доказать:

Дано:

C

A

B

H

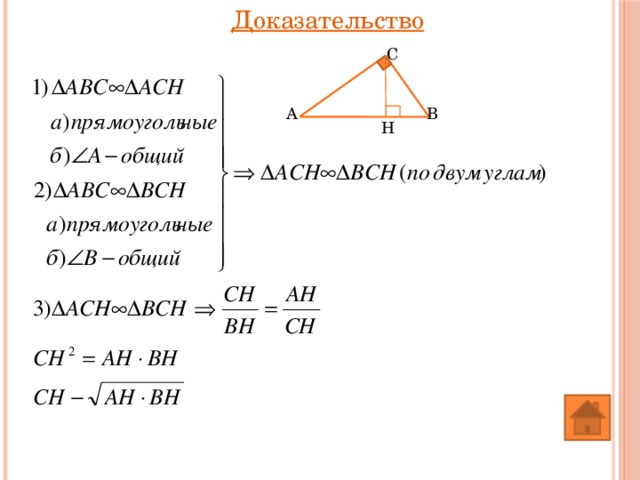
Доказательство

C

A

B

H

Синус, косинус и тангенс острого угла прямоугольного треугольника

В

Синус - отношение противолежащего катета к гипотенузе в прямоугольном треугольнике

А

С

Косинус - отношение прилежащего катета к гипотенузе в прямоугольном треугольнике

Тангенс- отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике

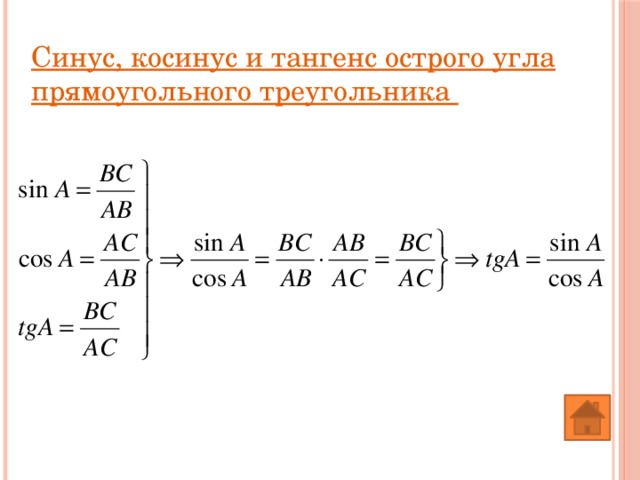
Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30 0 , 45 0 , 60 0

В

60 0

30 0

А

С

Дано:

Решение:

Значение синуса, косинуса и тангенса для углов 30 0 , 45 0 , 60 0

В

45 0

45 0

А

С

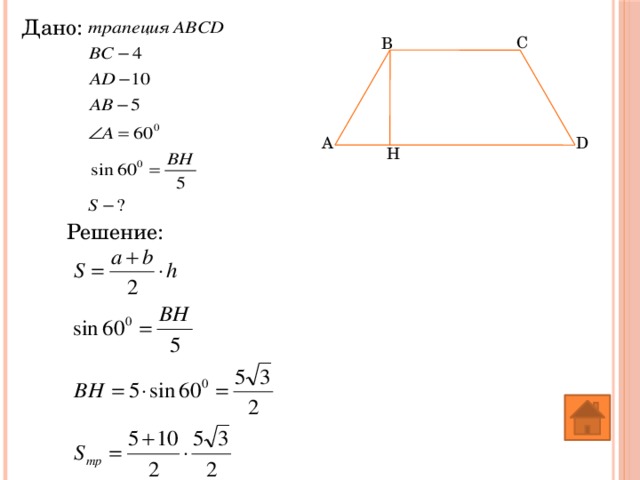
Дано:

С

В

D

А

H

Решение:

Конец