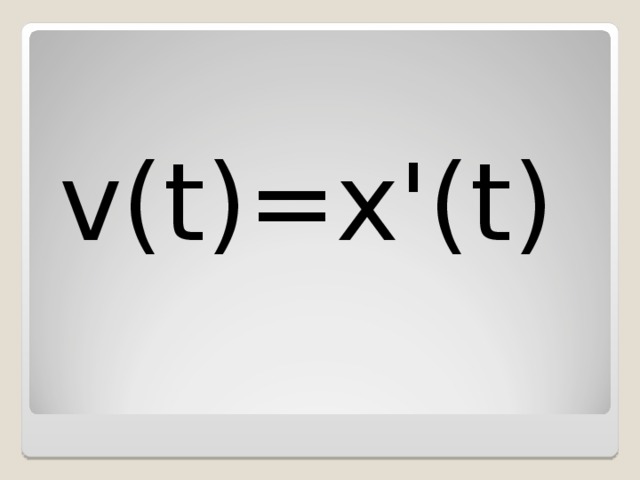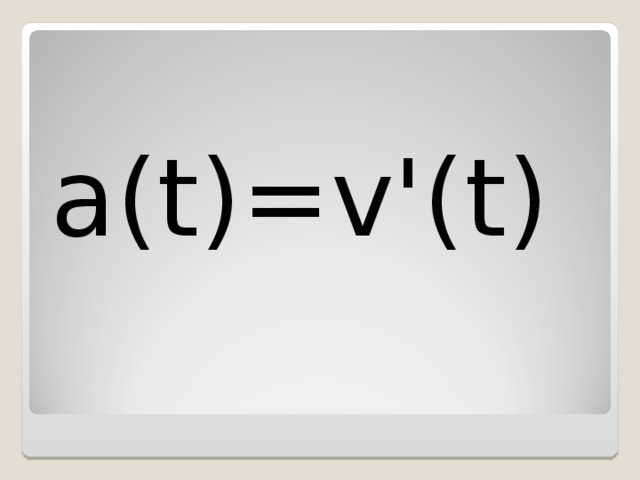Презентация урока "Применение производной"

Знания таблицы и правил – это надежный шаг к решению многих задач. Знайте производную !

Математическая разминка

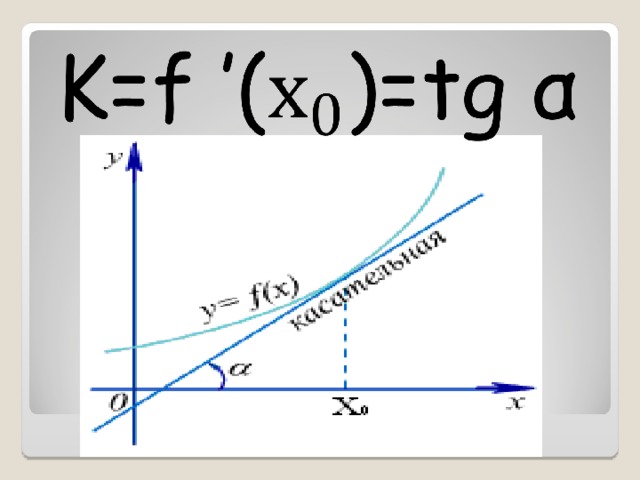
Геометрический смысл производной:

, где k – угловой коэффициент

касательной.

Физический смысл производной

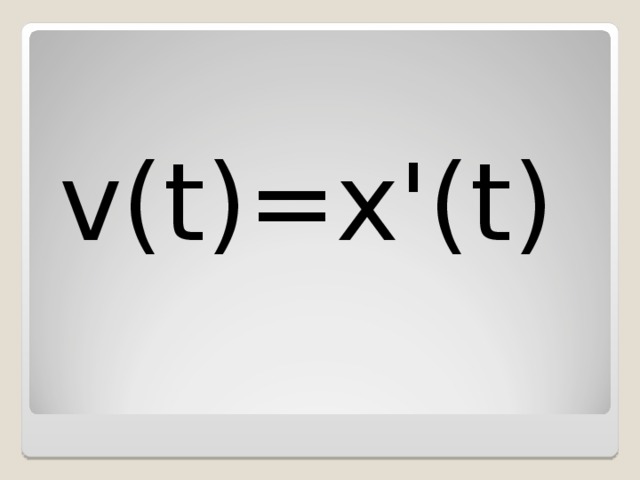
v ( t )= x '( t )

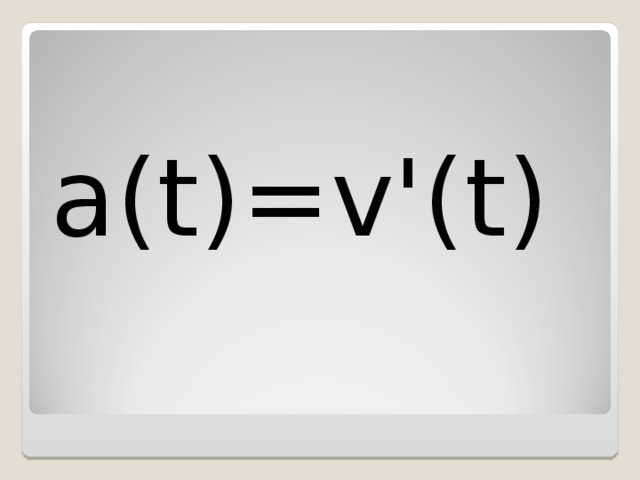
a ( t )= v '( t )

Производная – это скорость роста функции.

1. Мощность – это производная работы по времени

P (t) = A' (t).

2. Сила тока – производная от заряда по времени

I (t) = g' (t).

3. Сила – есть производная работы по перемещению

F (x) = A' (x).

4. Теплоемкость – это производная количества теплоты по температуре C (t) = Q' (t).

5. Давление – производная силы по площади

P (S) = F'(S)

6. Длина окружности – это производная площади круга по радиусу l окр (R) = S' кр (R).

7. Темп роста производительности труда – это производная производительности труда по времени.

8. Успехи в учебе? Производная роста знаний.

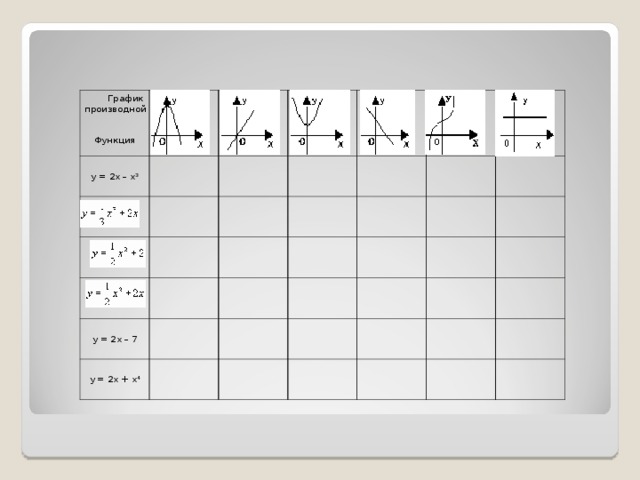
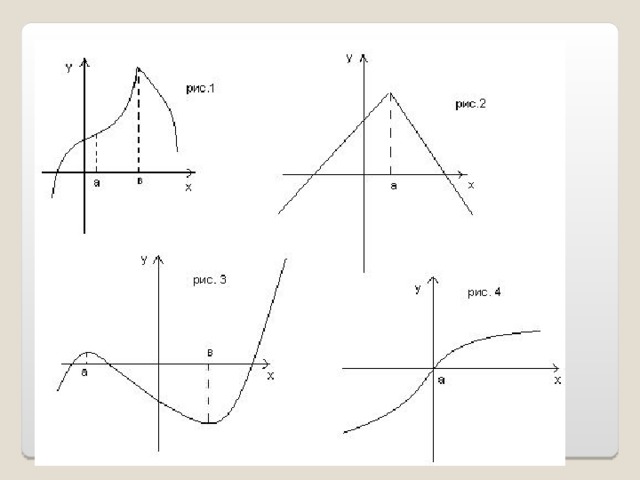
График производной

Функция

у = 2х – х 3

у = 2х – 7

у = 2х + х 4

Применение производной к исследованию функции

1) промежутки возрастания,

убывания

2) точки экстремума и значение

функции в этих точках

3) наибольшее и наименьшее

значение функции

4) построение графика функции

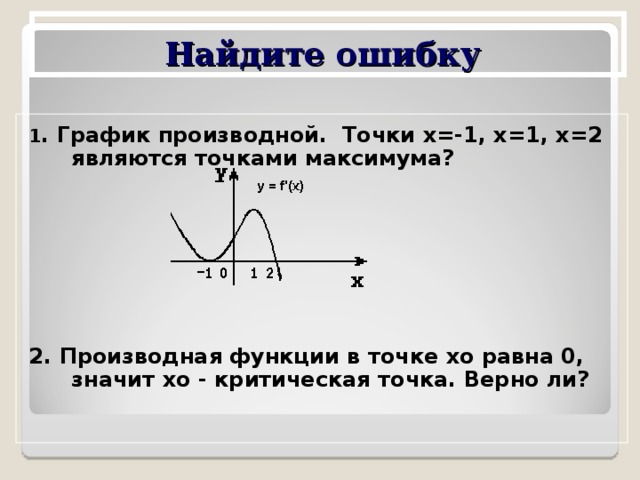
Найдите ошибку

1 . График производной. Точки х=-1, х=1, х=2 являются точками максимума?

2. Производная функции в точке хо равна 0, значит хо - критическая точка. Верно ли?

3. Критическая точка является точкой экстремума. Верно ли?

4. Точка экстремума является критической точкой. Верно ли?

Беспрепятственно решать любые примеры, связанные с производной, Вам помогут выполнение домашних заданий и самостоятельных работ на уроке.

Бак 2016

Работа в группах

Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно оградить бычьей шкурой. Но хитрая финикийская царица Дидона разрезала эту шкуру на ремешки, связала их и оградила ремнем большой участок земли, примыкавший к морю. Считая берег моря прямолинейным, а огражденный участок прямоугольным, перед Дидоной встала задача: как оградить прямоугольный участок имеющимися ремешками длиной  l , чтобы площадь была наибольшей?

Домашнее задание

Продолжи фразу:

«Сегодня на уроке я узнал(а) …»

«Сегодня на уроке я познакомился(ась ) …»

«Сегодня на уроке я повторил(а ) …»

«Сегодня на уроке я закрепил(а) …»

«Сегодня на уроке мне понравилось …»

Подведение итогов

Резерв

В конце урока учащиеся будут способны:

Ц1: вычислять производные элементарных и

сложных функций;

Ц2: распознавать и применять правила вычисления

производных при решении различных задач;

Ц3: решать задачи с применением уравнения

касательной к графику функций ;

Ц4: использовать приобретенные знания и умения в

практической деятельности для решения

геометрических и физических задач;

Цели урока: