Приложение 5.2 к Обобщению опыта

Математика 9 класс 1 полугодие 1 вариант

1. О числах а и с известно, что a c. Какое из следующих неравенств неверно?

1) a – 3 4)

1. Укажите неравенство, соответствующее рисунку:

1 ) -10

3) 4)

1. Решите неравенство 6 – 3х 26 – х .

1) x -10 2) x -3 4) x

1. По графику квадратичной функции у = ах² + bx + c определите знаки коэффициентов а и с.

1) a

2) a 0

3) a 0, c

4) a 0, c 0

1. Найдите на рисунке график функции у = (х – 2)².

1) 2) 3) 4)

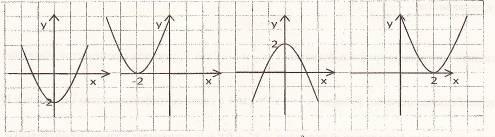
1. Определите, какое из данных чисел является корнем уравнения

х²(х + 1) + (х + 4) = 4

1) -1 2) 0 3) 1 4) 2

Математика 9 класс 1 полугодие 1 вариант

1. О числах а и с известно, что a c. Какое из следующих неравенств неверно?

1) a – 3 4)

1. Укажите неравенство, соответствующее рисунку:

1 ) -10

3) 4)

1. Решите неравенство 6 – 3х 26 – х .

1) x -10 2) x -3 4) x

1. По графику квадратичной функции у = ах² + bx + c определите знаки коэффициентов а и с.

1) a

2) a 0

3) a 0, c

4) a 0, c 0

1. Найдите на рисунке график функции у = (х – 2)².

1) 2) 3) 4)

1. Определите, какое из данных чисел является корнем уравнения

х²(х + 1) + (х + 4) = 4

1) -1 2) 0 3) 1 4) 2

1. Изобразив схематически графики, выясните сколько решений имеет система уравнений

1) 0 2) 1 3) 2 4) 3

1. Какое из неравенств не имеет решения?

1) x² – 1 0 2) x² + 1 0 3) x² – 1 ² + 1

1. Найдите координаты вершины параболы у = -0,5х² + 3х – 4.

2. Решите систему уравнений

3. Решите задачу. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

1. Изобразив схематически графики, выясните сколько решений имеет система уравнений

1) 0 2) 1 3) 2 4) 3

1. Какое из неравенств не имеет решения?

1) x² – 1 0 2) x² + 1 0 3) x² – 1 ² + 1

1. Найдите координаты вершины параболы у = -0,5х² + 3х – 4.

2. Решите систему уравнений

3. Решите задачу. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

Математика 9 класс 1 полугодие 2 вариант

1. О числах m и n известно, что m n. Какое из следующих неравенств неверно?

1) m – 5 n – 5 2) m + 3 n + 3 3) 4)

1. Укажите неравенство, соответствующее рисунку:

1 ) -1

3) 4)

1. Решите неравенство 1 – 2х 5 .

1) x -2 2) x 2 4) x

1. По графику квадратичной функции у = ах² + bx + c определите знаки коэффициентов а и с.

1) a

2) a 0

3) a 0, c

4) a 0, c 0

1. Найдите на рисунке график функции у = х² – 2.

1) 2) 3) 4)

1. Определите, какое из данных чисел является корнем уравнения

х²(х - 7) + 7(х² – x) = -6

1) -1 2) 0 3) 1 4) -2

Математика 9 класс 1 полугодие 2 вариант

1. О числах m и n известно, что m n. Какое из следующих неравенств неверно?

1) m – 5 n – 5 2) m + 3 n + 3 3) 4)

1. Укажите неравенство, соответствующее рисунку:

1 ) -1

3) 4)

1. Решите неравенство 1 – 2х 5 .

1) x -2 2) x 2 4) x

1. По графику квадратичной функции у = ах² + bx + c определите знаки коэффициентов а и с.

1) a

2) a 0

3) a 0, c

4) a 0, c 0

1. Найдите на рисунке график функции у = х² – 2.

1) 2) 3) 4)

1. Определите, какое из данных чисел является корнем уравнения

х²(х - 7) + 7(х² – x) = -6

1) -1 2) 0 3) 1 4) -2

1. Изобразив схематически графики, выясните сколько решений имеет система уравнений

1) 0 2) 1 3) 2 4) 3

1. Какое из неравенств верно при любом значении х ?

1) x² – 1 0 2) x² + 1 0 3) x² – 1 ² + 1

1. Найдите координаты вершины параболы у = 0,5х² + 2х – 2.

1. Решите систему уравнений

2. Решите задачу. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

1. Изобразив схематически графики, выясните сколько решений имеет система уравнений

1) 0 2) 1 3) 2 4) 3

1. Какое из неравенств верно при любом значении х ?

1) x² – 1 0 2) x² + 1 0 3) x² – 1 ² + 1

1. Найдите координаты вершины параболы у = 0,5х² + 2х – 2.

1. Решите систему уравнений

2. Решите задачу. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.