Признаки параллелограмма

Геометрия 8 класс

Дата

Урок № 11

Тема: Признаки параллелограмма

Цель: закрепить свойства и признаки параллелограмма в процессе решения задач; совершенствовать навыки решения задач.

УУД

Личностные: Создание условий к саморазвитию и самообразованию; формирование положительной учебной мотивации, понимание смысла учебной деятельности.

Регулятивные: Формулировать тему и цель урока с помощью учителя; учить высказывать своё предположение на основе материала учебника.

Познавательные: умение самостоятельно находить и структурировать информацию, грамотно формулировать свои мысли.

Коммуникативные: Формировать умение делать выводы из прочитанного; формировать умение слушать товарищей и высказывать своё мнение.

Предметные: формулировать определение параллелограмма; формулировать свойства и признаки параллелограмма, применять свойства и признаки параллелограмма при решении задач

Тип урока: урок применения знаний и умений.

Ход урока

1. Организационный момент

2. Мотивация обучения. Сообщение темы и целей урока

3. Актуализация опорных знаний

Теоретический опрос

1.Дайте определение параллелограмма.

2. Перечислите свойства параллелограмма

3. Перечислите признаки параллелограмма

1. Решение задач

1. Точки Е и К – середины сторон АВ и CD параллелограмма ABCD. Докажите, что АЕСК – параллелограмм.

2. Диагонали четырехугольника ABCD пересекаются в точке О, причем АС = 2 дм, АО = 10 см, BD = 1,5 дм, ВО = 7 см. Выясните, является ли ABCD параллелограммом?

3. В параллелограмме ABCD на сторонах АВ и CD отмечены соответственно точки М и N так, что ∠BMC = ∠AND. Докажите, что AMCN – параллелограмм.

4. Точки А и В делят диагональ МК параллелограмма MNKP на три равные части. Является ли четырехугольник ANBP параллелограммом? Ответ обоснуйте.

четырёхугольник MBND параллелограммом? Ответ обоснуйт

5. Дано: ABCD – параллелограмм, AM = СК, АР = CN (рис. 5.52). Доказать: MNKP – параллелограмм.

6. Через точку пересечения диагоналей О параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и ВС в точках М и N соответственно. Является ли MBND параллелограммом? Ответ обоснуйте.

Решение задач по готовым чертежам.

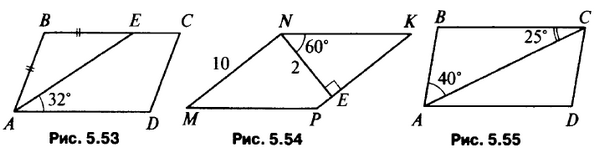
1. Дано: ABCD – параллелограмм (рис. 5.53). Найти: ∠C, ∠D.

2. Дано: MNKP – параллелограмм (рис. 5.54). Найти: МР, РК.

3. Рис. 5.55. Найти: углы параллелограмма ABCD.

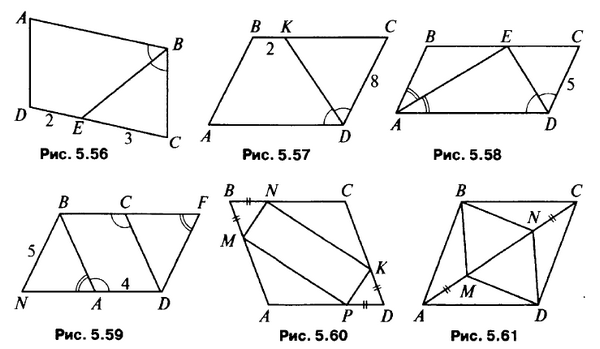
4. Дано: ABCD – параллелограмм (рис. 5.56). Найти: Р_ABCD.

5. Дано: ABCD – параллелограмм (рис. 5.57). Найти: AD.

6. Дано: ABCD – параллелограмм (рис. 5.58). Найти: P_ABCD, ∠AED.

7. Дано: NBFD – параллелограмм. AD = 4 см, NB = 5 см (рис. 5.59). Найти: ВС, CD.

8. Дано: ABCD – параллелограмм. P_MNKP = 20 см (рис. 5.60). Найти: MN, МР.

9. Дано: BNDM – параллелограмм. АВ : ВС = 4:5, P_ABCD = 18 см (рис. 5.61). Найти: AD, DC.

1. Итоги урока. Рефлексия

1. Дано: ABCD – параллелограмм (рис. 5.53). Найти: ∠C, ∠D.

2. Дано: MNKP – параллелограмм (рис. 5.54). Найти: МР, РК.

3. Рис. 5.55. Найти: углы параллелограмма ABCD.

4. Дано: ABCD – параллелограмм (рис. 5.56). Найти: Р_ABCD.

5. Дано: ABCD – параллелограмм (рис. 5.57). Найти: AD.

6. Дано: ABCD – параллелограмм (рис. 5.58). Найти: P_ABCD, ∠AED.

7. Дано: NBFD – параллелограмм. AD = 4 см, NB = 5 см (рис. 5.59). Найти: ВС, CD.

8. Дано: ABCD – параллелограмм. P_MNKP = 20 см (рис. 5.60). Найти: MN, МР.

9. Дано: BNDM – параллелограмм. АВ : ВС = 4:5, P_ABCD = 18 см (рис. 5.61). Найти: AD, DC.

1. Дано: ABCD – параллелограмм (рис. 5.53). Найти: ∠C, ∠D.

2. Дано: MNKP – параллелограмм (рис. 5.54). Найти: МР, РК.

3. Рис. 5.55. Найти: углы параллелограмма ABCD.

4. Дано: ABCD – параллелограмм (рис. 5.56). Найти: Р_ABCD.

5. Дано: ABCD – параллелограмм (рис. 5.57). Найти: AD.

6. Дано: ABCD – параллелограмм (рис. 5.58). Найти: P_ABCD, ∠AED.

7. Дано: NBFD – параллелограмм. AD = 4 см, NB = 5 см (рис. 5.59). Найти: ВС, CD.

8. Дано: ABCD – параллелограмм. P_MNKP = 20 см (рис. 5.60). Найти: MN, МР.

9. Дано: BNDM – параллелограмм. АВ : ВС = 4:5, P_ABCD = 18 см (рис. 5.61). Найти: AD, DC